Chiffre de Hill Chiffre de Hill Chiffrement CMi




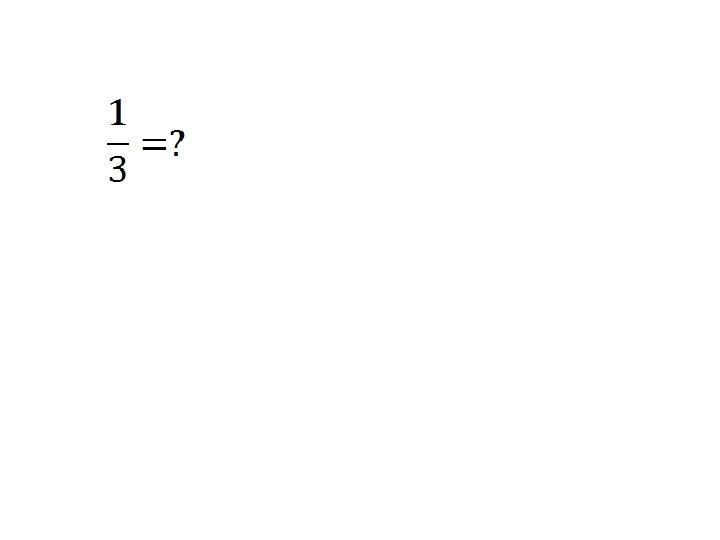
















- Slides: 22

Chiffre de Hill

Chiffre de Hill Chiffrement: C(Mi)= A. Mi Déchiffrement: Mi= A-1. C(Mi)

Chiffre de Hill Le chiffre de Hill est une méthode de cryptage symétrique qui utilise certaines propriétés du calcul matriciel.

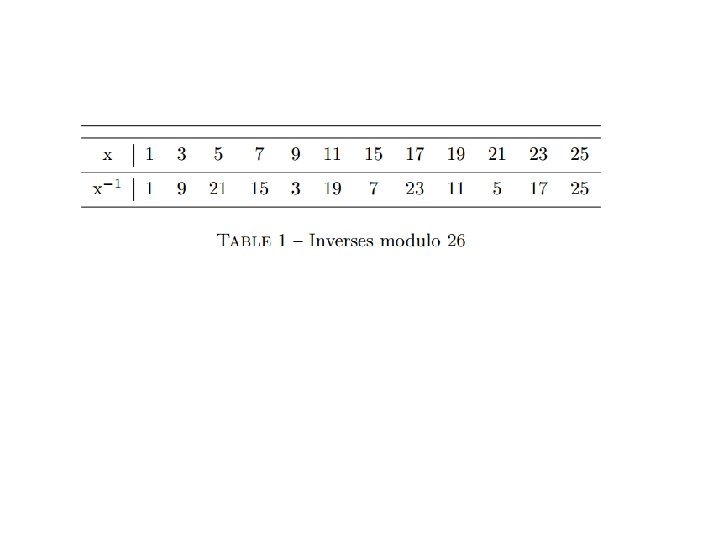
Z 26 : Les nombres de 0 à 25 (ensemble des restes modulo 26) Si lors des calculs certains résultats sont négatifs ou supérieurs à 25, les résultats seront ramenés à cet intervalle via l’opération de modulo 26 On dit que i est inversible dans Z 26 s’il existe j dans Z 26 tel que (i x j) mod 26 = 1 dans Z 26
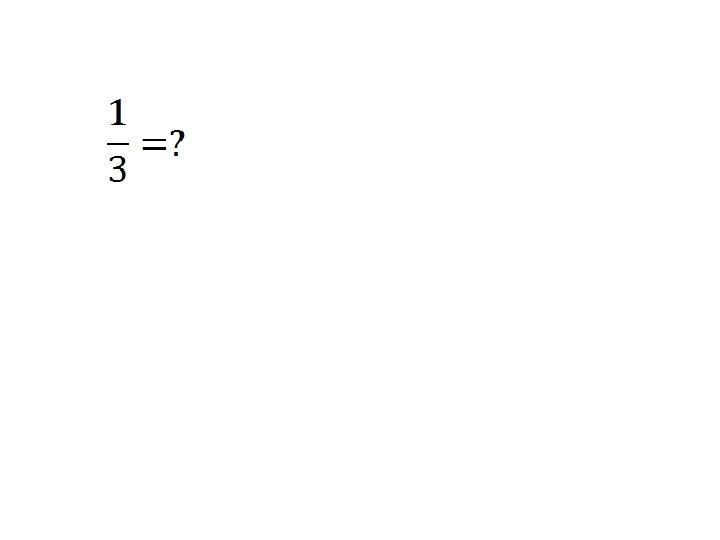


Rappels de calcul matriciel:

On dit qu’une matrice A est inversible dans Z 26 si Det(A) possède un inverse dans Z 26 L’inverse de Det(A) est noté Det(A)-1 La matrice inverse de A notée (A) -1 est obtenue de la façon suivante : (A)-1=t(com(A)) * Det(A)-1

L’encodage du message A B C D E F G H I J K L M N O P Q R S T U V WX Y Z 0 1 2 3 4 5 6 7 8 9. . . . 25 par exemple Lettre se code 11 4 19 19 17 4 . Le message m est séparé en bloc de 2 lettres pour être encrypté.

Fonctionnement: Soit une matrice inversible Pour chiffrer chaque paire d’un message M notée Mi , il suffit d’appliquer une multiplication de matrice : C(Mi)= A. Mi (mod 26) Pour déchiffrer un message chiffré avec la matrice A, on utilise la matrice inverse A-1 Mi= A-1. C(Mi) (mod 26)

Exemple Calculer Det(A) = ? Det(A) = 13 *13 - 10*24 = 7. Puisque 7 a pour inverse 15 modulo 26 : (7 *15) mod 26 = 1 , la matrice A est inversible et peut donc nous servir à crypter nos messages. (A)-1=t(com(A)) * Det(A)-1 Calculer: (A)-1=?

Crypter le message "BC" Son encodage numérique est : Déchiffrement:

Exemple 2 chiffrer le message suivant : TEXTEACRYPTER en utilisant une matrice A

Solution: Det(A)=21 Comme 5 × 21 = 105 et 105 mod 26=1 Donc, 5 est un inverse de det(A) modulo 26. • on code le message TEXTEACRYPTER→ 19 ; 4 ; 23 ; 19 ; 4 ; 0 ; 2 ; 17 ; 24 ; 15 ; 19 ; 4 ; 17

On regroupe les lettres par paires créant ainsi 7 vecteurs de dimension deux, la dernière paire étant complétée arbitrairement : On multiplie ensuite ces vecteurs par la matrice A (modulo 26 ) On obtient alors 7 vecteurs, soit 14 lettres : ZAITMYNPRJZADW.

Déchiffrement = 5 a=qd+r (A)-1 = 30=26 x 1+4 Connaissant les couples Y, il suffit de les multiplier (modulo 26) par la matrice (A)-1 pour retrouver les couples X et réussir à déchiffrer le message.

ØPGCD ØThéorème de Bézout

• Calculons, par exemple, le PGCD de 1071 et de 1029 à l'aide de l'algorithme d'Euclide : a = qb + r • 1071 = 1029 × 1 + 42 • 1029 = 42 × 24 + 21 • 42 = 21 × 2 + 0 • Il faut prendre le dernier reste avant le zéro, donc PGCD(1071 ; 1029) = 21

• Théorème de Bézout • Le théorème de Bézout affirme que le PGCD de deux entiers a et b est une combinaison linéaire (à coefficients entiers) de a et b : au + bv= pgcd(a, b). (il existe des entiers u et v ) Une modification simple de l'algorithme d'Euclide (qu'on appelle alors algorithme d'Euclide étendu) permet de calculer ces coefficients u et v.

• Calcul des coefficient de Bézout pour a= 600 et b=124 600=124 x 4 +104 124=104 x 1 + 20 104= 20 x 5 + 4 20 = 4 x 5 +0 = 600 x 6 + 124 x (-29) = 124 x (-5)+ (600 - 124 x 4) x 6 =124 x (-5)+ 104 x 6 = 104 -(124 -104 x 1) x 5 4 =104 – 20 X 5

Deux nombres entiers sont dits premiers entre eux lorsqu'il n'admette aucun diviseur commun, sinon l'unité. De manière équivalente, deux nombres entiers a et b sont premiers entre eux lorsque la fraction a/b est irréductible

Lorsque deux entiers a et n sont premiers entre eux, on sait qu'il existe deux nombres u et v tels que au + nv = 1. Modulo n, cette égalité devient au = 1 (mod n). Le nombre u est tel que son produit modulo n avec a donne 1. Autrement dit, si a et n sont premiers entre eux, alors a possède un « inverse » modulo n.