Chi Squared Test Why Chi Squared To test

Chi Squared Test

Why Chi Squared? • To test to see if, when we collect data, is the variation we see due to chance or due to something else?

• This is the Chi Squared Test Formula • Greek letter “X” is “Chi” • Don’t get confused- X 2 is the name of the whole variable- you don’t have to ever take the square root of it or solve for X.

Coin Flipping Example • If you flip a coin 100 times and get this data: • 62 Heads • 38 Tails • The question we wonder about this data: • Is this due to chance? Or. . . • Is this not due to chance? • For example: • Perhaps there something wrong with • the coin? • Perhaps there is something wrong with the way I am flipping the coin, etc. ? Chi Squared test lets us answer this!!

Null Hypothesis • The Chi Squared Test begins with the Null Hypothesis • The Null Hypothesis says: There is no significant statistical difference between the observed and expected frequencies (i. e. the differences we see are simply due to chance). • For a coin flipping experiment: • The expected values are 50 heads, 50 tails. • The observed values are 62 heads, 38 tails. • Question we are trying to answer: are the observed values due to chance or. . . not

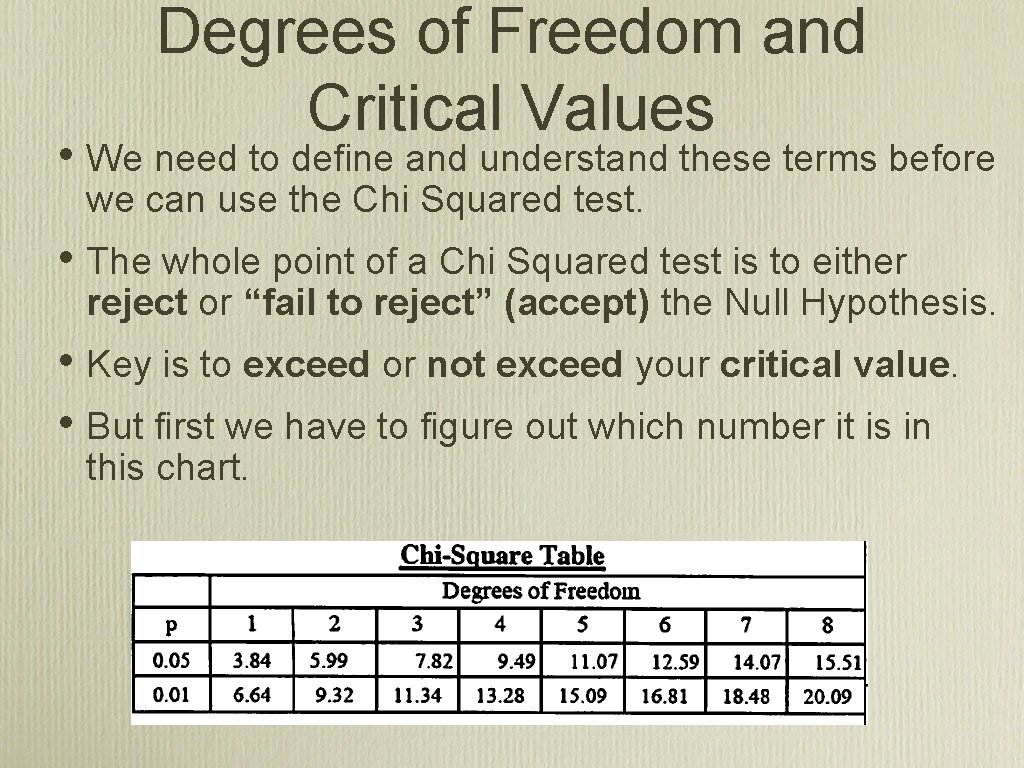
Degrees of Freedom and Critical Values • We need to define and understand these terms before we can use the Chi Squared test. • The whole point of a Chi Squared test is to either reject or “fail to reject” (accept) the Null Hypothesis. • Key is to exceed or not exceed your critical value. • But first we have to figure out which number it is in this chart.

Degrees of Freedom • Because we are comparing outcomes, we need at least two outcomes in our experiment. • We are flipping coins so we have two outcomesheads or tails. • To get degrees of freedom we simply subtract one from the two possible outcomes. 2 -1= 1 • Therefore, in this experiment we have 1 degree of freedom

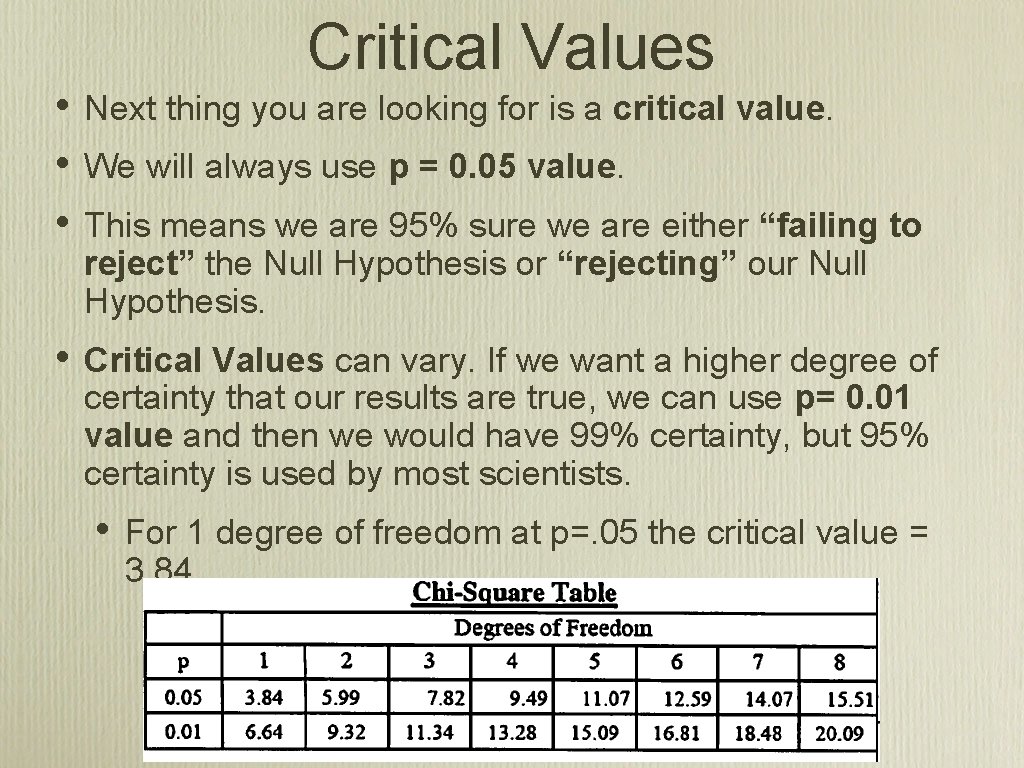
Critical Values • • • Next thing you are looking for is a critical value. • Critical Values can vary. If we want a higher degree of certainty that our results are true, we can use p= 0. 01 value and then we would have 99% certainty, but 95% certainty is used by most scientists. We will always use p = 0. 05 value. This means we are 95% sure we are either “failing to reject” the Null Hypothesis or “rejecting” our Null Hypothesis. • For 1 degree of freedom at p=. 05 the critical value = 3. 84.

• Null Hypothesis says: • There is no significant statistical difference between the observed and expected frequencies (i. e. the differences we see are simply due to chance). • • Null Hypothesis We either reject or “fail to reject” (accept) the null hypothesis. • Reject the Null Hypothesis: This means there is a statistical difference between the observed and expected frequencies • Fail to Reject (accept) the Null Hypothesis: This means there is no statistical difference between the observed and expected frequencies In this case the critical value is 3. 841 • If your Chi Squared is greater than 3. 841 you reject the Null Hypothesis • • Therefore, there is something aside from chance that is causing us to get more heads than tails. If your Chi Squared is less than 3. 841 you “fail to reject” (accept) the Null Hypothesis. • This is usually what happens unless you have something that is

• • • Practice- Coin Toss 50 tosses • Expected: Heads: 25 Tails: 25 • Observed: Heads: 28 Tails: 22 Do it for heads Do it for tails What is our Critical Value? • 2 -1 = 1 • 3. 84 If our Chi Squared is greater than the critical value we reject our Null Hypothesis If our Chi Squared is less than the critical value we “fail to reject” (accept) our Null Hypothesis • This means there is no statistical significance between what we observed & what we expected. What we got is due to chance- nothing’s weird about the coins

• Practice- Dice 36 dice • Expected: 6 of each • Observed:

Practice- Dice • • Chi Squared Degrees of Freedom • 6 -1=5 • Critical Value: 11. 07 • “Fail to reject” (accept) the Null Hypothesis • No difference between obs and exp • What we see is due to chance!