Chemistry Calculations Unit 1 Lesson 4 Topics Identifying

Chemistry Calculations Unit 1 Lesson 4

Topics • Identifying and Counting Sig. Figs • Rules for calculating with Sig. Figs – Adding or subtracting – Multiplying or dividing – Combined mathematical operations – Rules for rounding • Review of essential algebra for chemistry

Learning Goals By the end of this lesson, students will be able to • 1. Identify and count significant figures in a measurement • 2. Get EXACTLY the right answer in a calculation by obeying the rules for sig figs and rounding when adding, subtracting, multiplying, or dividing #s in standard form and/or scientific notation • 3. Perform basic algebraic processes including cross multiplying, rearranging equations, multiplying fractions, and performing unit conversions

Significant Figures (Significant Digits) • When looking at a recorded measurement, “significant figures” include all the measured digits + the 1 st estimated digit. • Sometimes, zeros are inserted before or after the decimal point as placeholders. It can make counting Sig. Figs difficult.

Significant Figures How do you decide if a “ 0” is significant? • 1. All non-zero numbers are Sig. Figs (3. 21 = 3 sigfig) • 2. Zeros located between non-zero digits are Sig. Figs (102 = 3 sigfigs) • 3. Final zeros (those at the end) are Sig. Figs if the # contains a decimal point; otherwise they are not. (1. 000 = 4 sigfig) (1000 = 1 sigfig) • 4. Zeros to left of the first nonzero digit are never Sig. Figs; they are only placeholders (0. 00123 = 3 sigfigs)

Sig. Figs. • If the zeroes were actually measured or if they were the 1 st estimated digit, they are sig figs. If they are just placeholders, they are not.

Sig. Figs. How to figure out the # of sig figs in a number: • 1) If there is no decimal point, start at the RIGHT and count, beginning with the first non-zero digit. • Examples – 450 has 2 sig figs – 10300 has 3 sig figs – 60056 has 5 sig figs

• 2) If there is a decimal point, start at the LEFT and count, beginning with the first non-zero digit. • Examples – 340. has 3 sig figs – 30400. has 5 sig figs – 0. 34955 has 5 sig figs – 0. 00040 has 2 sig figs

Sig. Figs. • Counted numbers and conversion factors are considered to be infinitely significant. – 8 atoms – 5 electron pairs – 12 inches in a foot – 1000 m in a km • There are no Sig. Figs in any of these numbers because they are not measurements!

Sig. Figs. • Chemistry involves a lot of math • When you are performing calculations, you have to obey special rules for how many Sig. Figs your answers are allowed to have • You also have to know when and how to round off your answers in order to comply with the Sig. Fig rules

Sig. Figs. • Calculators are time-savers and we will use them in this class. • Remember, calculators don’t know how to round your answer to the correct number of Sig. Figs.

Sig. Figs. • Calculators give answers with as many digits as the display can show. • This may make you think that your answer is more precise than it actually is. • Making sure that your final answer has the correct number of Sig. Figs often requires rounding the results of a calculation

Sig. Figs. • Use the following rules for rounding: 1. If the digit after the last Sig. Fig is <5, round down • 10. 13 becomes 10. 2 (assuming 3 SFs allowed) 2. If the digit after the last sigfig is >5, round up • 13. 48 becomes 13. 5 (assuming 3 SFs allowed) 3. If the digit after the last Sig. Fig = 5, go to the next number to make your decision • 28. 52 becomes 28. 5 (assuming 3 SFs) • 13. 58 becomes 13. 6 (assuming 3 SFs)

Sig. Figs. • Rules for rounding in a series of calculations If you need to report an intermediate answer, it should be rounded using the sigfig rules. However, continuing calculations involving that number should be done with the unrounded value. Leave rounding until the end.

Sig. Figs. • Rules for calculating with Sig. Figs • The # of Sig. Figs in a calculated answer depends on the # of Sig. Figs in each measurement used in the calculation.

Sig. Figs. • Your calculated answer cannot be more significant than the least significant quantity used in the calculation – Since the # of Sig. Figs tells you how precise your data is, if you use too many figures you are exaggerating your precision. – 2. 0 + 2. 0 DOES NOT equal 4. 00000

Sig. Figs. • The # of Sig. Figs your answer can have depends on the kind of operation you are doing – Addition/Subtraction – Multiplication/Division – Mixed Math

Sig. Figs. • If you are adding or subtracting, the answer has the same # of decimal places as that of the least given. – If next # is 0 -4, round down. If it is 5 -9, round up

Sig. Figs. • 1) 127. 89 + 0. 002 = • 2) 17. 95+13. 42+50= • 3) 8. 5+2. 7+1. 97= • 4) 84. 577 -3= • 5) 76 -2. 53= • 6) 10 -7. 9=

Sig. Figs. • If you are multiplying or dividing, the answer has the same # of sig figs as that of the least given. – If next # is 0 -4, round down. If it is 5 -9, round up

Sig. Figs. Quick Review of Sci. Not Using Calculators 1. Enter the coefficient 2. Hit “EE” or “EXP” • You may have to hit “ 2 nd” first if your calculator does not have any of these as a primary key • NEVER enter “x” then “ 10” manually!! 3. Enter the exponent • To make it negative, hit the (-) or +/- button first 4. Evaluate, add, subtract, multiply, divide

Other Math Skills for Chem • Cross-multiplying • Rearranging equations • Multiplying fractions • Unit conversions

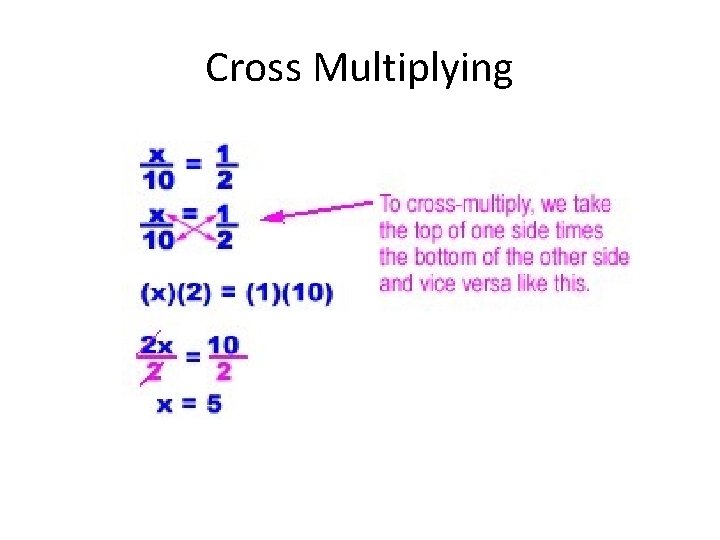
Cross Multiplying

Rearranging Equations Mathematical formulas describe relationships between variables– e. g. , the mass, volume, and density of a substance is described by the formula “D=M/V”. • When doing calculations in chem, you will be given all but one variable and you must rearrange the equation to solve for that variable. – There are 2 simple rules for isolating variables

Rearranging Equations Rule #1: you can +/-/x/÷ by anything, as long as you do the same thing to both sides of the equals sign

Rearranging Equations • Rule #2: to move or cancel a quantity or variable on one side of the equation, perform the "opposite" operation with it on both sides of the equation. • Example – Given the equation s – 6 = p, solve for “s” – isolate “s”, add 6 to both sides (s-6+6 = p+6). – Simplify ( -6 + 6 ) = 0 and end up with s = p+6.

Multiplying Fractions

Unit Conversions • If the same unit is on the diagonal in a conversion string, it will cross-cancel. The remaining unit is the unit of the final answer. • 5. 00 moles C x 12. 01 g = 60. 05 g of carbon 1. 00 mole C • 10. 0 g H 2 x 1 mol H 2 x 22. 4 L H 2 = 110. 89 L H 2 2. 02 g H 2 1 mol H 2 • Every answer must have a unit and a substance or it will be marked wrong!

Unit Conversions • Each equivalency ratio in the conversion string is a step that gets you from one unit to the next is called a conversion factor. • Here are some conversion factors you will be using often in chemistry – 1 mole = 6. 02 x 1023 particles – 1 mole = 22. 4 liters – 1 liter = 1000 m. L – 1 gram = 1000 mg – 1 kg = 1000 g