Chemical Thermodynamics REVERSIBLE PROCESSES Prof Dr Samih A

Chemical Thermodynamics REVERSIBLE PROCESSES Prof. Dr. Samih A. Halawy

Reversible Processes n A thermodynamically reversible process is one which is carried out so very slowly that at every stage of it, the system is in temperature and pressure, equilibrium with its surrounding. In such processes, the driving and opposing forces differ only infinitesimally and the process can be reversed completely by increasing the opposing force by an infinitesimal amount. n

Reversible Processes In a reversible process the system changes in such a way that the system and surroundings can be put back in their original states by exactly reversing the process. Changes are infinitesimally small in a reversible process.

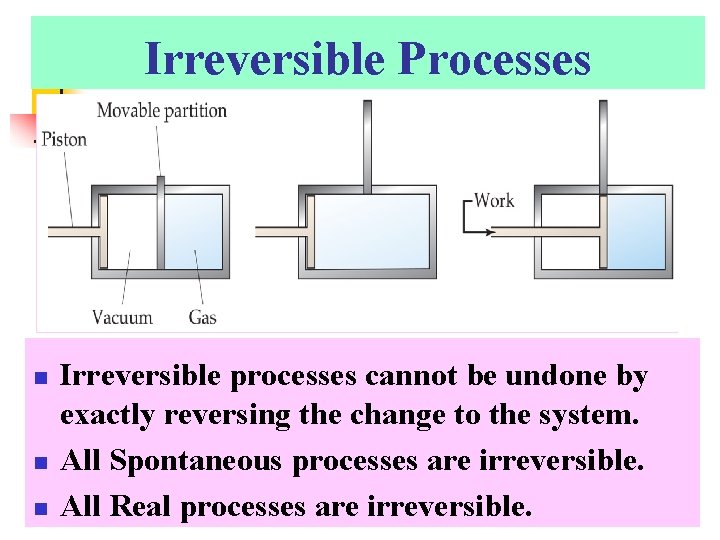
Irreversible Processes n n n Irreversible processes cannot be undone by exactly reversing the change to the system. All Spontaneous processes are irreversible. All Real processes are irreversible.

To understand this concept of reversibility, imagine a cylinder containing some water in equilibrium with its vapour and fitted with a weightless, frictionless piston. Let this cylinder be placed in a constant temperature bath. The driving force on the piston is the external pressure while the opposing force is the vapour pressure of water and as long as these are equal, the system is in perfect equilibrium. Now increase the external pressure by an infinitesimal amount. This will cause the vapour to condense but this condensation will take place so very slowly that the heat given off by this condensation is taken up by the bath and there is no change in the temperature and pressure and at all stage of the condensation of water vapour a state of equilibrium is maintained.

n n In case, however, the vapour pressure is reduced by an infinitesimal amount below the vapour pressure of water, slow evaporation will start. Thus an infinitesimal change in pressure on either side of the equilibrium pressure causes the process to be reversed. Although complete reversibility is more or less hypothetical and cannot be realized due to dissipation of energy in some form by friction etc. , yet it can be approached and it is determined by the difference between the driving and the opposing forces. Spontaneous processes like the expansion of a gas into a vacuum the flow of heat from a hot body to a colder body in contact with it or in diffusion of one gas into another always proceed in a direction of greater stability and are, therefore, reversible.

REVERSIBILTTY AND MAXIMUM WORK n n n Consider a perfect gas enclosed in a cylinder provided with a weightless and frictionless piston. Let its pressure be (p) which in a state of equilibrium is equal to the external pressure on the piston. Let the external pressure be reduced by an infinitesimal amount p and let the small increase in volume be (d. V) which causes the piston to move up. Work done by the gas = (p-dp). d. V (1) It is evident that smaller the value of (dp), the greater is the work done or that the work that can be obtained from a system is the maximum when the external pressure of the gas.

n n Incidentally, the conditions of reversibility of a process are identically the same and it may, therefore, be stated that maximum work can be obtained from a process only when it is carried out reversibly and isothermally. To calculate the maximum work done, when an ideal gas expands isothermally and reversibly from V 1 to V 2, we have to add all the infinitesimally small amount of work represented by equation : - d. W = (p - dp). d. V Neglecting the very small term (dp. d. V) d. W = p. dp (1)

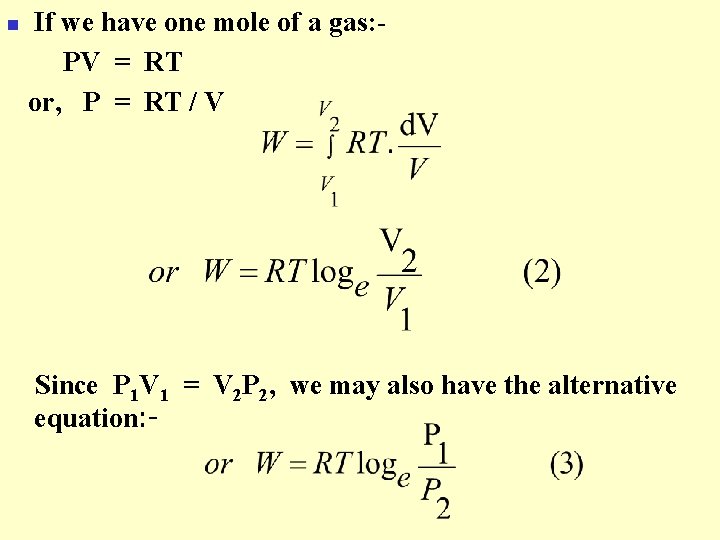
n If we have one mole of a gas: PV = RT or, P = RT / V Since P 1 V 1 = V 2 P 2, we may also have the alternative equation: -

n n n n n Equation (2) and (3) give the maximum work obtainable from an isothermal reversible expansion of one gram mol. of an ideal gas. Example: Calculate the maximum work done by one mole of gas during its expansion from volume 2. 24 L to volume 22. 4 L at 0 C. Answer: (R = 1. 987 cals. /mol. K ) Wmax = n. RT ln V 2/V 1 T = 0 + 273 = 273 K , n =1 mole Wmax = 1 (mole) x 1. 987 (cals. /mol. K ) x 273 K x ln 22. 4/2. 24 Wmax = 1. 987 x 273 x 2. 303 = 1249 cals.