Chemical Reaction on the BornOppenheimer surface and beyond

Chemical Reaction on the Born-Oppenheimer surface and beyond ISSP Osamu Sugino FADFT WORKSHOP 26 th July

Chemical Reaction • On the (ground state) Born-Oppenheimer surface – Thermally activated process: Classical • Beyond: excited state potential surface – Non-adiabatic reaction: Quantum – Dissipation (dephasing): Classical aspect

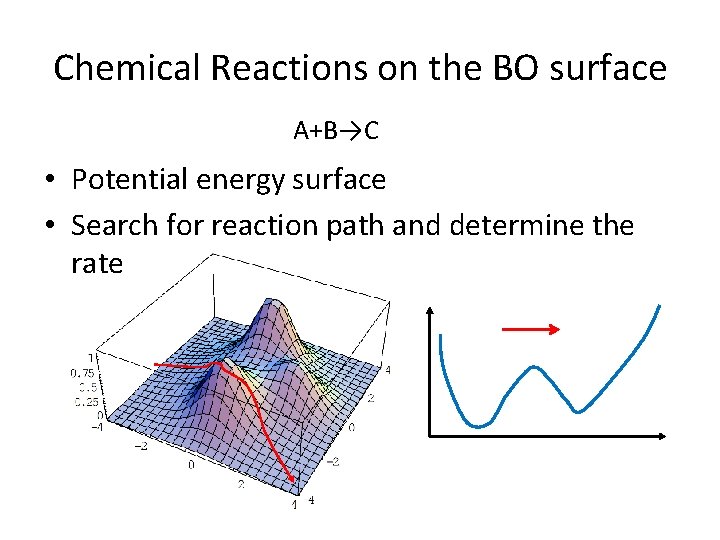
Chemical Reactions on the BO surface A+B→C • Potential energy surface • Search for reaction path and determine the rate

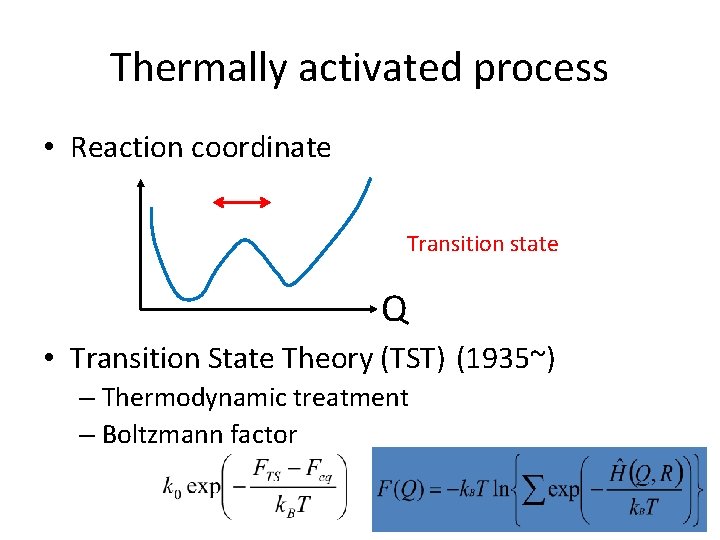
Thermally activated process • Reaction coordinate Transition state Q • Transition State Theory (TST) (1935~) – Thermodynamic treatment – Boltzmann factor

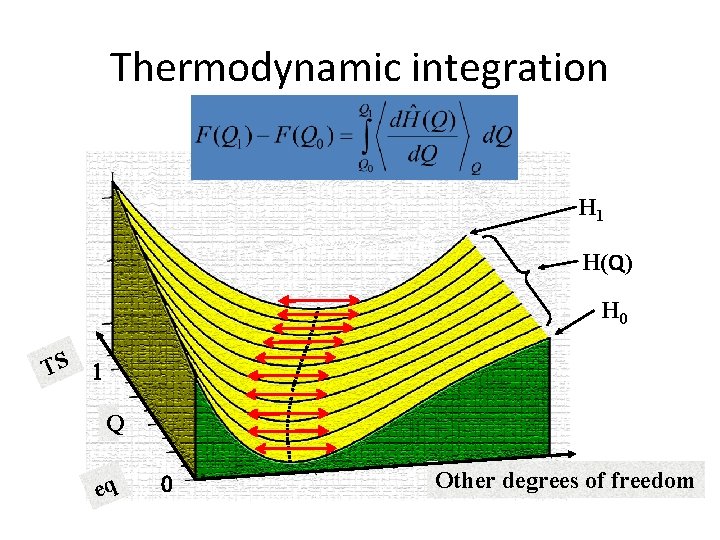
Thermodynamic integration H 1 H(Q) H 0 TS 1 Q eq 0 Other degrees of freedom

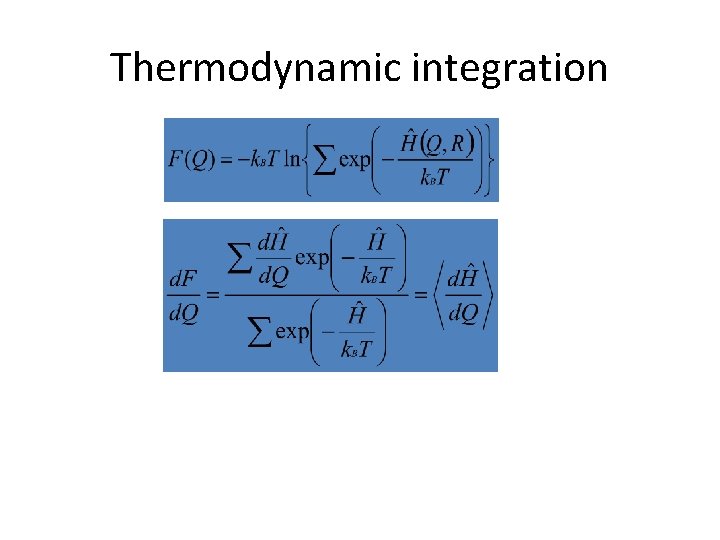
Thermodynamic integration

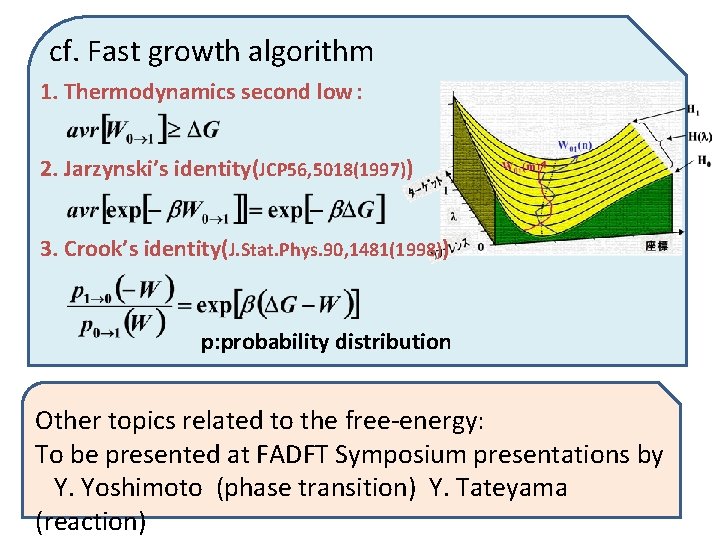
cf. Fast growth algorithm 1. Thermodynamics second low： 2. Jarzynski’s identity(JCP 56, 5018(1997)) 3. Crook’s identity(J. Stat. Phys. 90, 1481(1998)) p: probability distribution Other topics related to the free-energy: To be presented at FADFT Symposium presentations by Y. Yoshimoto (phase transition) Y. Tateyama (reaction)

Free-energy vs. direct simulation • Free-energy approach – TS and Q need to be defined a priori Solvated systems • Water fluctuates • Retarded interaction (dynamical correlation) • Direct simulation – The more important the more complex

An example of the direct simulation Chemical reaction at electrodesolution interface To be presented by M. Otani, FADFT Symposium

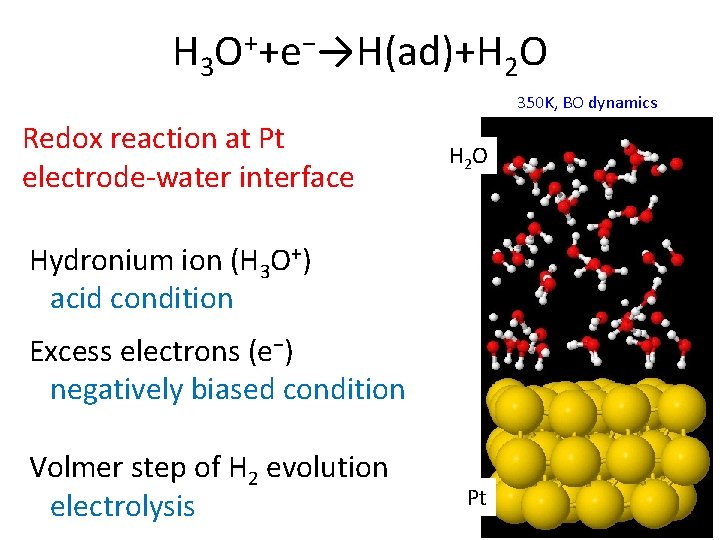
H 3 O++e−→H(ad)+H 2 O 350 K, BO dynamics Redox reaction at Pt electrode-water interface H 2 O Hydronium ion (H 3 O+) acid condition Excess electrons (e−) negatively biased condition Volmer step of H 2 evolution electrolysis Pt

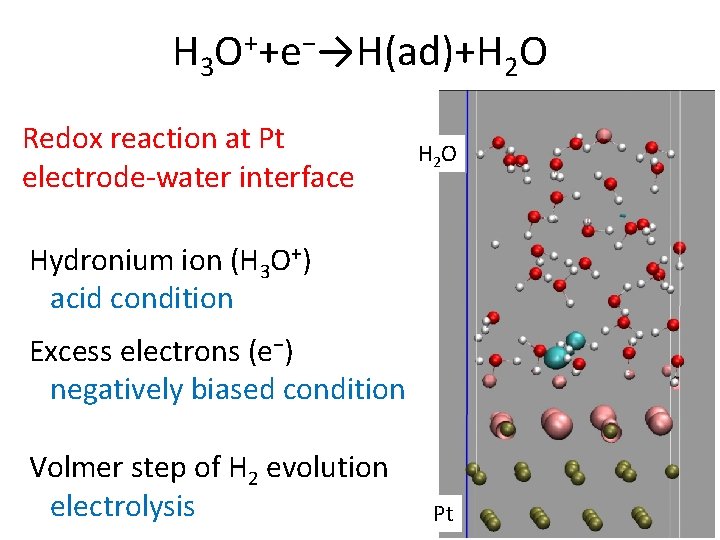
H 3 O++e−→H(ad)+H 2 O Redox reaction at Pt electrode-water interface H 2 O Hydronium ion (H 3 O+) acid condition Excess electrons (e−) negatively biased condition Volmer step of H 2 evolution electrolysis Pt

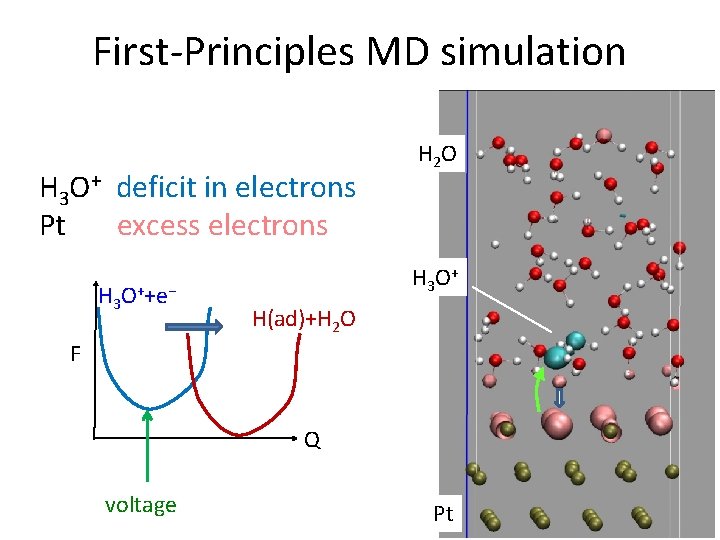
First-Principles MD simulation H 3 O+ deficit in electrons Pt excess electrons H 3 O++e− H 2 O H 3 O + H(ad)+H 2 O F Q voltage Pt

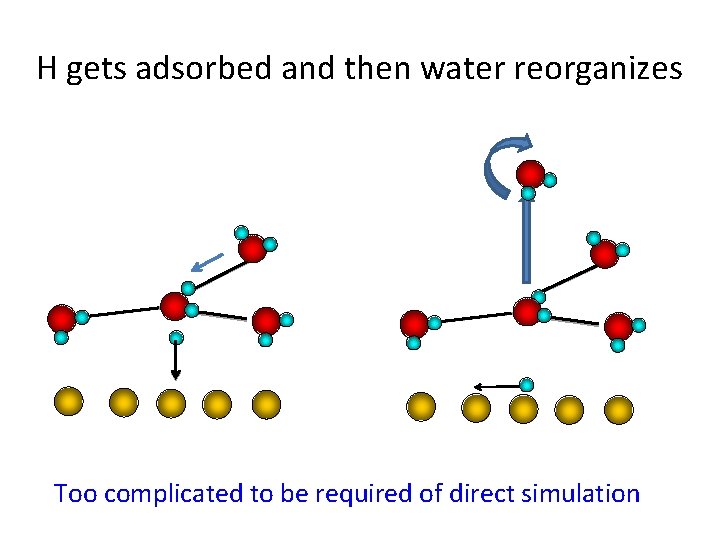
H gets adsorbed and then water reorganizes Too complicated to be required of direct simulation

Chemical reaction beyond BO Non-adiabatic dynamics

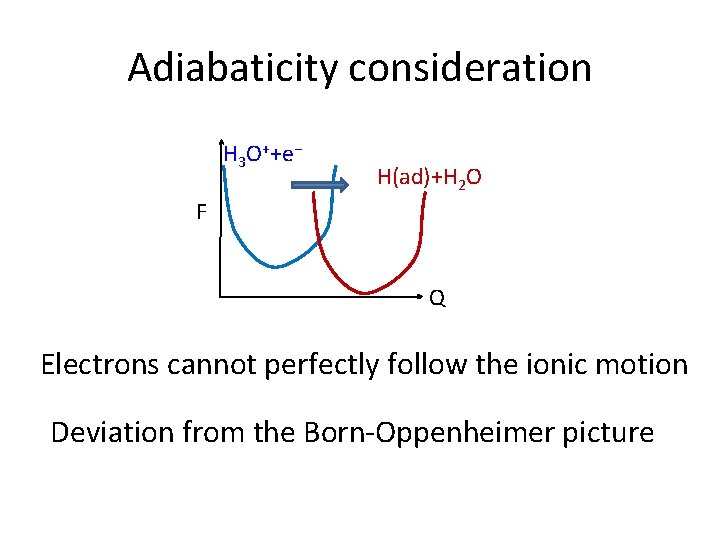
Adiabaticity consideration H 3 O++e− H(ad)+H 2 O F Q Electrons cannot perfectly follow the ionic motion Deviation from the Born-Oppenheimer picture

Non-adiabaticity adiabatic

Wavefunction at t+dt

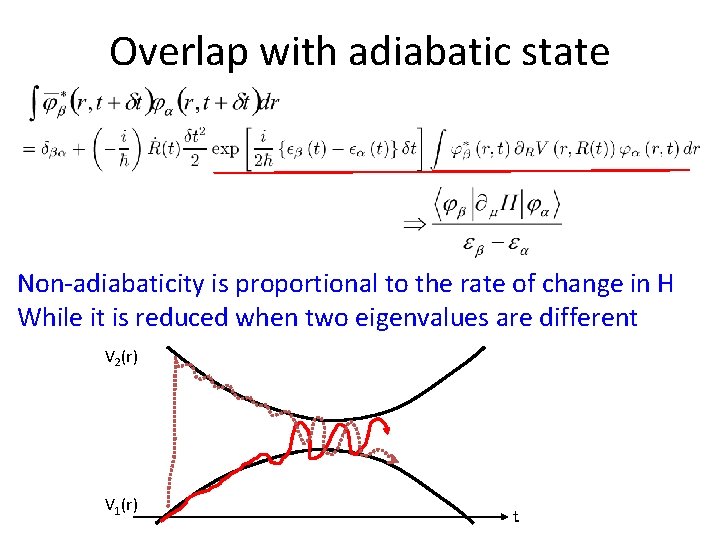
Overlap with adiabatic state Non-adiabaticity is proportional to the rate of change in H While it is reduced when two eigenvalues are different V 2(r) V 1(r) ｔ

Born-Oppenheimer Theory Adiabatic base Density matrix Eq. of motion

A representation of the density matrix Effective nuclear Hamiltonian Potential surfaces e and non-adiabatic couplings are required

Semiclassical approximation using the Wigner representation Nuclear wavepacket

Semiclassical wavepacket dynamics requires first order NACs

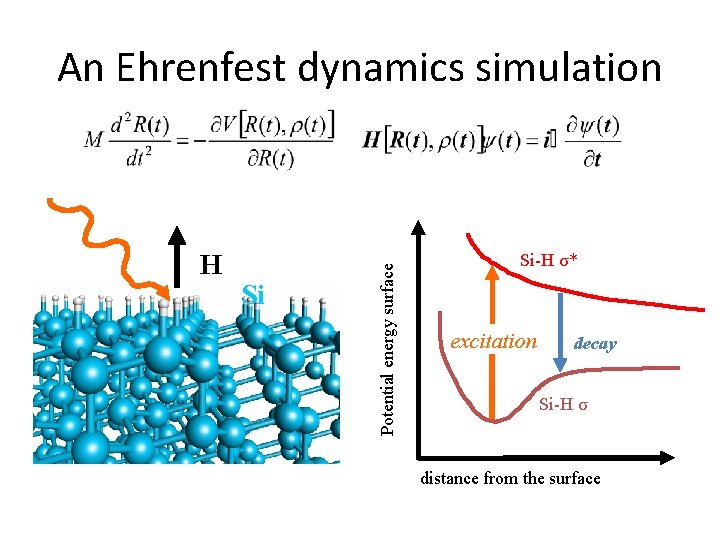
H Si Potential energy surface An Ehrenfest dynamics simulation Si-H σ* excitation decay Si-H σ distance from the surface

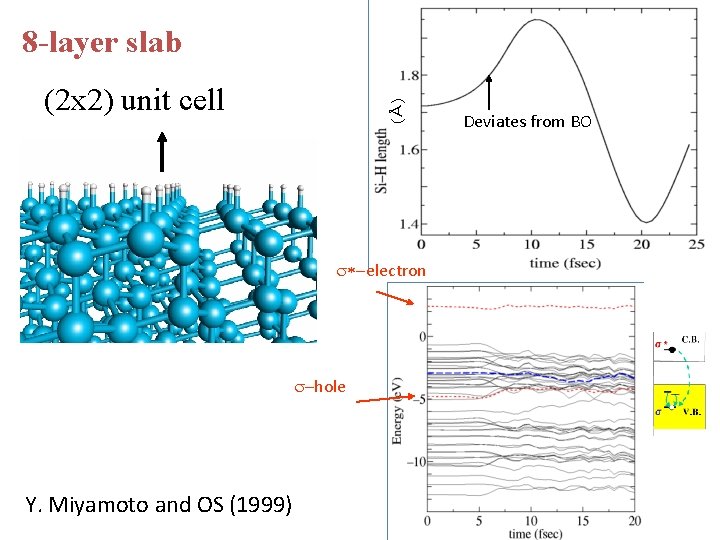
8 -layer slab (Å) (2 x 2) unit cell s*-electron s-hole Y. Miyamoto and OS (1999) Deviates from BO

How to compute NAC TDDFT linear response theory To be presented by C. Hu, FADFT Symposium

How to derive NAC in TDDFT? Apply an artificial perturbation and see the response The sum-over-states (SOS) representation gives Chernyak and Mukamel, JCP 112, 3572 (2000). Hu, Hirai, OS, JCP(2007)

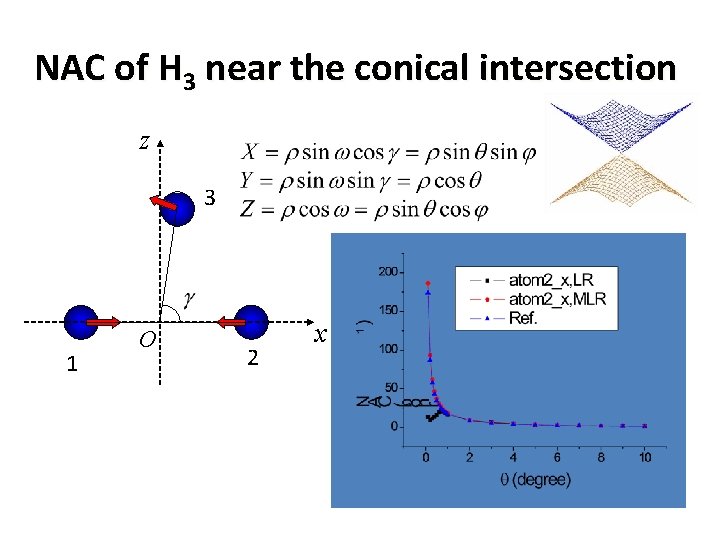
NAC of H 3 near the conical intersection z 3 1 O 2 x

Full Quantum Simulation To be presented by H. Hirai, FADFT Symposium

Summary • Chemical reaction (phase transition, atomic diffusion) – Free-energy approach has become more and more accessible – Direct simulation is very important • Non-adiabatic dynamics – Still challenging but progress has been made for system with few degrees of freedom