Chemical Equilibrium The study of reactions that occur

Chemical Equilibrium The study of reactions that occur in both directions.

So far with reactions…. n Looked at reactions that go to completion n Used stoichiometry for calculation of many quantities n Looked at spontaneity and rates of reactions

Now… n Reactions can be reversible – They reach a state of equilibrium

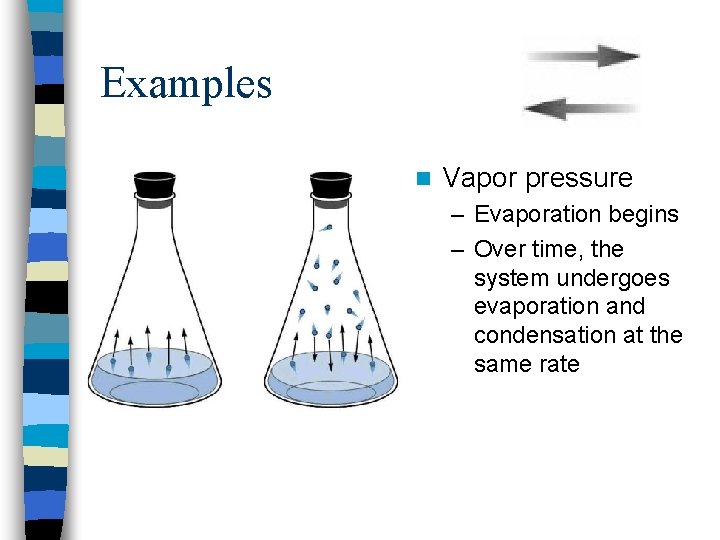
Examples n Vapor pressure – Evaporation begins – Over time, the system undergoes evaporation and condensation at the same rate

Examples n Dissolving and Crystallization – A system could have an equal amount of precipitate (changes states at an equal rate) System of iron (II) dichromate at equilibrium

Examples NO 2 Equilibrium!! N 2 O 4 n NO 2 (g) + NO 2 (g) N 2 O 4 (g) – NO 2 = dark brown, N 2 O 4 = colorless – Ultimately ends up somewhere in between Equlibrium Change in Action

Equilibrium Defined n Concentration of products and reactants remain constant over time – The reaction is reversible (can go both directions) – The rate of forward reaction equals the rate of the reverse reaction – Dynamic!! (looks the same when taking a snapshot, but constantly moving back and forth)

Demo, then Graph of Equilibrium [R] [P] Time

Explaining the Graph [R] What’s happening to the products? n What’s happening to the reactants? n Which one is favored? n Different reactions have different equilibria… n [P] Time

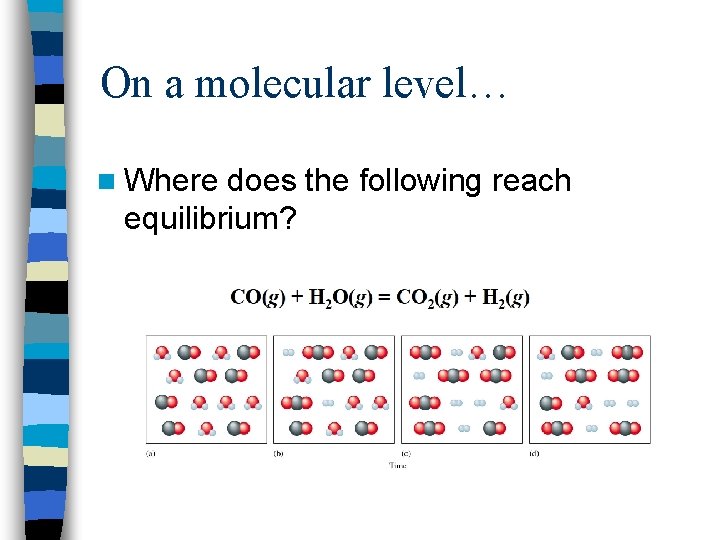
On a molecular level… n Where does the following reach equilibrium?

Equilibrium Expressions n Idea by Guldberg and Waage (1864) – Called the Law of Mass Action – Given a reaction: a. A + b. B c. C + d. D

Equilibrium Expressions n a. A + b. B c. C + d. D [C]c [D]d = [A]a [B]b Equilibrium constant MUST use concentrations of products over reactants coefficients of balanced equation become exponents

Equilibrium Expressions [C]c [D]d = [A]a [B]b n Works only for GASES and IONS – No pure solids or liquids included n Example – C 3 H 8 (g) + O 2 (g) CO 2 (g) + H 2 O (g) [CO 2]3 [H 2 O]4 = [C 3 H 8] [O 2]5

Equilibrium Expressions n What if it has solids or liquids? – Called heterogeneous equilibrium – The concentration of solids and liquids is assumed to always remain constant, so they are not included… – Example: Ca (s) + O 2 (g) Ca. O (s)

Equilibrium Expressions n More examples – H 2 (g) + I 2 (s) 2 HI (g) – Cu. SO 4 5 H 2 O (s) Cu. SO 4 (s) + 5 H 2 O (g) – N 2 (g) + 3 H 2 (g) 2 NH 3 (g)

Values of K n Equilibrium constant, K, is found by: [products] [reactants] – If K = 1…. . • equal ratio of products and reactants – If K > 1 …. • reaction favors products – If K < 1 …. • reaction favors reactants

What changes K? 1. Change the temperature. – Equilibrium is temperature dependent.

What changes K? 2. Change the reaction – Look at the original reaction and see the change that was made to it. • – Whatever you do to the reaction, you do to the power of K Example • 2 NO(g) + O 2 (g) 2 NO 2 (g) 1) Change the coefficients • • • K= 4. 67 x 1013 NO(g) + 1/2 O 2 (g) NO 2 (g) What is the change? K’ = K 1/2 = (4. 67 x 1013)1/2 = 6. 83 x 106

What changes K? 2. Change the reaction – Look at the original reaction and see the change that was made to it. • – Whatever you do to the reaction, you do to the power of K Example • 2 NO(g) + O 2 (g) 2 NO 2 (g) 2) Reverse the reaction • • • K= 4. 67 x 1013 2 NO 2 (g) 2 NO (g) + O 2 (g) What is the change? K’ = 1/K = 1/(4. 67 x 1013) = 2. 14 x 10 -14

Equilibrium Constant n Can also find from reaction mechanism – OVERALL: • N 2 O(g) + 3/2 O 2 (g) 2 NO 2 (g) Kc = ? ? – Steps: • N 2 O(g) + 1/2 O 2 (g) 2 NO (g) • 2 NO(g) + O 2 (g) 2 NO 2 (g) – To find Kc? • Kc = K c 1 x K c 2 Kc 1 = 1. 7 x 10 -13 Kc 2 = 4. 67 x 1013

Equilibrium including Gases n Look at partial pressures instead of molarities – a. A (g) + b. B (g) c. C (g) + d. D (g) (PC)c (PD)d = (PA)a (PB)b

Equilibrium including Gases n If it says Kp, you must use pressures – Given moles and L, must use temperature and PV = n. RT to get pressures of each species n. K or Kc is still molarity

Practice Problems n Write equilibrium expressions for: – a) 2 O 3(g) 3 O 2(g) – b) 2 NO(g) + Cl 2(g) 2 NOCl(g) – c) Ba. SO 4(s) Ba+2(aq) + SO 4 -2(aq)

Practice Problems n Changing K by changing the equation – Original equation: 2 NO (g) + O 2 (g) 2 NO 2 (g) • NO (g) + ½ O 2 (g) NO 2 • 2 NO 2 (g) 2 NO (g) + O 2 (g) Keq = 0. 00103

Equilibrium Calculations

Value of the Equilibrium Constant K tells where the equilibrium lies • How likely (to what extent) the reaction is to occur • Does not give rate (that’s KINETICS) • • Three possibilities 1. K=1 • • Equal ratio of products to reactants Equilibrium lies in the “middle”

Value of the Equilibrium Constant K tells where the equilibrium lies • How likely (to what extent) the reaction is to occur • Does not give rate (that’s KINETICS) • • Three possibilities 2. K >1 • • • Bigger number on top, so… More products Equilibrium favors the PRODUCTS (to the right)

Value of the Equilibrium Constant K tells where the equilibrium lies • How likely (to what extent) the reaction is to occur • Does not give rate (that’s KINETICS) • • Three possibilities 3. K <1 • • • Bigger number on bottom, so… More reactants Equilibrium favors the REACTANTS (to the left)

Reaction Quotient (Q) Where you are at

Reaction Quotient (Q) • Snapshot of reaction at some point • Same calculation as Kc [C]c [D]d = [A]a [B]b • They will give you the K of the reaction • Compare Q and K

Reaction Quotient (Q) • Example: • 2 NO 2 (g) N 2 O 4 (g) Kp = 11 @ 100°C • 0. 200 moles of NO 2 are mixed with 0. 200 moles of N 2 O 4 in a 4. 00 L flask at 100°C. [N 2 O 4] = [NO ]2 = 1. 5 atm 2

Reaction Quotient (Q) Where am I? ? • Kp = 11, Q = 1. 5 • • Compare Q to K to see where you are • 3 situations 1. Q=K • At EQUILIBRIUM!!

Reaction Quotient (Q) Where am I? ? • Kp = 11, Q = 1. 5 • • Compare Q to K to see where you are • 3 situations 2. Q>K • • • Bigger number, so… Favors products Must shift left (towards reactants to get to equilibrium)

Reaction Quotient (Q) Where am I? ? • Kp = 11, Q = 1. 5 • • Compare Q to K to see where you are • 3 situations 3. Q<K • • • Smaller number, so… Favors reactants Must shift right (towards products to get to equilibrium)

IMPORTANT PROBLEM § Calculate concentrations at equilibrium § Use an ICE table

ICE Problems § Steps for doing an ICE problem 1. Write a balanced equation 2. Write your equilibrium expression 3. Calculate Q and see which way it will shift/change to reach equilibrium (usually don’t have to do this if just given reactants initially)

ICE Problems 4. Set up ICE I = initial concentration + C = change in concentration E = equilibrium concentration

ICE Problems 5. Solve for x 6. Find equilibrium concentrations 7. Check by plugging in equilibrium concentrations (it should equal K – or really close)

ICE Example – fairly simple § CO (g) + H 2 O (g) CO 2 (g) + H 2 (g) § Carbon monoxide reacts with steam to produce carbon dioxide and hydrogen. At 700 K the equilibrium constant is 5. 10. Calculate the equilibrium concentrations of all species if 1. 000 mol of each component is mixed in a 1. 000 -L flask.

ICE Example – fairly simple § CO (g) + H 2 O (g) CO 2 (g) + H 2 (g) § K = 5. 10, [] of all is 1. 000 M (NOT at equilibrium) 1. Write a balanced equation. CHECK!

ICE Example – fairly simple § CO (g) + H 2 O (g) CO 2 (g) + H 2 (g) § K = 5. 10, [] of all is 1. 000 M (NOT at equilibrium) 2. Write the equilibrium expression. [CO 2] [H 2] K = [CO] [H O] 2 Also expression for Q…. .

ICE Example – fairly simple § CO (g) + H 2 O (g) CO 2 (g) + H 2 (g) § K = 5. 10, [] of all is 1. 000 M (NOT at equilibrium) 3. Solve for Q and see where you are. [1. 000] Q = [1. 000] = 1. 000 Q is LESS than K, so we are on the reactants side, and we need to shift to products.

ICE Example – fairly simple § CO (g) + H 2 O (g) CO 2 (g) + H 2 (g) 4. Set up ICE!!!!! I +C E CO (g) + H 2 O (g) CO 2 (g) + H 2 (g) 1. 000 -x -x +x +x 1. 000 - x 1. 000+ x 1. 000 + x

ICE Example – fairly simple § CO (g) + H 2 O (g) CO 2 (g) + H 2 (g) § K = 5. 10 5. Plug into expression, solve for x 5. 10 = (1. 000 + x) (1. 000 – x) = (1. 000 + x)2 (1. 000 – x)2 Nice!! Makes this much less ugly

ICE Example – fairly simple § CO (g) + H 2 O (g) CO 2 (g) + H 2 (g) § K = 5. 10 5. Plug into expression, solve for x 5. 10 = (1. 000 + x) (1. 000 – x) x = 0. 387 Just solved for the CHANGE

ICE Example – fairly simple § CO (g) + H 2 O (g) CO 2 (g) + H 2 (g) § x = 0. 387 6. Find equilibrium concentrations. § § [CO] = 1. 000 - x = 0. 613 M [H 2 O] = 1. 000 – x = 0. 613 M [CO 2] = 1. 000 + x = 1. 387 M [H 2] = 1. 000 + x = 1. 387 M

ICE Example – fairly simple § CO (g) + H 2 O (g) CO 2 (g) + H 2 (g) § K = 5. 10 7. Check your equilibrium constant. [1. 387] K = [0. 613] WOO HOO!! = 5. 10

Given Equilibrium Condition § Sulfur trioxide decomposes in a sealed container: 2 SO 3 (g) 2 SO 2 (g) + O 2 (g). Initially, the vessel is charged at 1000 K with SO 3 (g) at a partial pressure of 0. 500 atm. At equilibrium, the partial pressure of SO 3 (g) is 0. 200 atm. Calculate the Kp at 1000 K.

Given Equilibrium Condition § 2 SO 3 (g) 2 SO 2 (g) + O 2 (g) § SO 3 is initially 0. 500 atm, and 0. 200 atm at equilibrium 1. Write a balanced equation. CHECK!

Given Equilibrium Condition § 2 SO 3 (g) 2 SO 2 (g) + O 2 (g) § SO 3 is initially 0. 500 atm, and 0. 200 atm at equilibrium 2. Write the equilibrium expression. K= [SO 2]2 [O 2] [SO 3]2 Don’t need to do Q since starting with just reactants

Given Equilibrium Condition § 2 SO 3 (g) 2 SO 2 (g) + O 2 (g) 4. Set up ICE!!!!! I +C E 2 SO 3 (g) 2 SO 2 (g) + O 2 (g) 0. 500 0 0 -2 x +x 2 x x 0. 200 Stoichiometric relationship!!

Given Equilibrium Condition § 2 SO 3 (g) 2 SO 2 (g) + O 2 (g) 5. Solve for x § § 0. 500 – 2 x = 0. 200 2 x = 0. 300 § x = 0. 150

Given Equilibrium Condition § 2 SO 3 (g) 2 SO 2 (g) + O 2 (g) 6. Find equilibrium pressures. § § § [SO 3] = 0. 200 atm (given) [SO 2] = 2 x = 0. 300 atm [O 2] = x = 0. 150 atm

Given Equilibrium Condition § 2 SO 3 (g) 2 SO 2 (g) + O 2 (g) 7. Solve for your equilibrium constant. K= [0. 300]2 [0. 150] [0. 200]2 = 0. 338

ICE Example – Uglier… § Suppose 3. 000 mol of H 2 and 6. 000 mol of F 2 are mixed in a 3. 000 L flask. Assume Kc = 1. 15 x 102. Find the equilibrium concentration of each species.

ICE Example – Uglier… 1. Write a balanced equation. § H 2 (g) + F 2 (g) 2 HF (g) 2. Write the equilibrium expression. K= [HF]2 [H 2] [F 2]

ICE Example – Uglier… 3. Solve for Q and see where you are. § Don’t need to!! The reaction only has H 2 and F 2, so it hasn’t even started yet. It HAS to start making products.

ICE Example – Uglier… 4. Set up ICE!!!!! (need molarities…. ) I +C E H 2 (g) + F 2 (g) 2 HF 1. 000 2. 000 0 -x -x +2 x 1. 000 - x 2 x Stoichiometric relationship!!

ICE Example – Uglier… § H 2 + F 2 2 HF § K = 1. 15 x 102 5. Plug into expression, solve for x (2 x)2 1. 15 x 102 = (1. 000 – x)(2. 000 – x) Rearrange and solve with the QUADRATIC EQUATION

ICE Example – Uglier… § H 2 + F 2 2 HF § K = 1. 15 x 102 5. Plug into expression, solve for x 111 x 2 – 345 x + 230 = 0 x = 2. 14 OR x = 0. 968 Doesn’t make sense, H 2 was only 1. 000 M to begin with… This one looks good!!! We’ll use it!!!!

ICE Example – Uglier… § H 2 + F 2 2 HF § x = 0. 968 6. Find equilibrium concentrations. § § § [H 2] = 1. 000 – 0. 968 = 0. 032 M [F 2] = 2. 000 – 0. 968 = 1. 032 M [HF] = 0 + 2(0. 968) = 1. 94 M

ICE Example – Uglier… § H 2 + F 2 2 HF § K = 1. 15 x 102 7. Check your equilibrium constant. [1. 94]2 K = [0. 032] [1. 032] YES!!!! = 115

ICE Example – A nicer way … § Gaseous NOCl decomposes to form the gases NO and Cl 2. At 35°C, the equilibrium constant is 1. 6 x 10 -5. In an experiment where 1. 0 mol NOCl is placed in a 2. 0 L flask, what the equilibrium concentrations?

ICE Example – A nicer way… 1. Write a balanced equation. § 2 NOCl (g) 2 NO (g) + Cl 2 (g) 2. Write the equilibrium expression. K= [NO]2 [Cl 2] [NOCl]2

ICE Example – A nicer way… 3. Solve for Q and see where you are. § Don’t need to!! The reaction only has H 2 and F 2, so it hasn’t even started yet. It HAS to start making products.

ICE Example – A nicer way… 4. Set up ICE!!!!! (need molarities…. ) I +C E 2 NOCl (g) 2 NO (g) + Cl 2 (g) 0. 50 0 0 - 2 x +x 2 x x 0. 50 – 2 x

ICE Example – A nicer way… § 2 NOCl (g) 2 NO (g) + Cl 2 (g) § K = 1. 6 x 10 -5 5. Plug into expression, solve for x 1. 6 x 10 -5 = (2 x)2 (x) (0. 50 – 2 x)2 Ewwww……

ICE Example – A nicer way… § 2 NOCl (g) 2 NO (g) + Cl 2 (g) § K = 1. 6 x 10 -5 5. Plug into expression, solve for x 1. 6 x 10 -5 = (2 x)2 (x) (0. 50 – 2 x)2 Assume that since K is small, the change in the reactants will be small enough to assume it is ZERO

ICE Example – A nicer way… § 2 NOCl (g) 2 NO (g) + Cl 2 (g) § K = 1. 6 x 10 -5 5. Plug into expression, solve for x 1. 6 x 10 -5 = 4 x 3 (0. 50)2 MUCH nicer…. . x = 1. 0 x 10 -2

ICE Example – A nicer way… § 2 NOCl (g) 2 NO (g) + Cl 2 (g) § K = 1. 6 x 10 -5 5. Plug into expression, solve for x x = 1. 0 x 10 -2 • We should check the approximation using the 5% rule • x should be less than 5% of the initial concentration

ICE Example – A nicer way… § 2 NOCl (g) 2 NO (g) + Cl 2 (g) § x = 1. 0 x 10 -2 = 0. 010 6. Find equilibrium concentrations. § § § [NOCl] = 0. 50 M [NO] = 2 x = 2(0. 010) = 0. 020 M [Cl 2] = x = 0. 010 M

ICE Example – A nicer way… § 2 NOCl (g) 2 NO (g) + Cl 2 (g) § K = 1. 6 x 10 -5 7. Check your equilibrium constant. K= [0. 020]2 [0. 010] [0. 50]2 SUPER!!! = 1. 6 x 10 -5

Solubility & Equilibrium Ksp

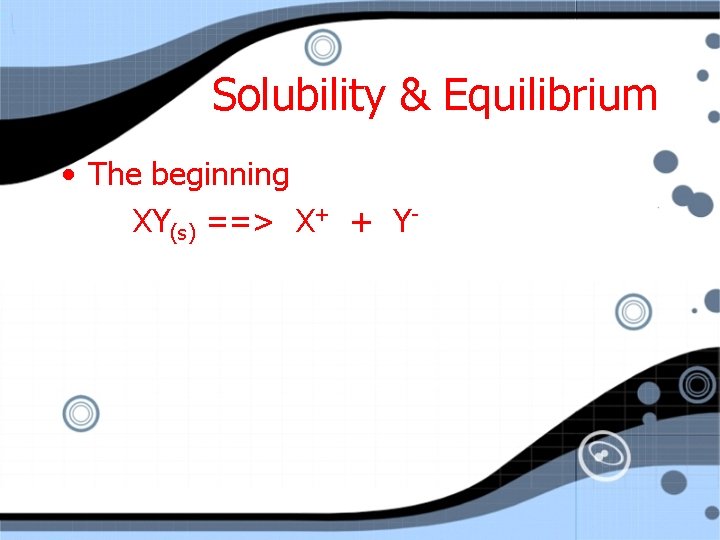
Solubility & Equilibrium • The beginning XY(s) ==> X+ + Y-

Solubility & Equilibrium • The beginning XY(s) ==> X+ + YAs time continues the [ions] begins to increase.

Solubility & Equilibrium Greater the chance that they will collide and reform • XY(s) <== X+ + Y • When it becomes saturated it reaches equilibrium. XY(s) <==> X+ + Y-

Solubility & Equilibrium Constant for Solubility-Ksp = [X+]x [Y-]y Solubility = molar solubility = mol/L • Be careful ~ sometimes given g/L or have to solve for g/L

Solubility & Equilibrium Constant for Solubility-Ksp = [X+]x [Y-]y 1) Just ions, no solids

Solubility & Equilibrium Constant for Solubility-Ksp = [X+]x [Y-]y 2) It doesn’t matter if you have stuff on the bottom.

Solubility & Equilibrium Constant for Solubility-Ksp = [X+]x [Y-]y 3) Not solubility - that’s an equilibrium position(Q) (will more dissolve or not? )

Solubility & Equilibrium Constant for Solubility-Ksp = [X+]x [Y-]y 4) Equilibrium so remember ICE

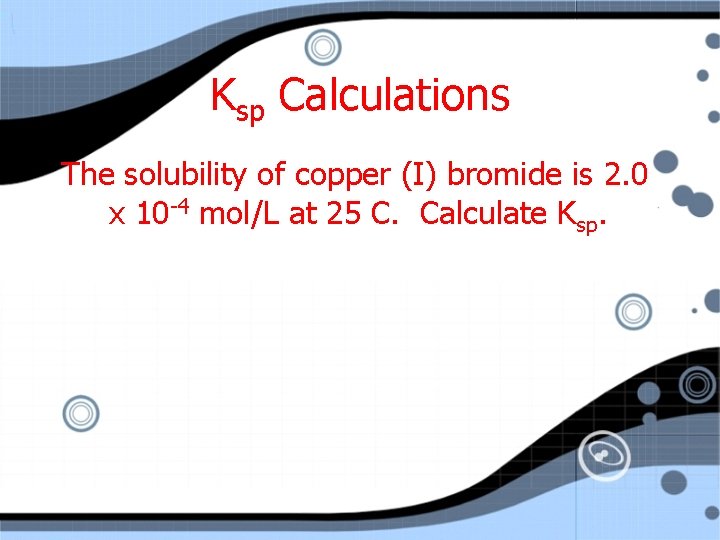
Ksp Calculations The solubility of copper (I) bromide is 2. 0 x 10 -4 mol/L at 25 C. Calculate Ksp.

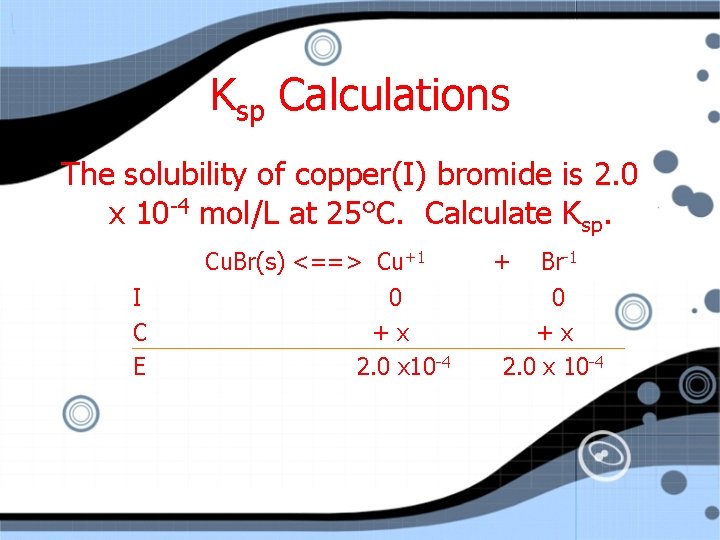
Ksp Calculations The solubility of copper(I) bromide is 2. 0 x 10 -4 mol/L at 25°C. Calculate Ksp. Cu. Br(s) <==> Cu+1 I C E 0 +x 2. 0 x 10 -4 + Br-1 0 +x 2. 0 x 10 -4

Ksp Calculations The solubility of copper(I) bromide is 2. 0 x 10 -4 mol/L at 25°C. Calculate Ksp. Cu. Br(s) <==> Cu+1 + Br-1 Ksp = [2. 0 x 10 -4] = 4. 0 x 10 -8 (no units for K)

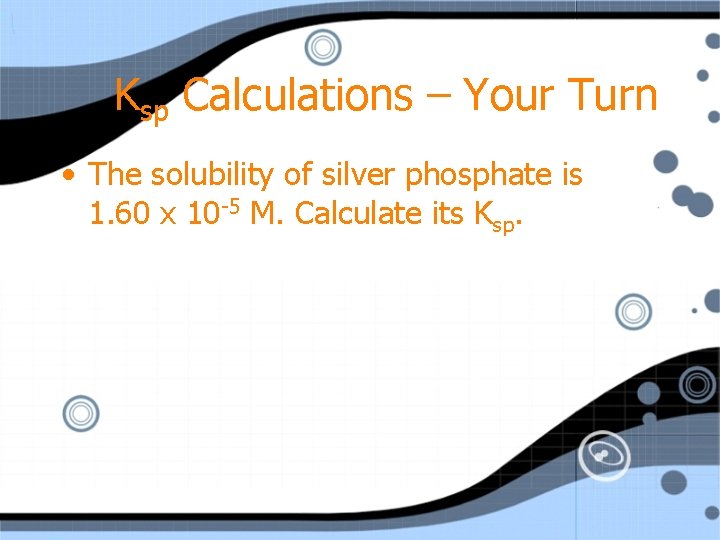
Ksp Calculations – Your Turn • The solubility of silver phosphate is 1. 60 x 10 -5 M. Calculate its Ksp.

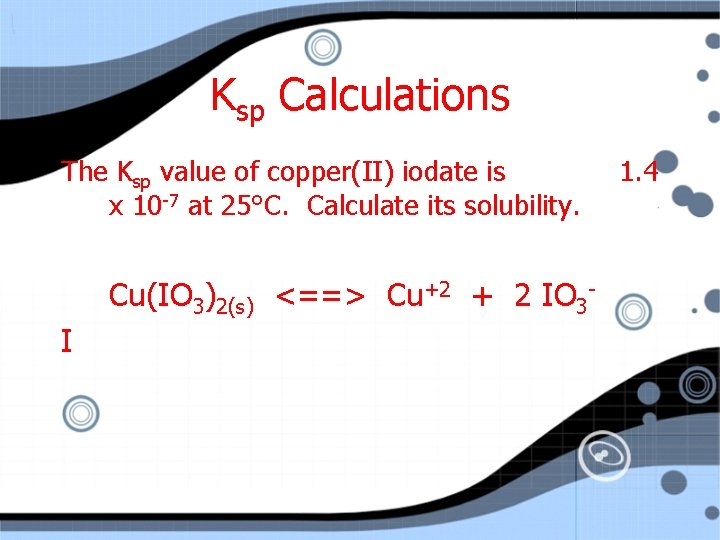
Ksp Calculations The Ksp value of copper(II) iodate is x 10 -7 at 25°C. Calculate its solubility. Cu(IO 3)2(s) <==> Cu+2 + 2 IO 3 I 1. 4

Ksp Calculations The Ksp value of copper(II) iodate is x 10 -7 at 25°C. Calculate its solubility. Cu(IO 3)2(s) <==> Cu+2 + 2 IO 3 I 0 0 C 1. 4

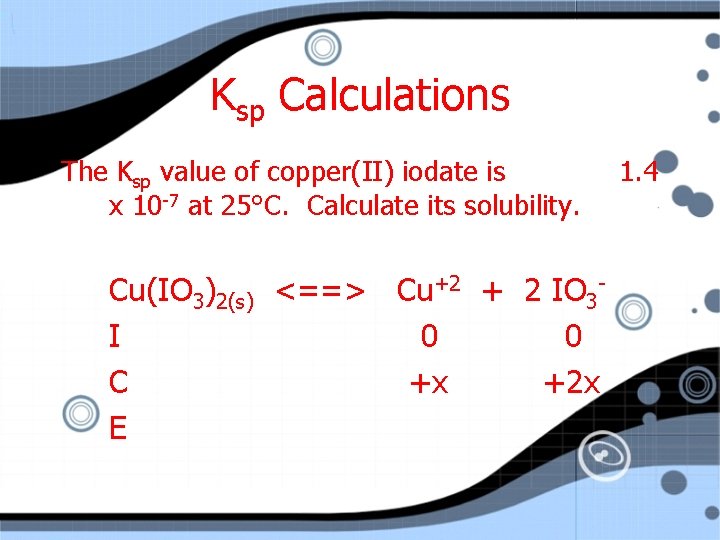
Ksp Calculations The Ksp value of copper(II) iodate is x 10 -7 at 25°C. Calculate its solubility. Cu(IO 3)2(s) <==> Cu+2 + 2 IO 3 I 0 0 C +x +2 x E 1. 4

Ksp Calculations The Ksp value of copper(II) iodate is x 10 -7 at 25°C. Calculate its solubility. Cu(IO 3)2(s) <==> Cu+2 + 2 IO 3 I 0 0 C +x +2 x E +x +2 x 1. 4

Ksp Calculations The Ksp value of copper(II) iodate is x 10 -7 at 25°C. Calculate its solubility. Cu(IO 3)2(s) <==> Cu+2 + 2 IO 3 Ksp = [Cu+2][IO 3 -]2 1. 4

Ksp Calculations The Ksp value of copper(II) iodate is x 10 -7 at 25°C. Calculate its solubility. Cu(IO 3)2(s) <==> Cu+2 + 2 IO 3 Ksp = [Cu+2][IO 3 -]2 Ksp = [x][2 x]2 1. 4

Ksp Calculations The Ksp value of copper(II) iodate is 1. 4 x 10 -7 at 25°C. Calculate its solubility. Cu(IO 3)2(s) <==> Cu+2 + 2 IO 3 Ksp = [Cu+2][IO 3 -]2 Ksp = [x][2 x]2 1. 4 x 10 -7 = [x][2 x]2

Ksp Calculations The Ksp value of copper(II) iodate is 1. 4 x 10 -7 at 25°C. Calculate its solubility. Cu(IO 3)2(s) <==> Cu+2 + 2 IO 3 Ksp = [Cu+2][IO 3 -]2 Ksp = [x][2 x]2 1. 4 x 10 -7 = 4 x 3

Ksp Calculations The Ksp value of copper(II) iodate is 1. 4 x 10 -7 at 25°C. Calculate its solubility. Cu(IO 3)2(s) <==> Cu+2 + 2 IO 3 Ksp = [Cu+2][IO 3 -]2 Ksp = [x][2 x]2 1. 4 x 10 -7 = 4 x 3 x = 3. 3 x 10 -3 mol/L

Ksp Calculations The Ksp value of copper(II) iodate is 1. 4 x 10 -7 at 25°C. Calculate its solubility. Cu(IO 3)2(s) <==> Cu+2 + 2 IO 3[Cu+2] = 3. 3 x 10 -3 mol/L [IO 3 -] =2(3. 3 x 10 -3 mol/L) = 6. 6 x 10 -3 mol/L

Ksp Calculations – Your Turn • The Ksp of mercury (II) sulfide is 1. 6 x 10 -54. Find its molar solubility.

Ksp Calculations What does it all mean? According to Ksp, EVERYTHING is at least very, very slightly soluble. Looking at the Ksp can help you figure out the solubility of compounds compared to each other – with a couple key rules about doing it!

Ksp Calculations What does it all mean? 1) Salts that produce the same # of ions can be compared to see which one is the most/least soluble. Ag. Br vs Ksp values 5. 0 x 10 -13 Ag. I 1. 5 x 10 -16 Appendix A 25 vs Ag. Cl 1. 6 x 10 -10

Ksp Calculations What does it all mean? 2) If the salts break into different # of ions, you can’t just look. Must calculate.

Ksp Calculations 2 example problems: Which is more soluble: copper (II) carbonate or cadmium carbonate? Ksp = 2. 5 x 10 -10 Ksp = 5. 2 x 10 -12

Ksp Calculations 2 example problems: Which is more soluble: tin (II) hydroxide or strontium phosphate? Ksp = 3. 0 x 10 -27 Ksp = 1. 0 x 10 -31