Chemical Equilibrium Big K kinetics rate constant little

Chemical Equilibrium: “Big K” kinetics: rate constant “little k” kinetics “little k” told us how fast a reaction proceeds and is used to indicate a possible mechanism. Eq. tells us to what extent a RXN proceeds to completion. react. prod. @ Eq: rate forward = rate reverse H 2 CO 3(l) H 2 O(l) + CO 2(g) 1

The Equilibrium Constant: K (Temperature Dependent) (mechanism independent) a. A + b. B d. D + e. E Law of Mass Action: Values of Kc are constant for a RXN at a given temperature. Any equilibrium mixture of the above system at that temperature should give the SAME Kc value. 2

We also have Kp which is sometimes used when dealing with gases with the “P” referring to the pressure of the gases. a. A(g) + b. B(g) d. D(g) + e. E(g) Since PV = n. RT (ideal gas law) so pressure is proportional to concentration. moles of GAS 0. 0821 L • atm mol • K temp in K 3

Problem: PCl 3(g) + Cl 2(g) PCl 5(g) In a 5. 00 L vessel (@ 230 o. C) an equilibrium mixture is found to contain: 0. 0185 mol PCl 3, 0. 0158 mol PCl 5 and 0. 0870 mol of Cl 2. Question: determine Kc and Kp Solution: Kc = 49. 08 Question: what does the value of K mean? one mol less gas on product side. 4

Using I. C. E. (Initial, Change, Equilibrium) Problem: Manufacture of Wood Alcohol. A 1. 500 L Vessel was filled with 0. 1500 mol of CO and 0. 300 mol of H 2. @ Eq. @500 K, 0. 1187 mol of CO were present. How many moles of each species were present @ Eq. and what is the value of Kc? CO(g) + 2 H 2(g) CH 3 OH(g) 0. 3000 0 I. 0. 1500 C. -x -2 x +x x 0. 3000 - 2 x 0. 1500 - x E. Since @Eq. there were 0. 1187 mol CO present, 0. 1500 - x = 0. 1187 Therefore x = 0. 0313 We can now solve for each of the other Eq. terms. 5

Problem: Manufacture of Wood Alcohol. A 1. 500 L Vessel was filled with 0. 1500 mol of CO and 0. 300 mol of H 2. @ Eq. @500 K, 0. 1187 mol of CO were present. How many moles of each species were present @ Eq. and what is the value of Kc? I. CO(g) 0. 1500 + 2 H 2(g) 0. 3000 C. -x -2 x CH 3 OH(g) 0 +x x 0. 3000 - 2 x 0. 1500 - x E. Since @Eq. there were 0. 1187 mol CO present, 0. 1500 - x = 0. 1187 Therefore x = 0. 0313 We can now solve for each of the other Eq. terms. H 2: 0. 3000 - 2 x = 0. 2374 moles CH 3 OH: x = 0. 0313 moles CO(g) + 2 H 2(g) Therefore E. 0. 1187 0. 2374 CH 3 OH(g) 0. 0313 6

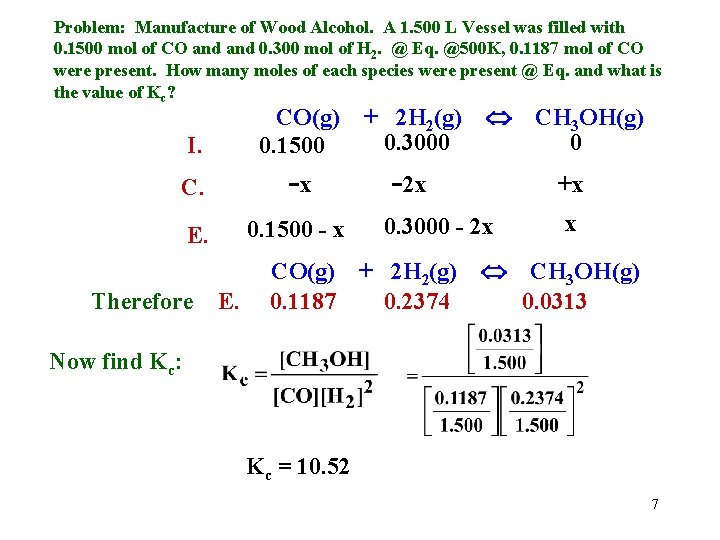
Problem: Manufacture of Wood Alcohol. A 1. 500 L Vessel was filled with 0. 1500 mol of CO and 0. 300 mol of H 2. @ Eq. @500 K, 0. 1187 mol of CO were present. How many moles of each species were present @ Eq. and what is the value of Kc? I. CO(g) 0. 1500 + 2 H 2(g) 0. 3000 C. -x -2 x E. 0. 1500 - x Therefore E. +x 0. 3000 - 2 x CO(g) + 2 H 2(g) 0. 1187 0. 2374 CH 3 OH(g) 0 x CH 3 OH(g) 0. 0313 Now find Kc: Kc = 10. 52 7

More I. C. E. Problem: @ 77 o. C, 2. 00 mol of NOBr (nitrosyl bromide) placed in a 1. 000 L flask dissociates to the extent of 9. 4%. Find Kc. C. 2 NOBr(g) 2. 00 -2 x E. 2. 00 - 2 x I. 2 NO(g) + 0 +2 x 2 x Br 2(g) 0 +x x Now what? Since 9. 4% dissociates, the Change in NOBr, -2 x = 2. 00(0. 094) and. . |x| = 0. 0940 so substituting the x value into the “E. term” gives: 2 NOBr(g) E. 1. 812 2 NO(g) + 0. 188 Br 2(g) 0. 0940 8

More I. C. E. Problem: @ 77 o. C, 2. 00 mol of NOBr (nitrosyl bromide) placed in a 1. 000 L flask dissociates to the extent of 9. 4%. Find Kc. I. C. E. E. 2 NOBr(g) 2. 00 -2 x 2. 00 - 2 x 2 NOBr(g) 1. 812 2 NO(g) + 0 +2 x Br 2(g) 0 +x 2 x 2 NO(g) + x Br 2(g) 0. 188 0. 0940 = 1. 01 x 10 -3 What does the value of Kc tell us? 9

Treatment of Pure Solids and Liquids (as solvents) in K expressions. S(s) + O 2(g) SO 2(g) would expect Kc = [SO 2] [S(s)][O 2] but since M is meaningless for solids, solids are dropped out. and. . . Experimentally Kc is found to be 4. 2 x 1052 @ 25 o. C and independent of S. 10

Ag. Cl(s) Ag+(aq) + Cl-(aq) Ksp = [Ag+(aq)][Cl-(aq)] = 1. 8 x 10 -10 @ 25 o. C This is an EQUILIBRIUM value independent of the amount of solid Ag. Cl left sitting on the bottom of the container. 11

PURE LIQUIDS (SOLVENTS) NH 3(g) + H 2 O(l) NH 4+(aq) + OH-(aq) Note: by convention the water is ignored. HCOOH(aq) + H 2 O(l) HCOO-(aq) + H 3 O+(aq) 12

Ca. CO 3(s) Ca. O(s) + CO 2(g) What is the Kc expression? Kc = [CO 2] What is the Kp expression? Kp = PCO 2 13

Reversing Equations: Reactants become Products and Products become Reactants. What is the relationship between the two K values? 1. 2 H 2(g) + O 2(g) 2 H 2 O(g) 2. 2 H 2 O(g) 2 H 2(g) + O 2(g) Relationship: K 2 = 1/K 1 = K 1 -1 14

Knet for summing RXN’s: If a RXN can be obtained from the sum of RXN’s, KRXN = K 1 K 2 RXN 1: S(s) + O 2 (g) SO 2(g) RXN 2: SO 2(g) + 1/2 O 2(g) SO 3(g) Net RXN: S(s) + 3/2 O 2(g) SO 3(g) KRXN = K 1 K 2 15

The RXN Quotient: Qc Consider a system that may not yet be @ Equilibrium. a. A + b. B d. D + e. E If Qc = Kc ? @ Equilibrium If Qc < Kc ? ratio is too small so RXN If Qc > Kc ? ratio is too large so RXN 16

Example: PCl 5(g) PCl 3(g) + Cl 2(g) @ 250 o. C Kc= 4. 0 x 10 -2 If: [Cl 2] and [PCl 3] = 0. 30 M and [PCl 5] = 3. 0 M, is the system at Equilibrium? If not, which direction will it proceed? Qc = -2 = 3. 0 x 10 Find Qc and compare to Kc to decide. Qc < Kc (not @ Eq. ) Which way must the RXN go to achieve Equilbrium? Remember ratio is prod. /React more products makes the number bigger RXN goes 17

Calculations Using Kc: (1 st case. . Perfect Square) Kc = 55. 17 @ 699 K H 2(g) + I 2(g) 2 HI(g) Experiment: 1. 00 mol of each H 2 and I 2 in a 0. 500 L flask. Find [ ] of products and reactants @ Equilibrium. C. H 2(g) + I 2(g) [ ] 2. 00 -x -x E. 2. 00 -x conc. in mol/L I. 2. 00 - x 2 HI(g) [ ] 0 2 x 2 x = 55. 17 “perfect square” 18

Calculations Using Kc: (1 st case. . Perfect Square--continued) Kc = 55. 17 @ 699 K H 2(g) + I 2(g) 2 HI(g) E. H 2(g) + I 2(g) [ ] 2. 00 -x 2. 00 - x 2 HI(g) [ ] 2 x = 55. 17 “perfect square” 7. 428(2. 00 - x) = 2 x 1. 58 = x 19

Calculations Using Kc: (1 st case. . Perfect Square) @ 699 K H 2(g) + I 2(g) 2 HI(g) E. Kc = 55. 17 H 2(g) + I 2(g) [ ] 2. 00 -x 2. 00 - x 2 HI(g) [ ] 2 x 7. 428(2. 00 - x) = 2 x 1. 58 = x [H 2] = 2. 00 - 1. 58 = 0. 42 M [I 2] = 0. 42 M [HI] = 2(1. 58) = 3. 16 M 20

Kc Problems with Quadratic Equation ax 2 + bx +c = 0 If equilibrium expression is not a perfect square must use quadratic equation. 21

Problem: H 2(g) + I 2(g) 2 HI(g) @ 458 o. C Kc = 49. 7 Experiment: 1. 00 mol H 2, 2. 00 mol I 2 in a 1. 00 L flask. Find: conc. of the equilibrium mixture. I. C. E. H 2(g) + [ ] 1. 00 -x 1. 00 - x I 2(g) 2 HI(g) [ ] 2. 00 0 -x 2 x 2. 00 - x 2 x 0. 920 x 2 - 3. 00 x + 2. 00 = 0 22

Problem: H 2(g) + I 2(g) 2 HI(g) @ 458 o. C Kc = 49. 7 Experiment: 1. 00 mol H 2, 2. 00 mol I 2 in a 1. 00 L flask. Find: conc. of the equilibrium mixture. I. C. E. H 2(g) + [ ] 1. 00 -x 1. 00 - x I 2(g) 2 HI(g) [ ] 2. 00 0 2 x -x 2. 00 - x 2 x 0. 920 x 2 - 3. 00 x + 2. 00 = 0 2 solutions for x: 1. 63 0. 70 x = 2. 33 or 0. 93 will give positive solution for Eq. Conc. 23