Chem E 260 Entropy Generation Fundamental Property Relationships










- Slides: 12

Chem. E 260 Entropy Generation Fundamental Property Relationships Dr. William Baratuci Senior Lecturer Chemical Engineering Department University of Washington TCD 7: C & D CB 6: 2, 7 & 9 May 6, 2005

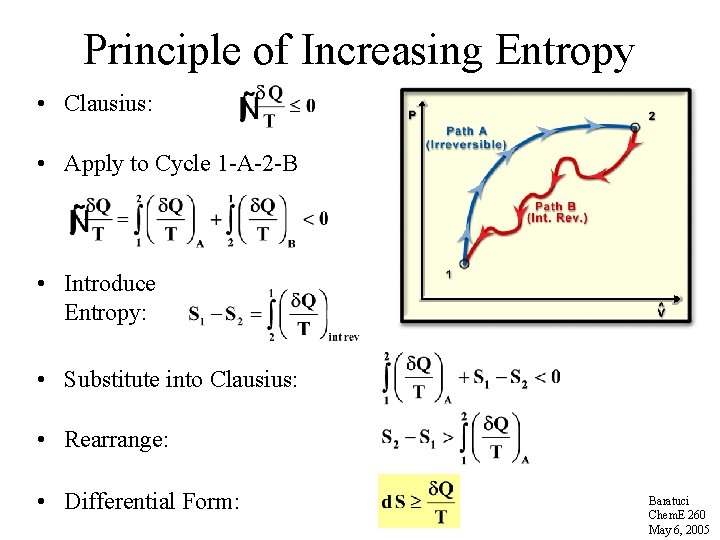
Principle of Increasing Entropy • Clausius: • Apply to Cycle 1 -A-2 -B • Introduce Entropy: • Substitute into Clausius: • Rearrange: • Differential Form: Baratuci Chem. E 260 May 6, 2005

Entropy Generation • Newest Statement of the 2 nd Law : • Make Clausius into an equality: • Entropy Generation, Sgen – Internally reversible processes: – Irreversible processes: – Impossible processes: Baratuci Chem. E 260 May 6, 2005

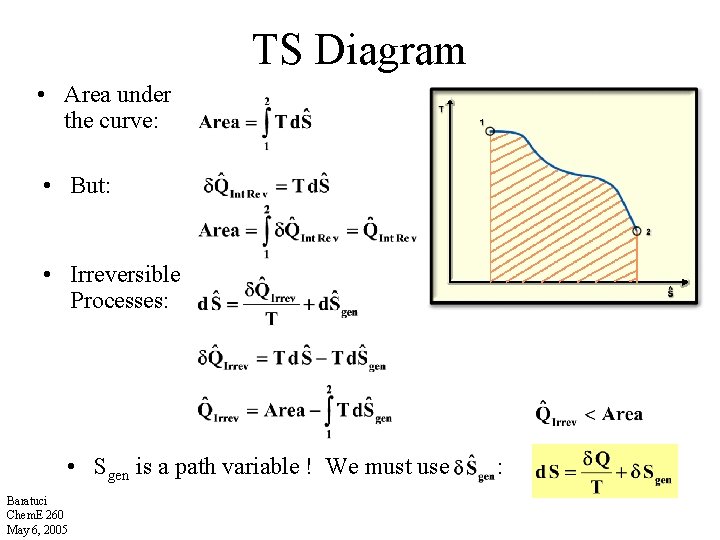
TS Diagram • Area under the curve: • But: • Irreversible Processes: • Sgen is a path variable ! We must use Baratuci Chem. E 260 May 6, 2005 :

Isolated Systems • Entropy Statement of the 2 nd Law: • Isolated Systems, Q = 0, therefore: • The universe is an isolated system: The Principle of Increasing Entropy (a consequence of the 2 nd Law) • Divide the universe into two regions – The system and the surroundings: Baratuci Chem. E 260 May 6, 2005

The Gibbs Equations • Definition of entropy: • 1 st Law, closed system, Wb only: • Boundary work for an internally reversible process: • 1 st Gibbs Equation: • Definition of enthalpy: • Substitute in the 1 st Gibbs Eqn: • 2 nd Gibbs Eqn: Baratuci Chem. E 260 May 6, 2005

Incompressible Liquids • Assumptions: • Gibbs Equations: • Enthalpy, internal energy and heat capacity: • Result: Baratuci Chem. E 260 May 6, 2005

Ideal Gases • Gibbs Equations: • Ideal Gas Heat Capacities and EOS: • Integration yields: Baratuci Chem. E 260 May 6, 2005

Using the Shomate Equation • This method is accurate for ideal gases, but it is tedious. Baratuci Chem. E 260 May 6, 2005

Ideal Gas Entropy Function • Definition: • Relationship with Shomate Eqn : • 1 st Gibbs Eqns for ideal gases : • Substitute the Ideal Gas Entropy Function : Baratuci Chem. E 260 May 6, 2005 Where Tref is the reference temperature at which S = 0.

Ideal Gas Entropy Function • Definition: • Relationship with Shomate Eqn : • 2 nd Gibbs Eqns for ideal gases : • Substitute the Ideal Gas Entropy Function : Baratuci Chem. E 260 May 6, 2005 Where Tref is the reference temperature at which S = 0.

Next Class … • Polytopic Processes: P V = C – More to this type of process than meets the eye – Determination of Boundary Work – PV Diagrams Revisited ! • Isentropic Processes – A special case of the polytropic process – The Relative Property Method of analysis Baratuci Chem. E 260 May 6, 2005