Chem 59 651 Bonding in Molecules Covalent Bonding

Chem 59 -651 Bonding in Molecules Covalent Bonding The term covalent implies sharing of electrons between atoms. Valence electrons and valence shell orbitals - Only valence electrons are used for bonding: ns, np, nd - “Core” electrons are held too tightly (too low in energy) - Filled nd orbitals are considered core electrons Valence state electron configurations and Promotion Energies - The promotion energy is the energy required to promote electrons from the ground state to a “valence state”, which is one type of excited state configuration that is used for bonding. C* E. g. C 2 s 2 2 p 2 ground state 2 s 1 2 p 3 valence state

Chem 59 -651 Localized Bonding Models Localized implies that electrons are confined to a particular bond or atom. The Lewis approach to bonding Pairs of electrons are localized in bonds or as non-bonding “lone pairs” on atoms. Each bond is formed by a pair of electrons shared by two atoms. G. N. Lewis Octet rule: most main group atoms will tend to end up with an ns 2 np 6 electron configuration. ns np This is mostly true for the molecules of organic chemistry not necessarily for inorganic compounds.

Chem 59 -651 Rules for drawing Lewis diagrams a. Pick the central atom. - Atoms that are present only once in the formula, especially heavy elements and metals, tend to be at the center of the structure. - Oxygen is often terminal and hydrogen almost always is. - Often the formula is written with the central atom first. (Sometimes there may be more than one central atom. ) b. Write out the valence shell electron configurations for the neutral central atom and the "terminal" atoms in their ground states. c. If there is a negative charge distribute it among the terminal atoms in the first instance. Bear in mind that all the terminal atoms must make at least one covalent bond with the central atom, so do not create any noble gas configurations on them. Positive charge is best initially assigned by removing electrons from the central atom. d. The total number of unpaired electrons on the terminal atoms will have to match the number of unpaired electrons on the central atom to account for the bonds and leave no unpaired electrons. If this is not the case, once the first three steps have been carried out, there are two strategies available: e. Move electrons between the central atom and the terminal atoms as necessary. Make sure you keep track of the formal charges because you must be specific about their location. Enclosing a Lewis structure in brackets with the charge outside is not acceptable. f. If and only if the central atom comes from the second period or below (Na onwards, n=3 and up), electrons can be placed into the nd subshell. (Whether the d orbitals play a significant role in bonding in main group compounds is debatable, but they do help to predict correct structure without invoking canonical structures with unreasonable charge separations. )

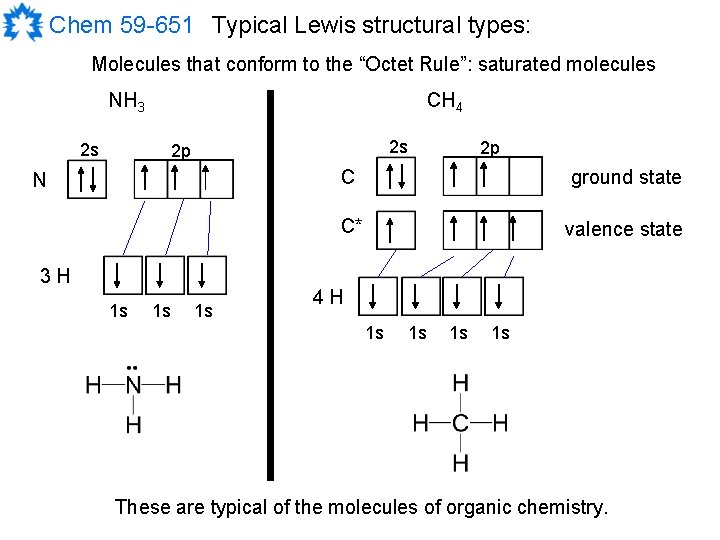
Chem 59 -651 Typical Lewis structural types: Molecules that conform to the “Octet Rule”: saturated molecules NH 3 CH 4 2 s 2 s 2 p N 3 H 1 s 1 s 1 s 2 p C ground state C* valence state 4 H 1 s 1 s These are typical of the molecules of organic chemistry.

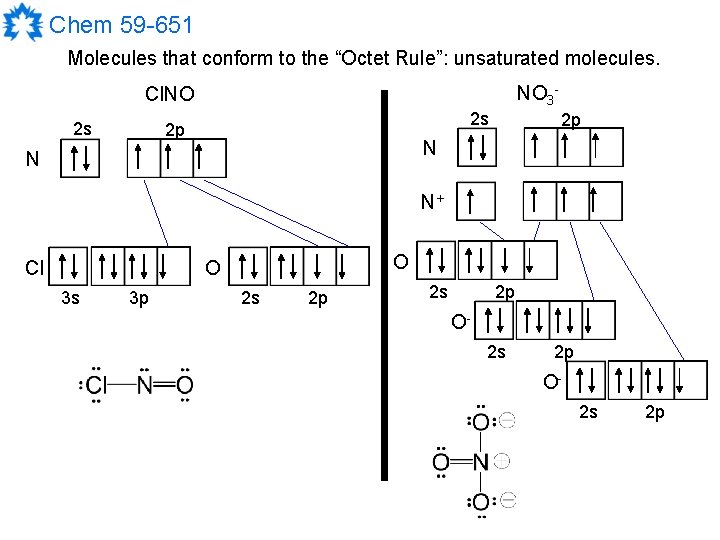
Chem 59 -651 Molecules that conform to the “Octet Rule”: unsaturated molecules. NO 3 - Cl. NO 2 s 2 s 2 p 2 p N N N+ Cl O O 3 s 3 p 2 s 2 p O 2 s 2 p

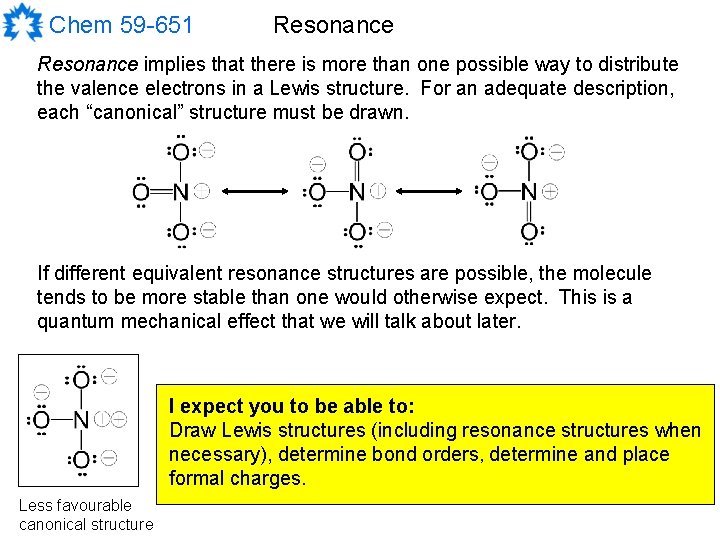
Chem 59 -651 Resonance implies that there is more than one possible way to distribute the valence electrons in a Lewis structure. For an adequate description, each “canonical” structure must be drawn. If different equivalent resonance structures are possible, the molecule tends to be more stable than one would otherwise expect. This is a quantum mechanical effect that we will talk about later. I expect you to be able to: Draw Lewis structures (including resonance structures when necessary), determine bond orders, determine and place formal charges. Less favourable canonical structure

Chem 59 -651 Molecules that don’t conform to the “Octet Rule”: Electron-deficient molecules BH 3 2 s Expanded valence shell molecules Cl. F 3 3 s 2 p 3 p Cl 3 d B Cl* B* F 2 s 3 H 1 s 1 s 1 s 2 p F 2 s “Lewis acids” 2 p “Hypervalent molecules”

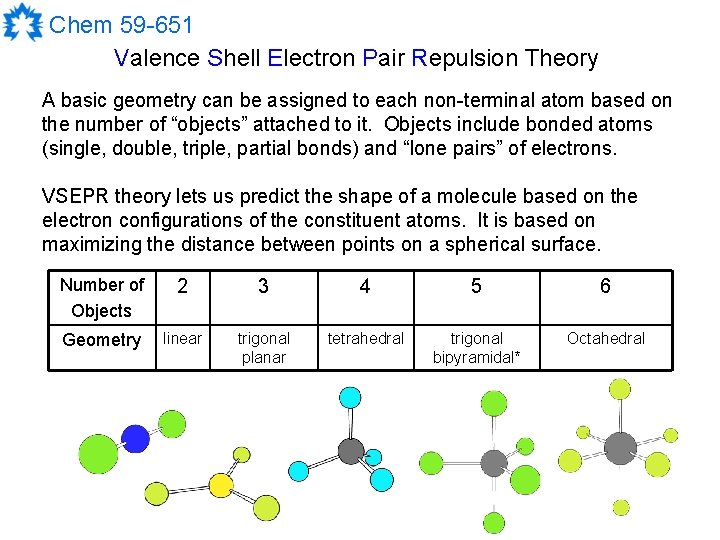
Chem 59 -651 Valence Shell Electron Pair Repulsion Theory A basic geometry can be assigned to each non-terminal atom based on the number of “objects” attached to it. Objects include bonded atoms (single, double, triple, partial bonds) and “lone pairs” of electrons. VSEPR theory lets us predict the shape of a molecule based on the electron configurations of the constituent atoms. It is based on maximizing the distance between points on a spherical surface. Number of Objects 2 3 4 5 6 Geometry linear trigonal planar tetrahedral trigonal bipyramidal* Octahedral

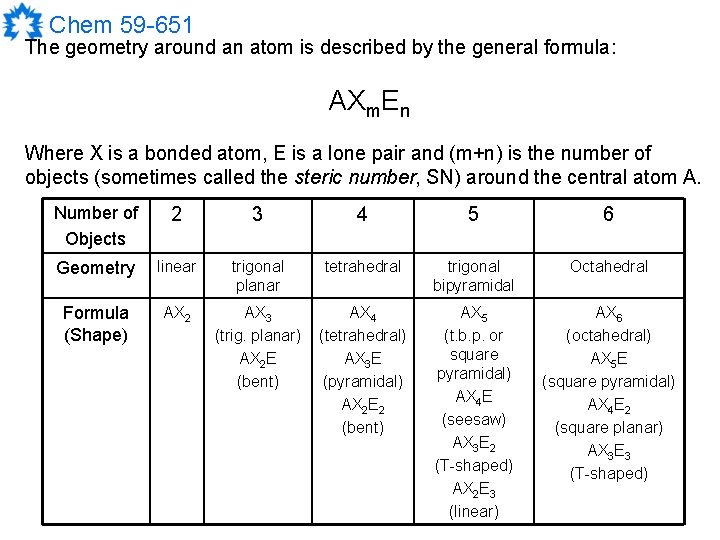
Chem 59 -651 The geometry around an atom is described by the general formula: AXm. En Where X is a bonded atom, E is a lone pair and (m+n) is the number of objects (sometimes called the steric number, SN) around the central atom A. Number of Objects 2 3 4 5 6 Geometry linear trigonal planar tetrahedral trigonal bipyramidal Octahedral Formula (Shape) AX 2 AX 3 (trig. planar) AX 2 E (bent) AX 4 (tetrahedral) AX 3 E (pyramidal) AX 2 E 2 (bent) AX 5 (t. b. p. or square pyramidal) AX 4 E (seesaw) AX 3 E 2 (T-shaped) AX 2 E 3 (linear) AX 6 (octahedral) AX 5 E (square pyramidal) AX 4 E 2 (square planar) AX 3 E 3 (T-shaped)

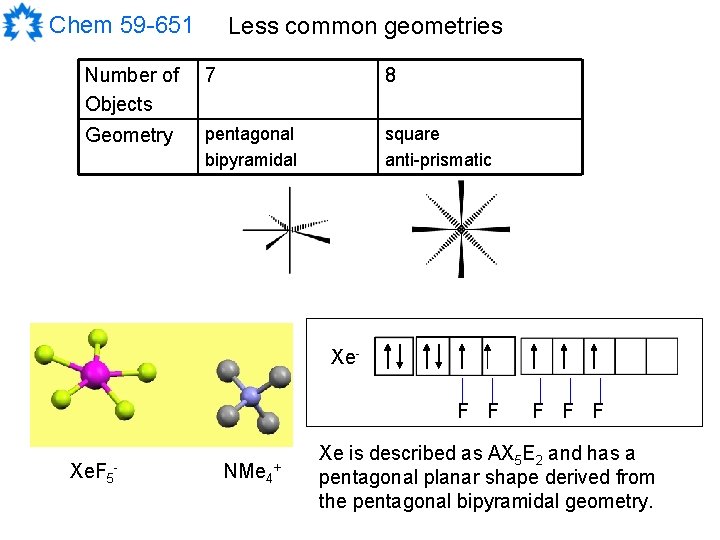
Chem 59 -651 Less common geometries Number of Objects 7 8 Geometry pentagonal bipyramidal square anti-prismatic Xe. F F Xe. F 5 - NMe 4 + F F F Xe is described as AX 5 E 2 and has a pentagonal planar shape derived from the pentagonal bipyramidal geometry.

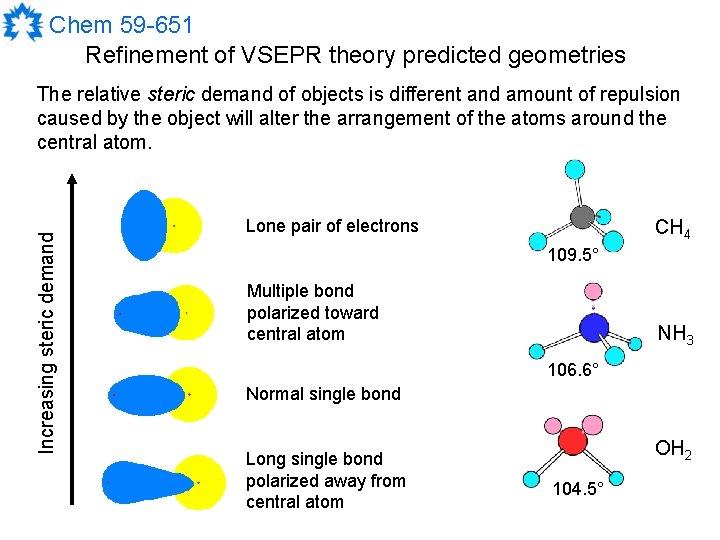
Chem 59 -651 Refinement of VSEPR theory predicted geometries Increasing steric demand The relative steric demand of objects is different and amount of repulsion caused by the object will alter the arrangement of the atoms around the central atom. CH 4 Lone pair of electrons 109. 5° Multiple bond polarized toward central atom NH 3 106. 6° Normal single bond Long single bond polarized away from central atom OH 2 104. 5°

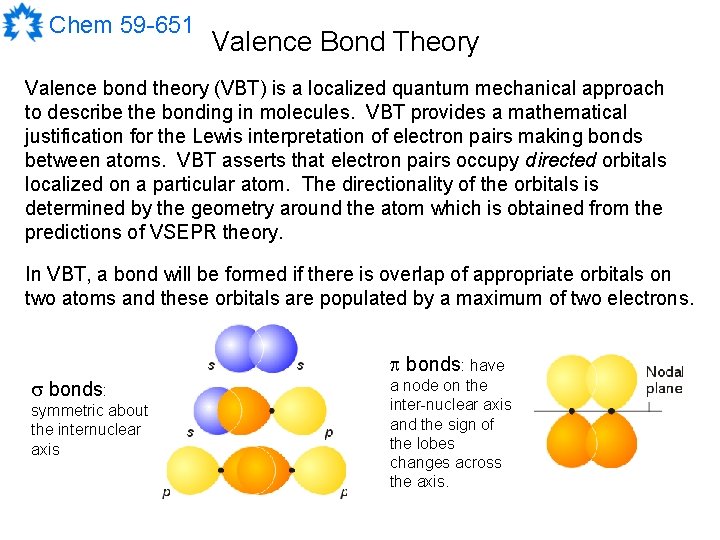
Chem 59 -651 Valence Bond Theory Valence bond theory (VBT) is a localized quantum mechanical approach to describe the bonding in molecules. VBT provides a mathematical justification for the Lewis interpretation of electron pairs making bonds between atoms. VBT asserts that electron pairs occupy directed orbitals localized on a particular atom. The directionality of the orbitals is determined by the geometry around the atom which is obtained from the predictions of VSEPR theory. In VBT, a bond will be formed if there is overlap of appropriate orbitals on two atoms and these orbitals are populated by a maximum of two electrons. bonds: have bonds: symmetric about the internuclear axis a node on the inter-nuclear axis and the sign of the lobes changes across the axis.

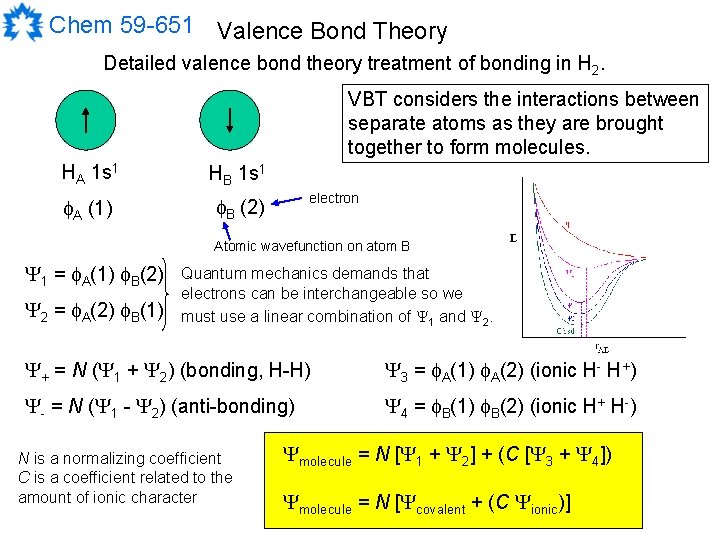
Chem 59 -651 Valence Bond Theory Detailed valence bond theory treatment of bonding in H 2. VBT considers the interactions between separate atoms as they are brought together to form molecules. HA 1 s 1 HB 1 s 1 A (1) B (2) electron Atomic wavefunction on atom B 1 = A(1) B(2) 2 = A(2) B(1) Quantum mechanics demands that electrons can be interchangeable so we must use a linear combination of 1 and 2. + = N ( 1 + 2) (bonding, H-H) 3 = A(1) A(2) (ionic H- H+) - = N ( 1 - 2) (anti-bonding) 4 = B(1) B(2) (ionic H+ H-) N is a normalizing coefficient C is a coefficient related to the amount of ionic character molecule = N [ 1 + 2] + (C [ 3 + 4]) molecule = N [ covalent + (C ionic)]

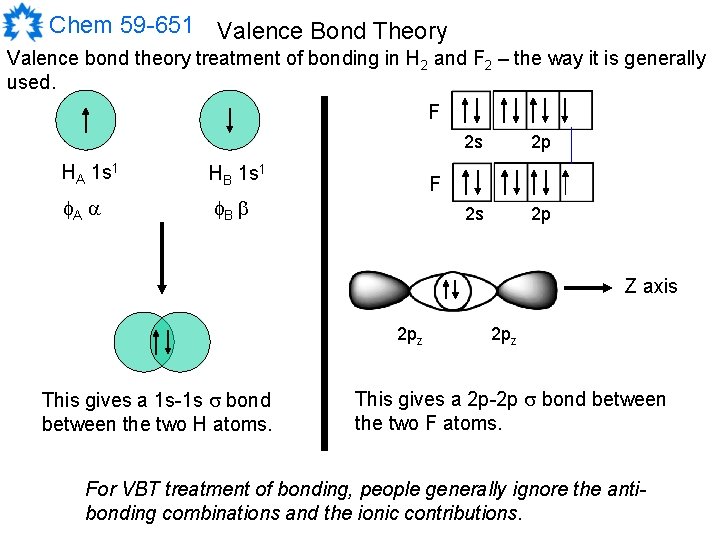
Chem 59 -651 Valence Bond Theory Valence bond theory treatment of bonding in H 2 and F 2 – the way it is generally used. F HA 1 s 1 HB 1 s 1 A a B b 2 s 2 p F Z axis 2 pz This gives a 1 s-1 s bond between the two H atoms. 2 pz This gives a 2 p-2 p bond between the two F atoms. For VBT treatment of bonding, people generally ignore the antibonding combinations and the ionic contributions.

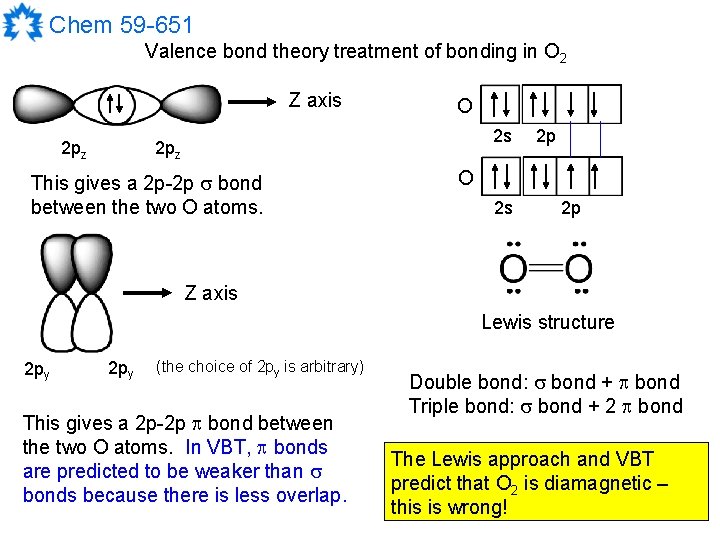
Chem 59 -651 Valence bond theory treatment of bonding in O 2 Z axis 2 pz O 2 s 2 pz This gives a 2 p-2 p bond between the two O atoms. 2 p O 2 s 2 p Z axis Lewis structure 2 py (the choice of 2 py is arbitrary) This gives a 2 p-2 p bond between the two O atoms. In VBT, bonds are predicted to be weaker than bonds because there is less overlap. Double bond: bond + bond Triple bond: bond + 2 bond The Lewis approach and VBT predict that O 2 is diamagnetic – this is wrong!

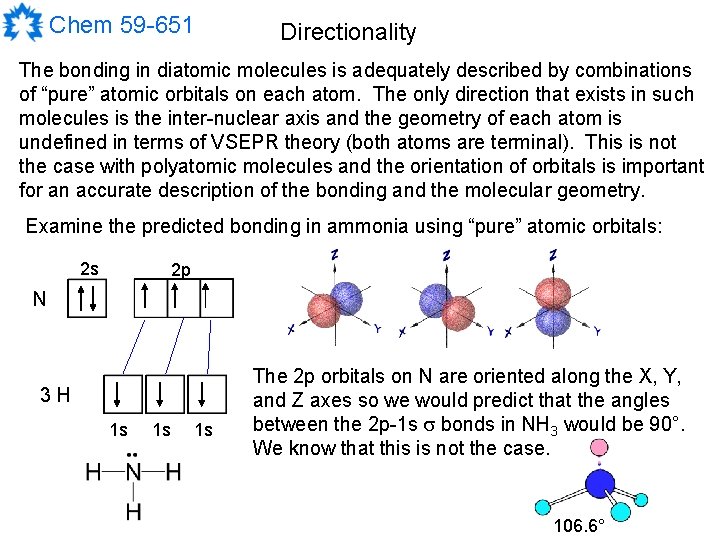
Chem 59 -651 Directionality The bonding in diatomic molecules is adequately described by combinations of “pure” atomic orbitals on each atom. The only direction that exists in such molecules is the inter-nuclear axis and the geometry of each atom is undefined in terms of VSEPR theory (both atoms are terminal). This is not the case with polyatomic molecules and the orientation of orbitals is important for an accurate description of the bonding and the molecular geometry. Examine the predicted bonding in ammonia using “pure” atomic orbitals: 2 s 2 p N 3 H 1 s 1 s 1 s The 2 p orbitals on N are oriented along the X, Y, and Z axes so we would predict that the angles between the 2 p-1 s bonds in NH 3 would be 90°. We know that this is not the case. 106. 6°

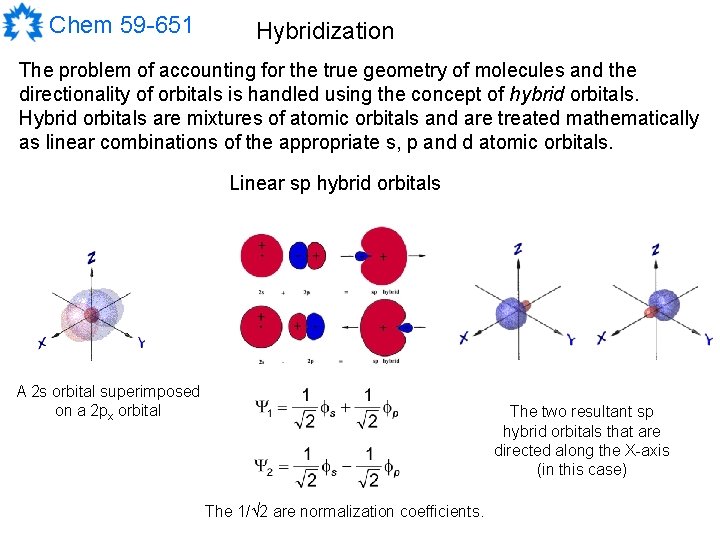
Chem 59 -651 Hybridization The problem of accounting for the true geometry of molecules and the directionality of orbitals is handled using the concept of hybrid orbitals. Hybrid orbitals are mixtures of atomic orbitals and are treated mathematically as linear combinations of the appropriate s, p and d atomic orbitals. Linear sp hybrid orbitals A 2 s orbital superimposed on a 2 px orbital The two resultant sp hybrid orbitals that are directed along the X-axis (in this case) The 1/ 2 are normalization coefficients.

Chem 59 -651 Orthogonality and Normalization Two properties of acceptable orbitals (wavefunctions) that we have not yet considered are that they must be orthogonal to every other orbital and they must be normalized. These conditions are related to the probability of finding an electron in a given space. Orthogonal means that the integral of the product of an orbital with any other orbital is equal to 0, i. e. : where n m and dt means that the integral is taken over “all of space” (everywhere). Normal means that the integral of the product of an orbital with itself is equal to 1, i. e. : This means that we must find normalization coefficients that satisfy these conditions. Note that the atomic orbitals ( ) we use can be considered to be both orthogonal and normal or “orthonormal”.

Chem 59 -651 Example of the orthogonality of 1 and 2 Thus our hybrid sp orbitals are orthogonal to each other, as required.

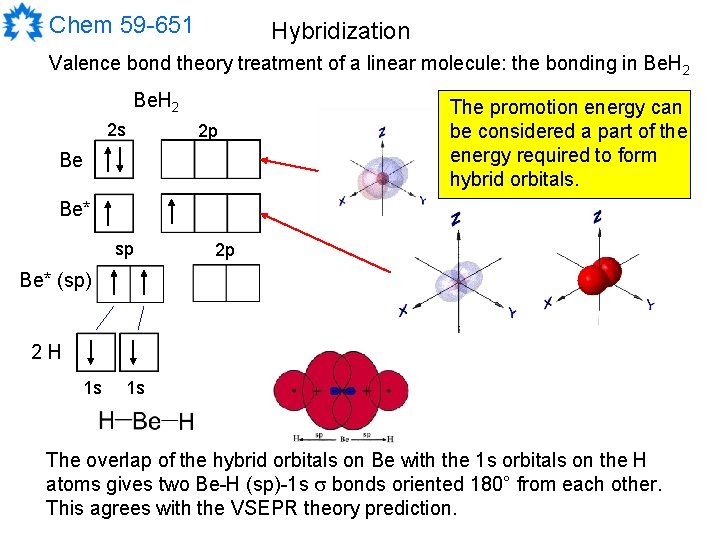
Chem 59 -651 Hybridization Valence bond theory treatment of a linear molecule: the bonding in Be. H 2 2 s 2 p Be The promotion energy can be considered a part of the energy required to form hybrid orbitals. Be* sp 2 p Be* (sp) 2 H 1 s 1 s The overlap of the hybrid orbitals on Be with the 1 s orbitals on the H atoms gives two Be-H (sp)-1 s bonds oriented 180° from each other. This agrees with the VSEPR theory prediction.

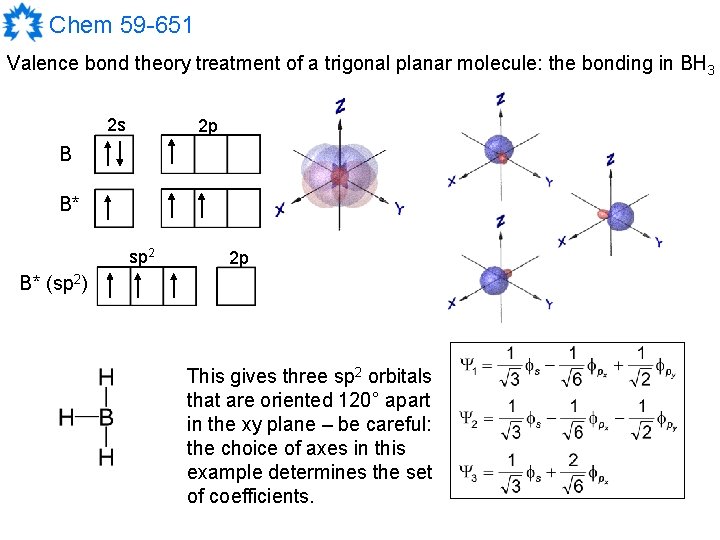
Chem 59 -651 Valence bond theory treatment of a trigonal planar molecule: the bonding in BH 3 2 s 2 p B B* sp 2 2 p B* (sp 2) This gives three sp 2 orbitals that are oriented 120° apart in the xy plane – be careful: the choice of axes in this example determines the set of coefficients.

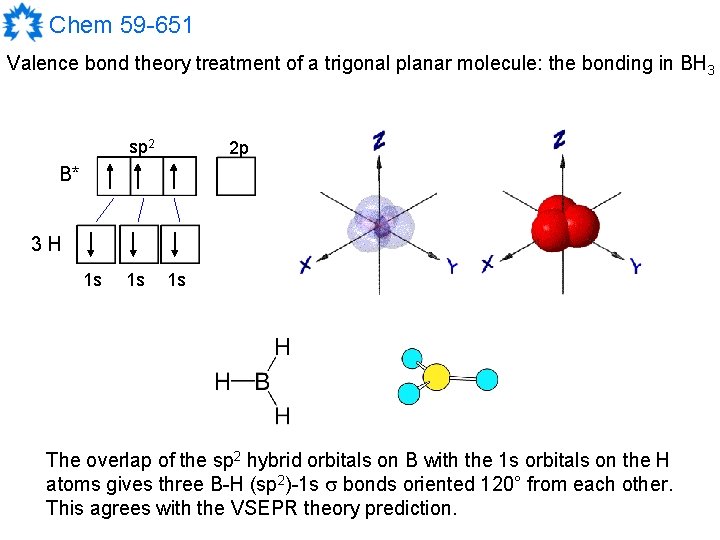
Chem 59 -651 Valence bond theory treatment of a trigonal planar molecule: the bonding in BH 3 sp 2 2 p B* 3 H 1 s 1 s 1 s The overlap of the sp 2 hybrid orbitals on B with the 1 s orbitals on the H atoms gives three B-H (sp 2)-1 s bonds oriented 120° from each other. This agrees with the VSEPR theory prediction.

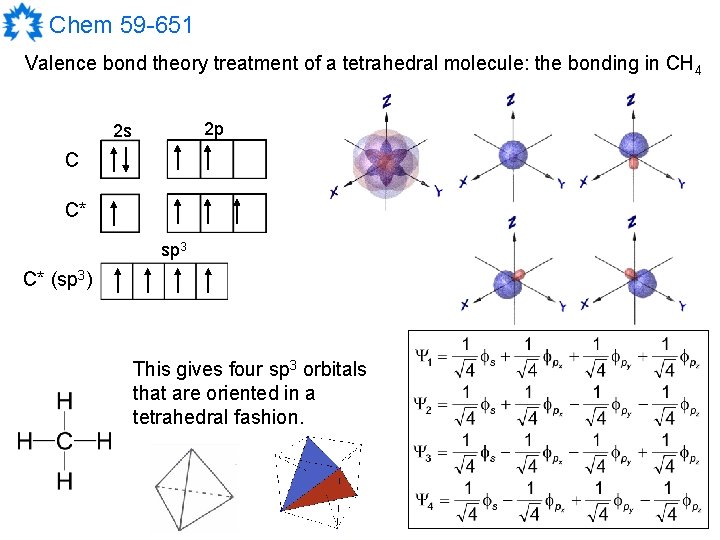
Chem 59 -651 Valence bond theory treatment of a tetrahedral molecule: the bonding in CH 4 2 p 2 s C C* sp 3 C* (sp 3) This gives four sp 3 orbitals that are oriented in a tetrahedral fashion.

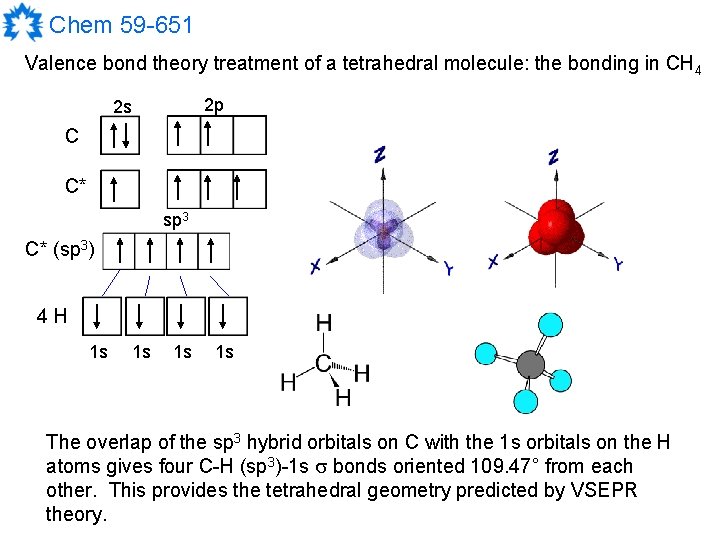
Chem 59 -651 Valence bond theory treatment of a tetrahedral molecule: the bonding in CH 4 2 p 2 s C C* sp 3 C* (sp 3) 4 H 1 s 1 s The overlap of the sp 3 hybrid orbitals on C with the 1 s orbitals on the H atoms gives four C-H (sp 3)-1 s bonds oriented 109. 47° from each other. This provides the tetrahedral geometry predicted by VSEPR theory.

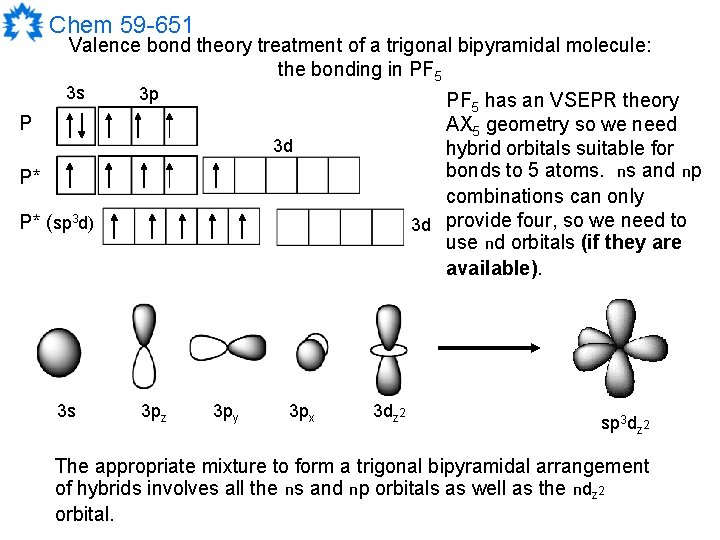
Chem 59 -651 Valence bond theory treatment of a trigonal bipyramidal molecule: the bonding in PF 5 3 s 3 p PF 5 has an VSEPR theory AX 5 geometry so we need hybrid orbitals suitable for bonds to 5 atoms. ns and np combinations can only 3 d provide four, so we need to use nd orbitals (if they are available). P 3 d P* P* (sp 3 d) 3 s 3 pz 3 py 3 px 3 dz 2 sp 3 dz 2 The appropriate mixture to form a trigonal bipyramidal arrangement of hybrids involves all the ns and np orbitals as well as the ndz 2 orbital.

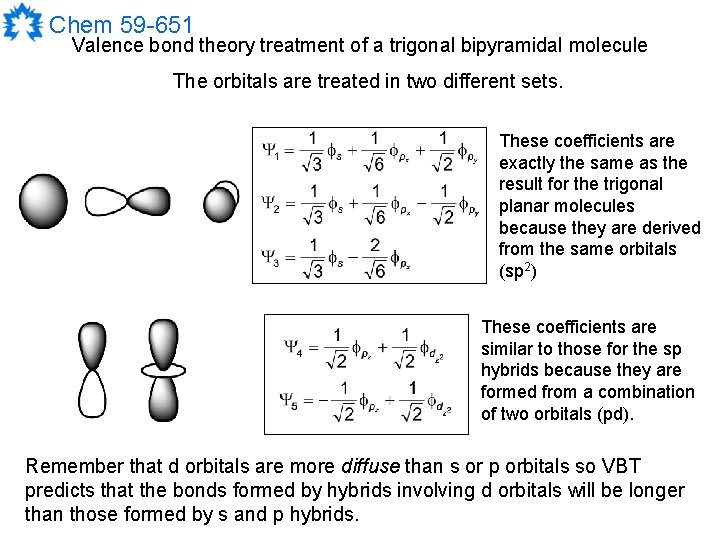
Chem 59 -651 Valence bond theory treatment of a trigonal bipyramidal molecule The orbitals are treated in two different sets. These coefficients are exactly the same as the result for the trigonal planar molecules because they are derived from the same orbitals (sp 2) These coefficients are similar to those for the sp hybrids because they are formed from a combination of two orbitals (pd). Remember that d orbitals are more diffuse than s or p orbitals so VBT predicts that the bonds formed by hybrids involving d orbitals will be longer than those formed by s and p hybrids.

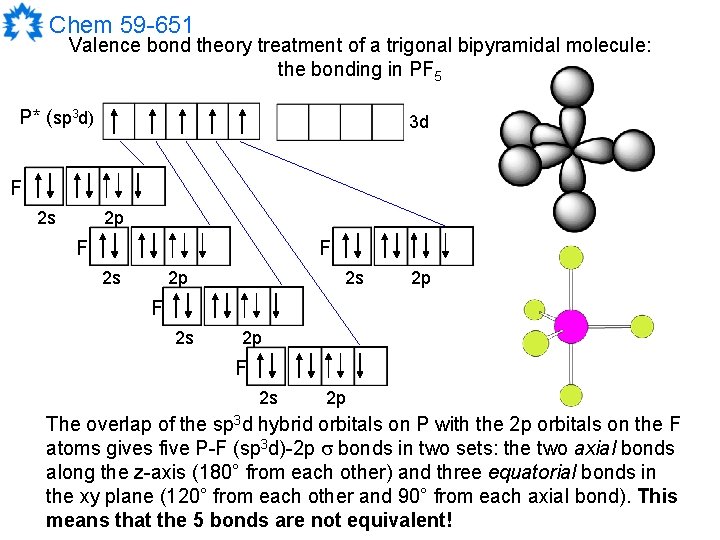
Chem 59 -651 Valence bond theory treatment of a trigonal bipyramidal molecule: the bonding in PF 5 P* (sp 3 d) 3 d F 2 s 2 p F 2 s 2 p The overlap of the sp 3 d hybrid orbitals on P with the 2 p orbitals on the F atoms gives five P-F (sp 3 d)-2 p bonds in two sets: the two axial bonds along the z-axis (180° from each other) and three equatorial bonds in the xy plane (120° from each other and 90° from each axial bond). This means that the 5 bonds are not equivalent!

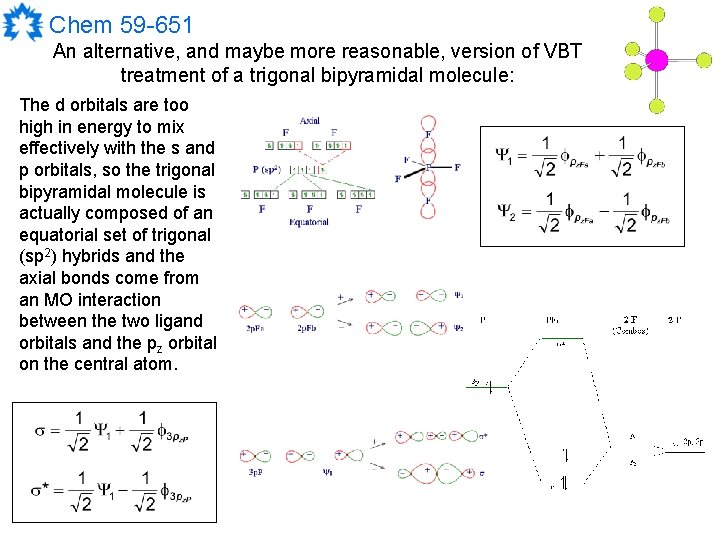
Chem 59 -651 An alternative, and maybe more reasonable, version of VBT treatment of a trigonal bipyramidal molecule: The d orbitals are too high in energy to mix effectively with the s and p orbitals, so the trigonal bipyramidal molecule is actually composed of an equatorial set of trigonal (sp 2) hybrids and the axial bonds come from an MO interaction between the two ligand orbitals and the pz orbital on the central atom.

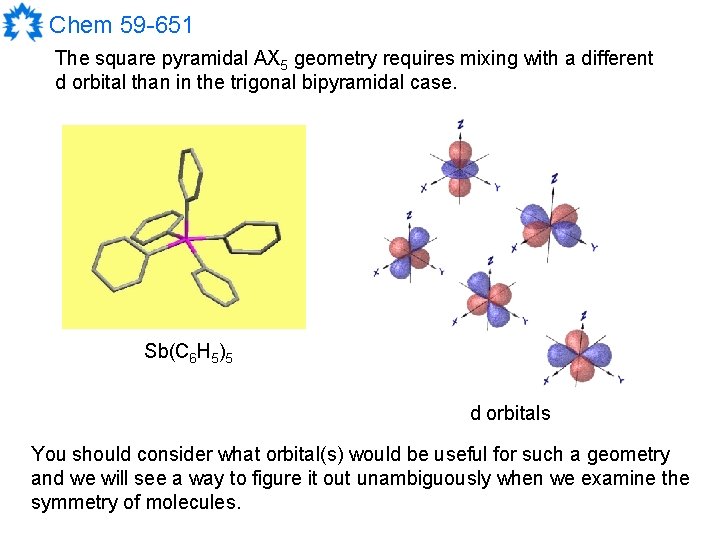
Chem 59 -651 The square pyramidal AX 5 geometry requires mixing with a different d orbital than in the trigonal bipyramidal case. Sb(C 6 H 5)5 d orbitals You should consider what orbital(s) would be useful for such a geometry and we will see a way to figure it out unambiguously when we examine the symmetry of molecules.

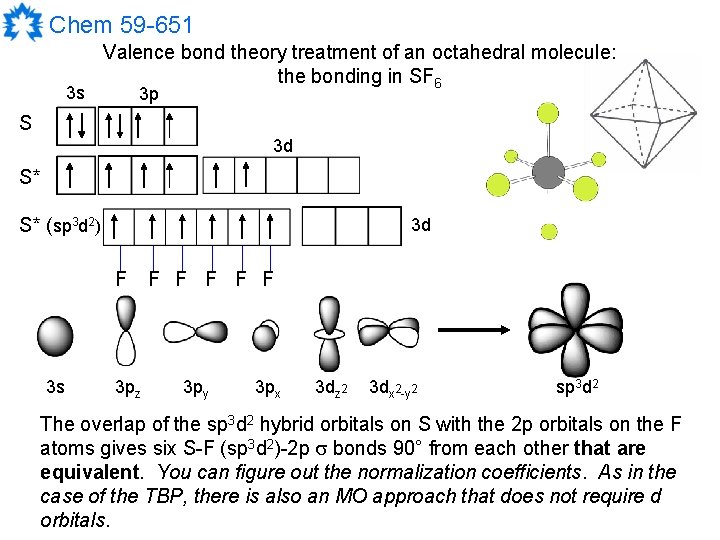
Chem 59 -651 3 s Valence bond theory treatment of an octahedral molecule: the bonding in SF 6 3 p S 3 d S* S* (sp 3 d 2) 3 d F 3 s 3 pz F F F 3 py 3 px 3 dz 2 3 dx 2 -y 2 sp 3 d 2 The overlap of the sp 3 d 2 hybrid orbitals on S with the 2 p orbitals on the F atoms gives six S-F (sp 3 d 2)-2 p bonds 90° from each other that are equivalent. You can figure out the normalization coefficients. As in the case of the TBP, there is also an MO approach that does not require d orbitals.

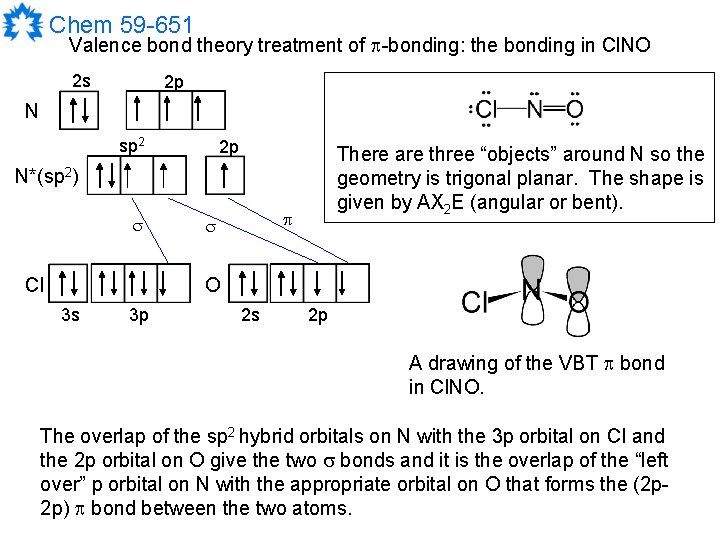
Chem 59 -651 Valence bond theory treatment of -bonding: the bonding in Cl. NO 2 s 2 p N sp 2 2 p There are three “objects” around N so the geometry is trigonal planar. The shape is given by AX 2 E (angular or bent). N*(sp 2) Cl O 3 s 3 p 2 s 2 p A drawing of the VBT bond in Cl. NO. The overlap of the sp 2 hybrid orbitals on N with the 3 p orbital on Cl and the 2 p orbital on O give the two bonds and it is the overlap of the “left over” p orbital on N with the appropriate orbital on O that forms the (2 p 2 p) bond between the two atoms.

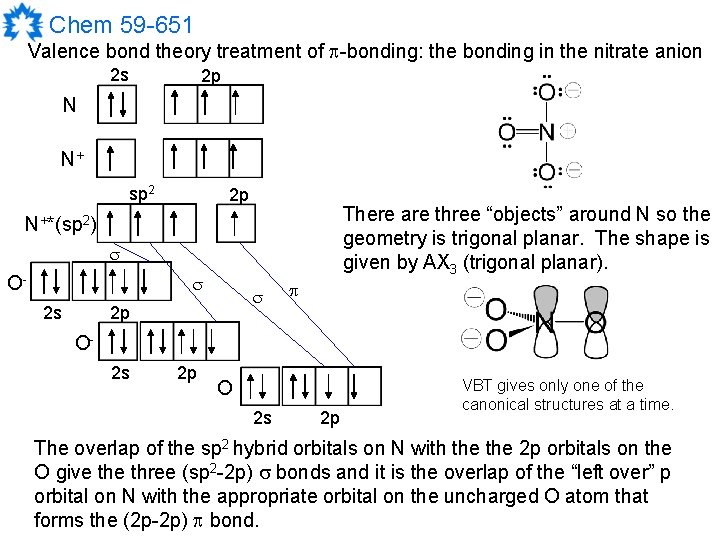
Chem 59 -651 Valence bond theory treatment of -bonding: the bonding in the nitrate anion 2 s 2 p N N+ sp 2 2 p There are three “objects” around N so the geometry is trigonal planar. The shape is given by AX 3 (trigonal planar). N+*(sp 2) O 2 s 2 p VBT gives only one of the canonical structures at a time. The overlap of the sp 2 hybrid orbitals on N with the 2 p orbitals on the O give three (sp 2 -2 p) bonds and it is the overlap of the “left over” p orbital on N with the appropriate orbital on the uncharged O atom that forms the (2 p-2 p) bond.

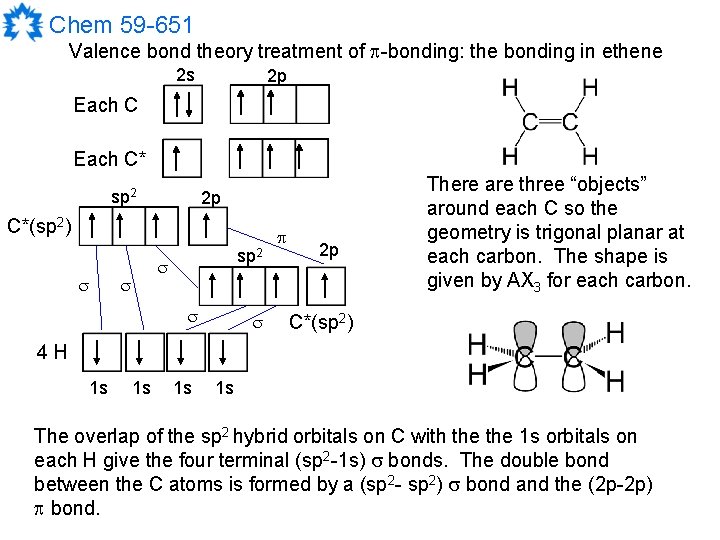
Chem 59 -651 Valence bond theory treatment of -bonding: the bonding in ethene 2 s 2 p Each C* sp 2 2 p C*(sp 2) sp 2 2 p There are three “objects” around each C so the geometry is trigonal planar at each carbon. The shape is given by AX 3 for each carbon. C*(sp 2) 4 H 1 s 1 s The overlap of the sp 2 hybrid orbitals on C with the 1 s orbitals on each H give the four terminal (sp 2 -1 s) bonds. The double bond between the C atoms is formed by a (sp 2 - sp 2) bond and the (2 p-2 p) bond.

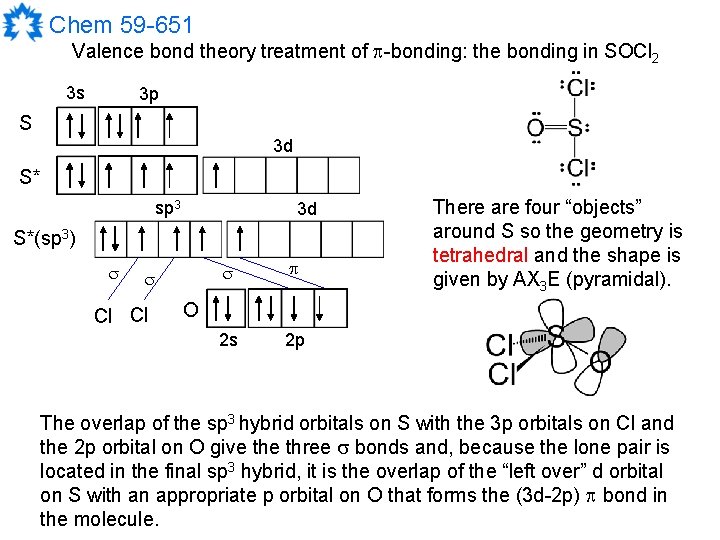
Chem 59 -651 Valence bond theory treatment of -bonding: the bonding in SOCl 2 3 s 3 p S 3 d S* sp 3 3 d S*(sp 3) Cl Cl 2 s 2 p There are four “objects” around S so the geometry is tetrahedral and the shape is given by AX 3 E (pyramidal). O The overlap of the sp 3 hybrid orbitals on S with the 3 p orbitals on Cl and the 2 p orbital on O give three bonds and, because the lone pair is located in the final sp 3 hybrid, it is the overlap of the “left over” d orbital on S with an appropriate p orbital on O that forms the (3 d-2 p) bond in the molecule.

Chem 59 -651 Valence bond theory treatment of bonding: a hypervalent molecule, Cl. F 3 3 s 3 p Cl 3 d Cl* (sp 3 d) 3 d F F F There are five “objects” around Cl so the geometry is trigonal bipyramidal and the shape is given by AX 3 E 2 (T-shaped). Consider this: Why are such molecules T-shaped instead of pyramidal? The overlap of the sp 3 d hybrid orbitals on Cl with the 2 p orbitals on the F atoms gives three P-F (sp 3 d)-2 p bonds in two sets: the two axial bonds along the z-axis (less than 180° from each other because of the repulsion from the lone pairs) and the one equatorial bond halfway between the other Cl bonds. Again, the bond lengths will not be the same because there is more d contribution to the axial hybrid orbitals.

Chem 59 -651 Summary of Valence Bond Theory 1. Write an acceptable Lewis structure for the molecule. 2. Determine the number of VSEPR objects around all central atoms and determine the geometry around the atom. 3. Construct hybrid orbitals suitable for the predicted bonding. 4. Link orbitals together to make bonds. 5. Describe the bonding. Include the names of the orbitals involved in each bond. Draw pictures of the bonds formed by the overlap of these orbitals. Two objects around Be, so AX 2 (linear) Two orbitals pointing 180° from each other needed, so use two sp hybrids sp Two (sp-1 s) Be-H bonds. 1 s