CHEM 515 Spectroscopy Vibrational Spectroscopy II Vibrations of

CHEM 515 Spectroscopy Vibrational Spectroscopy II

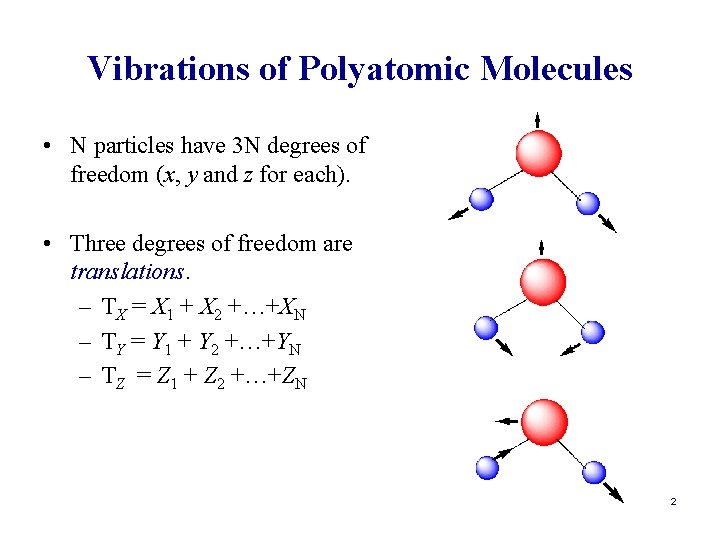
Vibrations of Polyatomic Molecules • N particles have 3 N degrees of freedom (x, y and z for each). • Three degrees of freedom are translations. – TX = X 1 + X 2 +…+XN – TY = Y 1 + Y 2 +…+YN – TZ = Z 1 + Z 2 +…+ZN 2

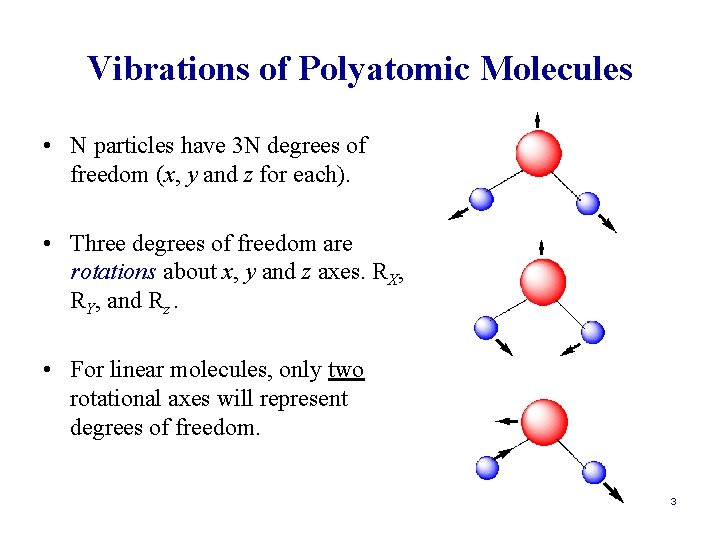
Vibrations of Polyatomic Molecules • N particles have 3 N degrees of freedom (x, y and z for each). • Three degrees of freedom are rotations about x, y and z axes. RX, RY, and Rz. • For linear molecules, only two rotational axes will represent degrees of freedom. 3

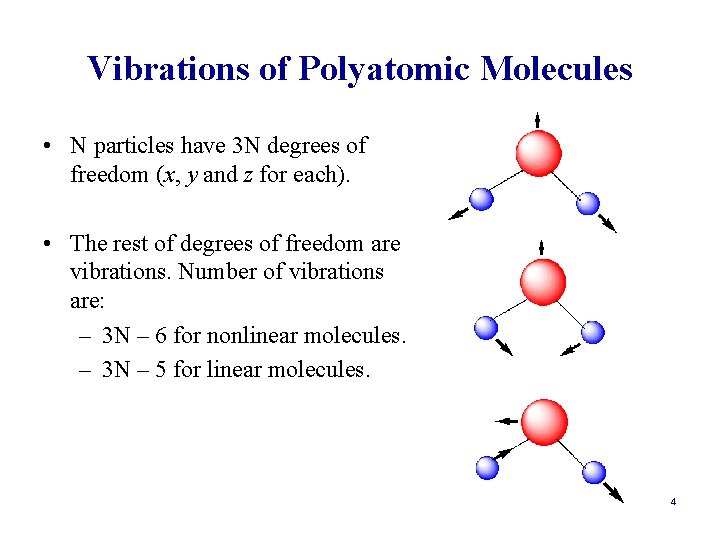
Vibrations of Polyatomic Molecules • N particles have 3 N degrees of freedom (x, y and z for each). • The rest of degrees of freedom are vibrations. Number of vibrations are: – 3 N – 6 for nonlinear molecules. – 3 N – 5 for linear molecules. 4

Classical Picture of Vibrational Motions in Molecules • Classically, polyatomic molecules can be considered as a set of coupled harmonic oscillators. • Atoms are shown as balls connected with each other by Hooke’s law springs. 5

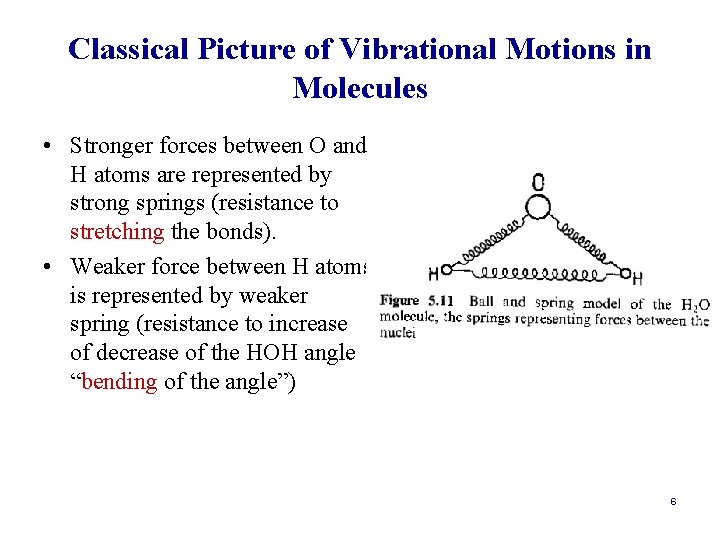
Classical Picture of Vibrational Motions in Molecules • Stronger forces between O and H atoms are represented by strong springs (resistance to stretching the bonds). • Weaker force between H atoms is represented by weaker spring (resistance to increase of decrease of the HOH angle “bending of the angle”) 6

Normal Modes of Vibrations • The collective motion of the atoms, sometimes called Lissajous motion, in a molecule can be decomposed into normal modes of vibration within the harmonic approximation. 7

Normal Modes of Vibrations • The normal modes are mutually orthogonal. That is they represent linearly independent motions of the nuclei about the center-of-mass of the molecule. • For CO 2 molecule, number of vibrations = 3 N – 5 = four vibrations. 8

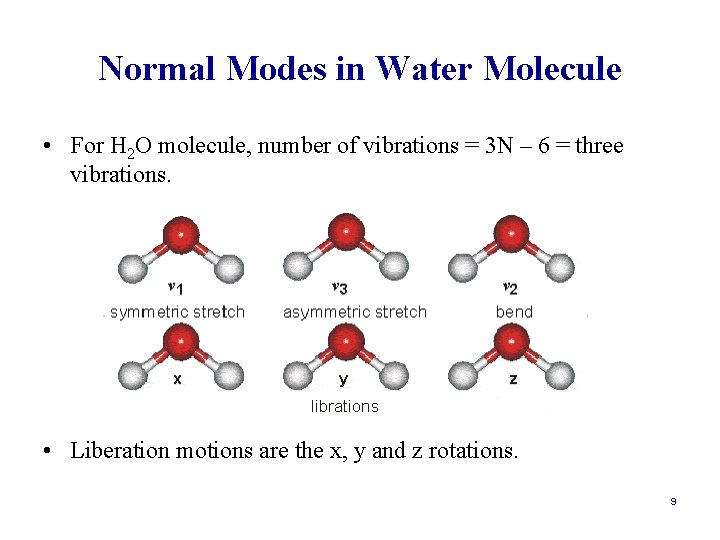
Normal Modes in Water Molecule • For H 2 O molecule, number of vibrations = 3 N – 6 = three vibrations. • Liberation motions are the x, y and z rotations. 9

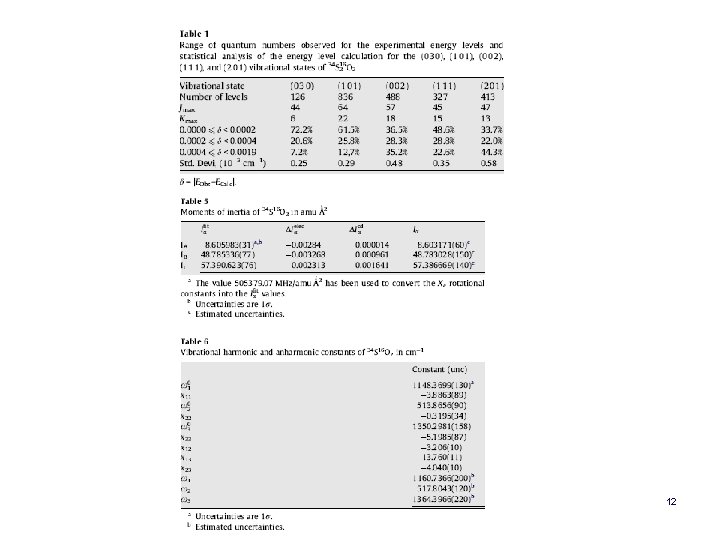
Vibrational Energy levels for H 2 O 10

11

12