Chem 302 Math 252 Chapter 5 Regression Linear



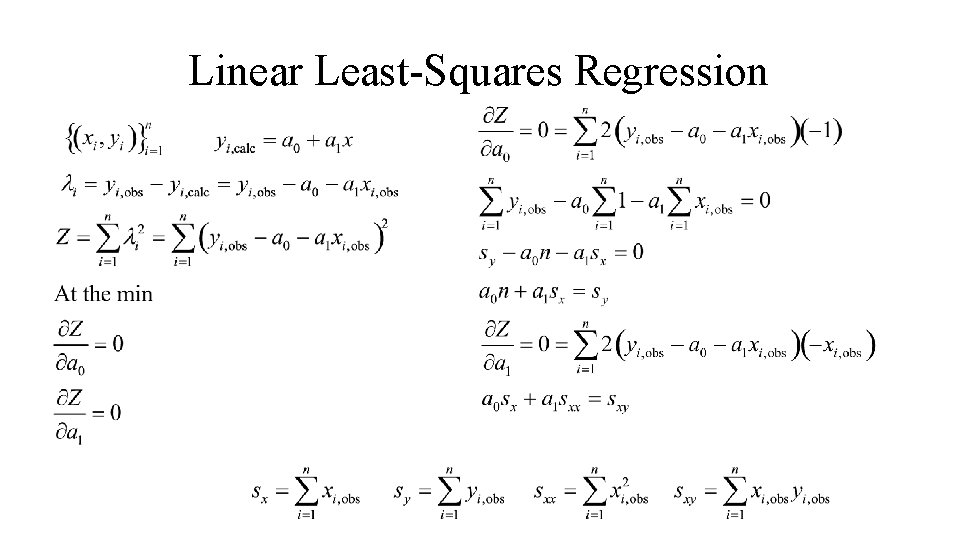



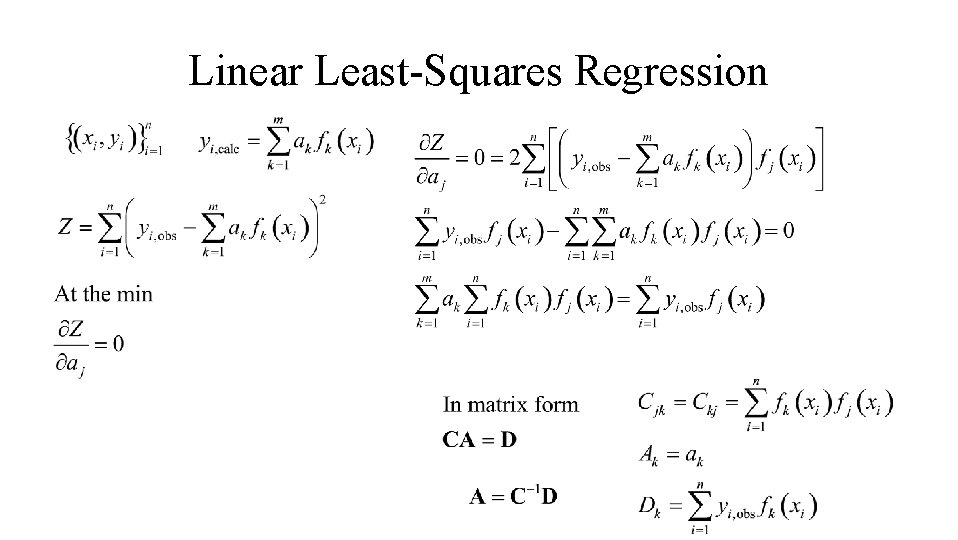


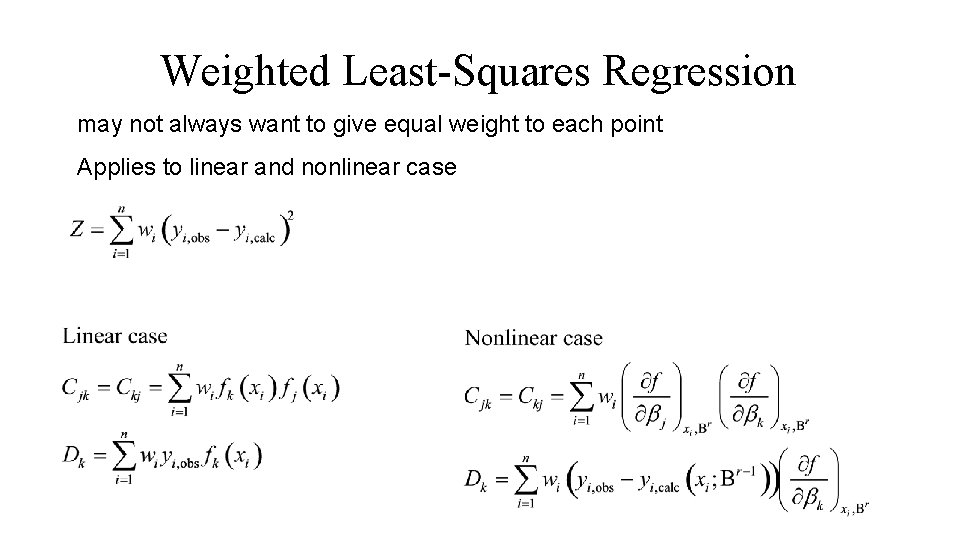








- Slides: 27

Chem 302 - Math 252 Chapter 5 Regression

Linear & Nonlinear Regression • Linear regression – Linear in the parameters – Does not have to be linear in the independent variable(s) – Can be solved through a system of linear equations • Nonlinear – Nonlinear in parameters – Usually requires linearization and iteration

Linear Least-Squares Regression Residual Sum of Square Residuals Want to minimize Z
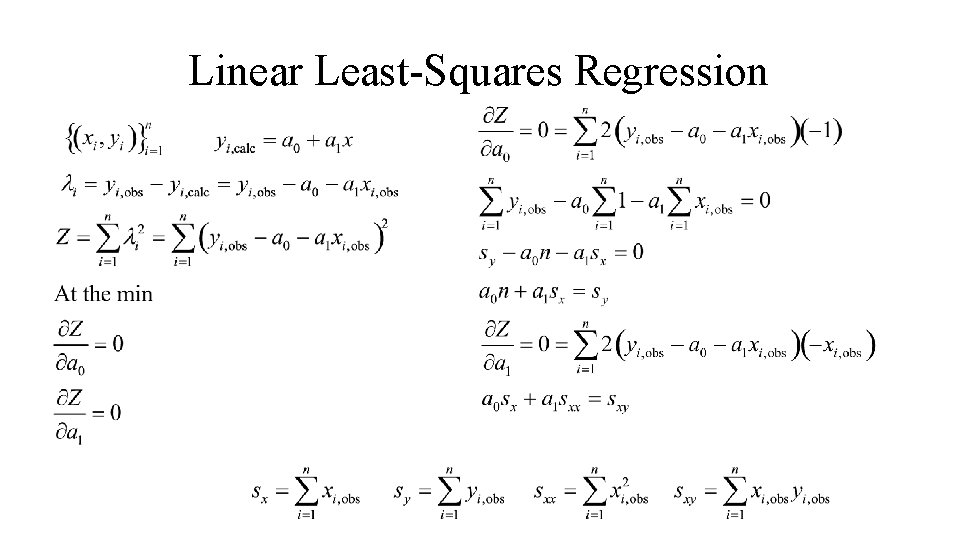
Linear Least-Squares Regression

Linear Least-Squares Regression Example

Linear Least-Squares Regression Uncertainties in Parameters Example

Linear Least-Squares Regression on “y” Treat x as y and y as x Choose x as variable with smallest error Can also be determined by equation
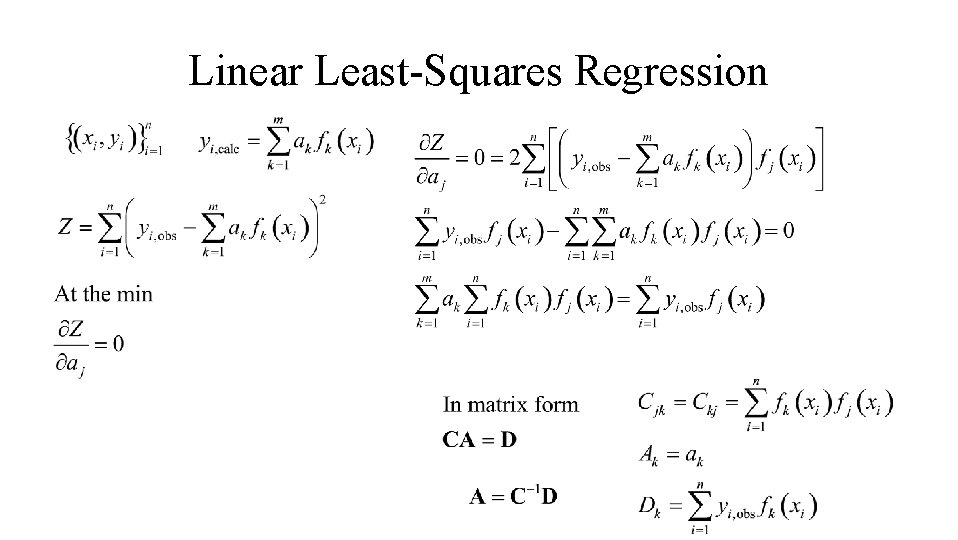
Linear Least-Squares Regression

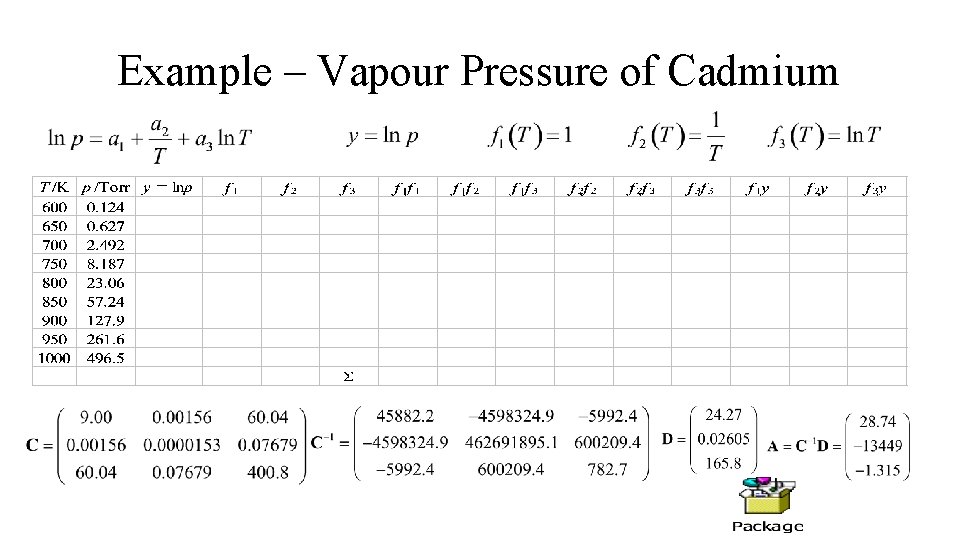
Example – Vapour Pressure of Cadmium

Linear Least-Squares Regression Uncertainties in Parameters

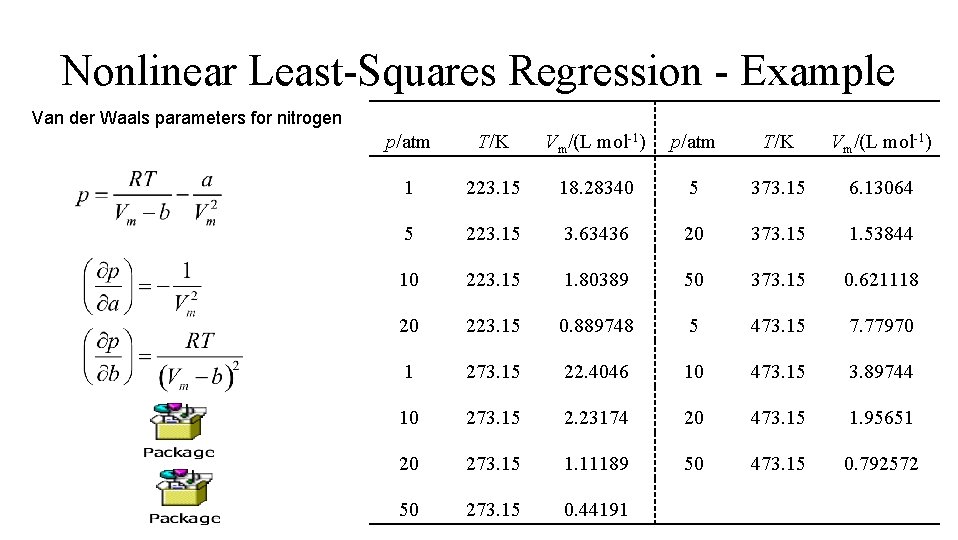
Nonlinear Least-Squares Regression This results in a system of nonlinear equations Linearize & solve iteratively Need initial estimate of parameters

Nonlinear Least-Squares Regression - Example Van der Waals parameters for nitrogen p/atm T/K Vm/(L mol-1) 1 223. 15 18. 28340 5 373. 15 6. 13064 5 223. 15 3. 63436 20 373. 15 1. 53844 10 223. 15 1. 80389 50 373. 15 0. 621118 20 223. 15 0. 889748 5 473. 15 7. 77970 1 273. 15 22. 4046 10 473. 15 3. 89744 10 273. 15 2. 23174 20 473. 15 1. 95651 20 273. 15 1. 11189 50 473. 15 0. 792572 50 273. 15 0. 44191
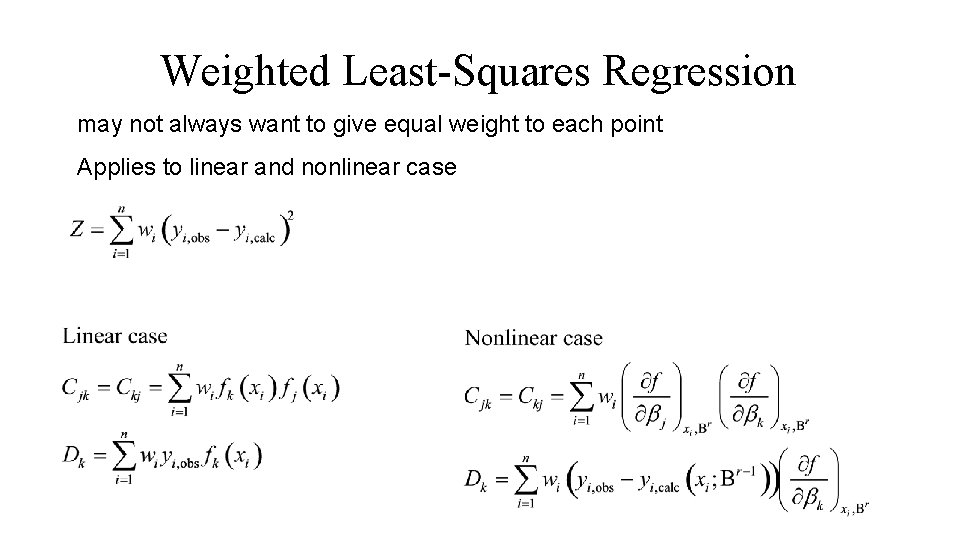
Weighted Least-Squares Regression may not always want to give equal weight to each point Applies to linear and nonlinear case

Drawbacks of Iterative Matrix Method • Local minima can cause problems • Can be sensitive to initial guess • Derivatives must be evaluated for each iteration

Simplex Method • Simplex has one more vertex than dimension of space – 2 D – Triangle • • m parameters – m+1 vertices Simplex Method used to optimize a set of parameters – Find optimal set of b’s such that Z is minimum • More robust than previous iterative procedure – Often slower

Simplex Method 1. Evaluate Z at m+1 unique sets of parameters 2. Identify ZB (best, smallest) and ZW (worst, largest) 3. Calculate Centroid of all but worst (average of different sets of parameters ignoring worst set) 4. Reflect worst point through Centroid

Simplex Method 5. Replace Worst point: a. If ZR 1<ZB (reflected point is better than previous best) calculate i. If ZR 2<ZR 1 replace W with R 2 ii. Otherwise replace W with R 1 b. If ZB<ZR 1<ZW replace W with R 1 c. If ZR 1>ZW a contracted point id calculated i. If ZR 3<ZW replace W with R 3 ii. Otherwise move all points closer to the best point 6. Repeat until converged or maximum number of iterations have been performed

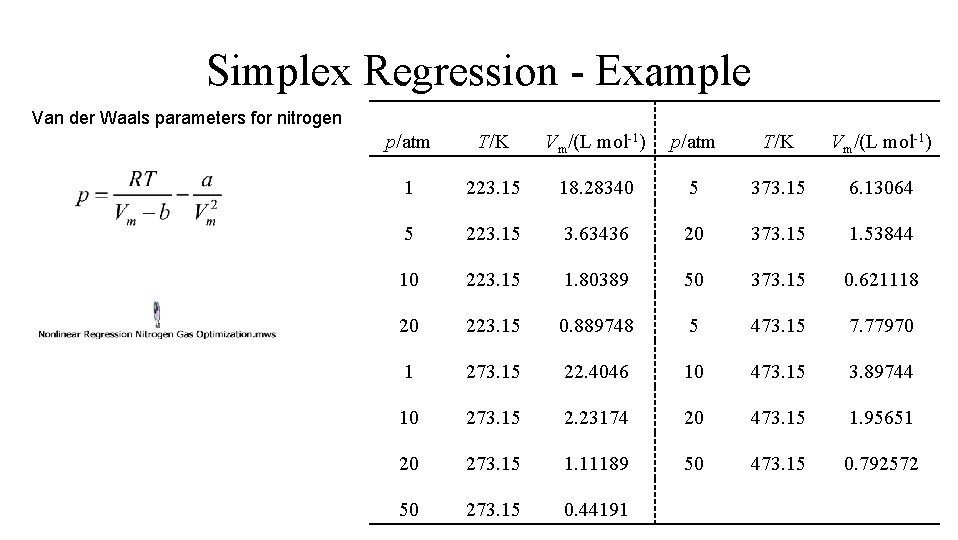
Simplex Regression - Example Van der Waals parameters for nitrogen p/atm T/K Vm/(L mol-1) 1 223. 15 18. 28340 5 373. 15 6. 13064 5 223. 15 3. 63436 20 373. 15 1. 53844 10 223. 15 1. 80389 50 373. 15 0. 621118 20 223. 15 0. 889748 5 473. 15 7. 77970 1 273. 15 22. 4046 10 473. 15 3. 89744 10 273. 15 2. 23174 20 473. 15 1. 95651 20 273. 15 1. 11189 50 473. 15 0. 792572 50 273. 15 0. 44191

Simplex program

Iteration 1: Response 0. 344652 beta Response 1. 300000 0. 050000 0. 425437 1. 326000 0. 050500 0. 344652 1. 313000 0. 051000 0. 579697 1. 313000 0. 050250 1. 313000 0. 049500 0. 229741 1. 313000 0. 048750 0. 116962 Iteration 2: Response 0. 116962 beta Response 1. 300000 0. 050000 0. 425437 1. 326000 0. 050500 0. 344652 1. 313000 0. 048750 0. 116962 1. 319500 0. 049625 1. 339000 0. 049250 0. 076378 1. 358500 0. 048875 0. 011665 Iteration 3: Response 0. 0116649 beta Response 1. 358500 0. 048875 0. 011665 1. 326000 0. 050500 0. 344652 1. 313000 0. 048750 0. 116962 1. 335750 0. 048812 1. 345500 0. 047125 0. 041013 Iteration 4: Response 0. 0116649 beta Response 1. 358500 0. 048875 0. 011665 1. 345500 0. 047125 0. 041013 1. 313000 0. 048750 0. 116962 1. 352000 0. 048000 1. 391000 0. 047250 0. 195042 1. 332500 0. 048375 0. 027212 Simplex - Example Best Worst Centroid First reflected point Second reflected point Worst Best Centroid First reflected point Second reflected point Best Worst Centroid First reflected point Contracted point Iteration 31: Response 0. 00543252 beta Response 1. 393487 0. 049624 0. 005433 1. 393340 0. 049619 0. 005433 1. 393220 0. 049616 0. 005433 1. 393413 0. 049621 1. 393607 0. 049627 0. 005433 1. 393317 0. 049619 0. 005433 Iteration 32: Response 0. 00543252 beta Response 1. 393487 0. 049624 0. 005433 1. 393340 0. 049619 0. 005433 1. 393317 0. 049619 0. 005433 1. 393328 0. 049619 1. 393170 0. 049613 0. 005433 1. 393408 0. 049621 0. 005433 Iterations converged. R^2 0. 999999 Final Converged Parameters k beta 0 1. 39332 1 0. 0496186 Best Worst Centroid First reflected point Contracted point Worst Best Centroid First reflected point Contracted point

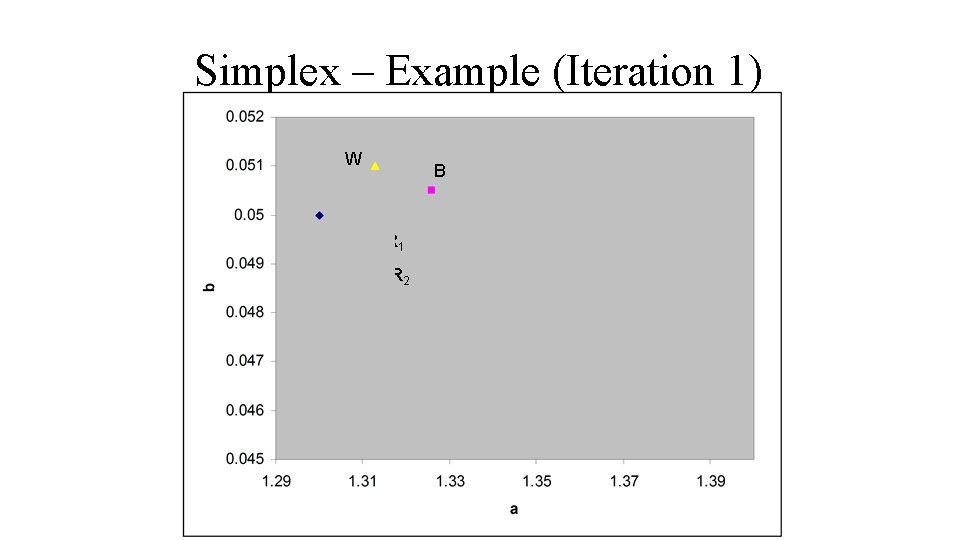
Simplex – Example (Iteration 1) W B C R 1 R 2

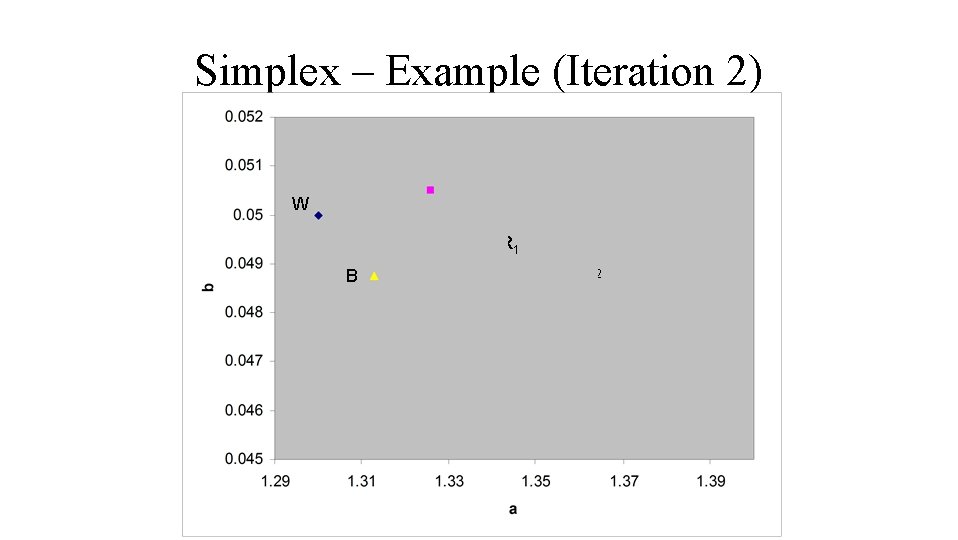
Simplex – Example (Iteration 2) W C B R 1 R 2

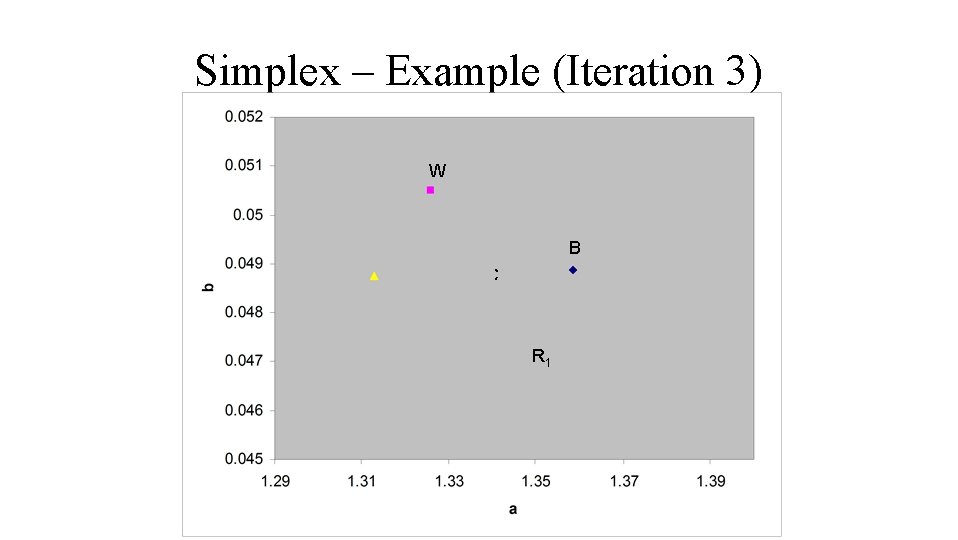
Simplex – Example (Iteration 3) W B C R 1

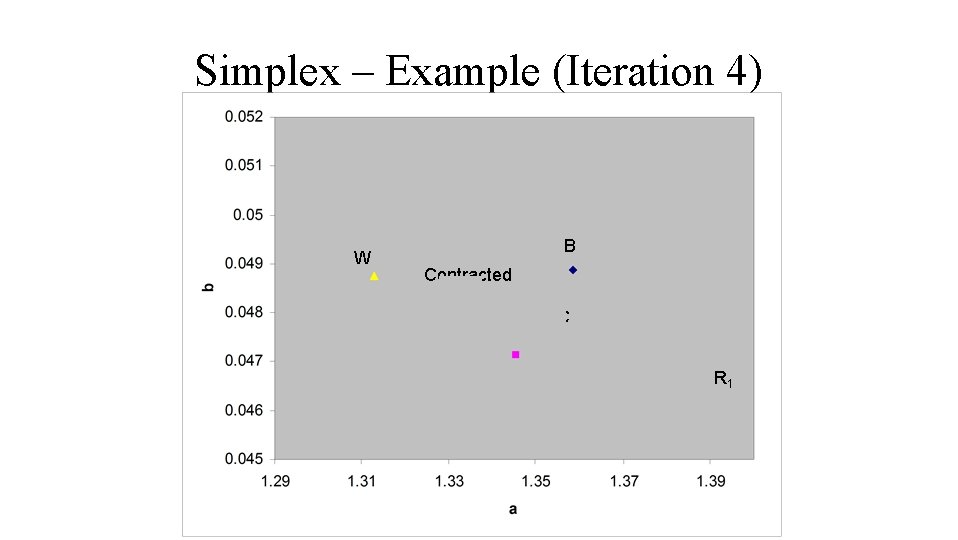
Simplex – Example (Iteration 4) W B Contracted C R 1

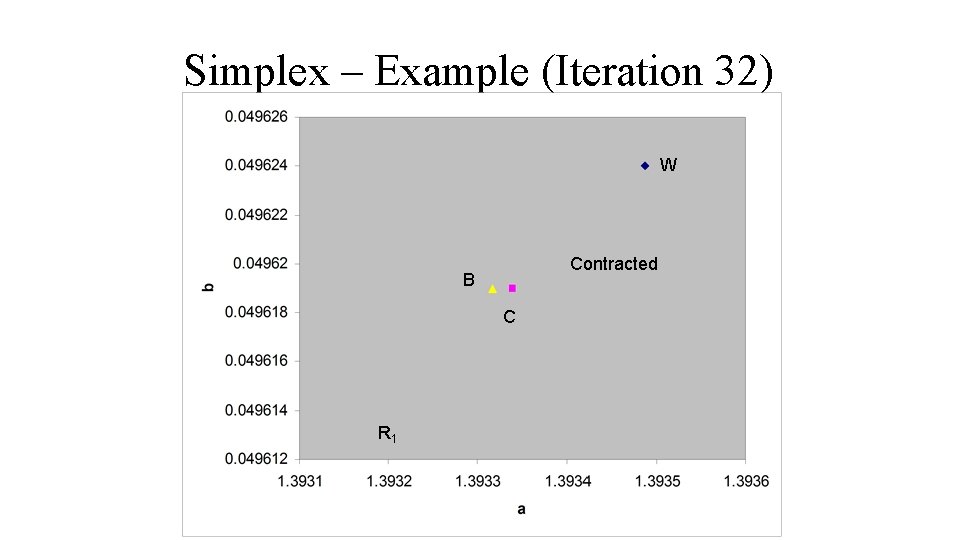
Simplex – Example (Iteration 32) W Contracted B C R 1

Comparing Models • Often have more than 1 equation that can be used to represent the data • If two equations (models) have the same number of parameters the one with smaller Z is a better representation (fit) • If two models have different number of parameters then can not do a direct comparison – Need to use F distribution & Confidence level – Model A – fewer number of parameters Model B – larger number of parameters

Comparing Models Model B is a better model if (and only if) Usually lookup F in Table and compare ratios With Maple can calculate confidence level for which B is a better model than A