Chem 101 Chapter 01 Chemical Foundations 1 What

Chem 101 Chapter 01 Chemical Foundations 1

What is chemistry? The science that explains: the properties of materials how new materials may be made the relationship between energy and chemical reactions how materials may be analyzed at the atomic and molecular level (Macroscopic & Microscopic. A key concept is that chemists look for explanations 2

1. 1 Chemistry: An overview • Chemistry is fundamentally concerned with: "How one substance changes to another" 1. How plants grow by absorbing water and Carbon dioxide? 2. How humans manufacture the proteins from the food we consume? 3. …. . and on • A substance is composed of atoms, all universe is made of only 110 {different types of atoms} 3

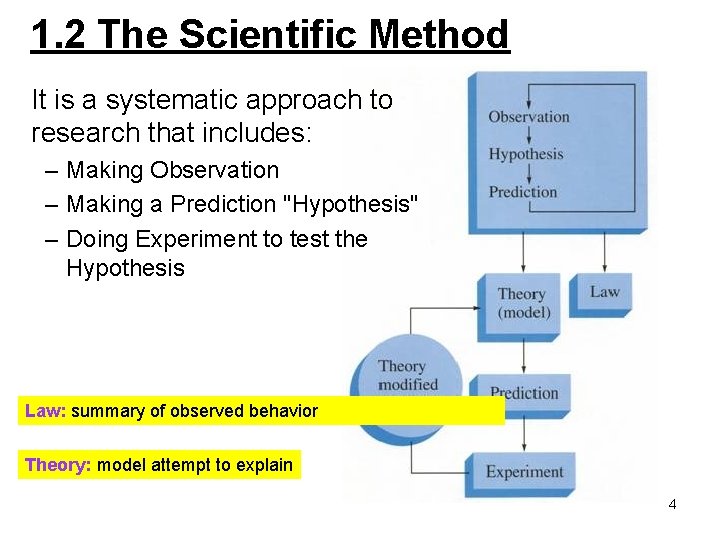
1. 2 The Scientific Method It is a systematic approach to research that includes: – Making Observation – Making a Prediction "Hypothesis" – Doing Experiment to test the Hypothesis Law: summary of observed behavior Theory: model attempt to explain 4

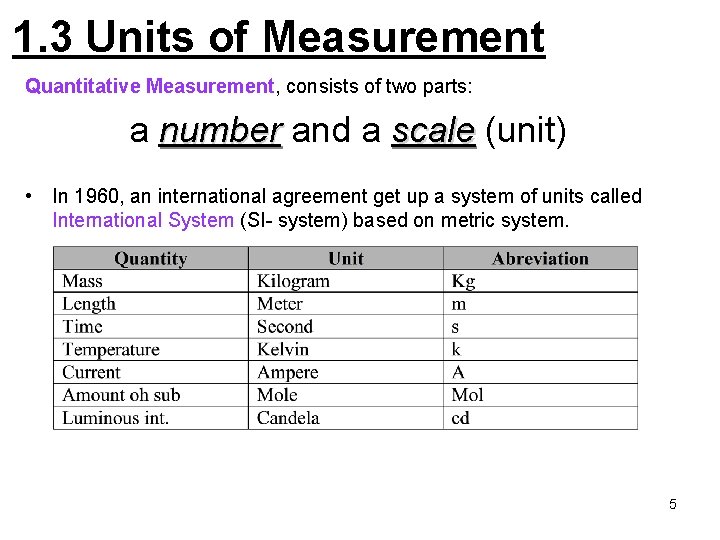
1. 3 Units of Measurement Quantitative Measurement, consists of two parts: a number and a scale (unit) • In 1960, an international agreement get up a system of units called International System (SI- system) based on metric system. 5

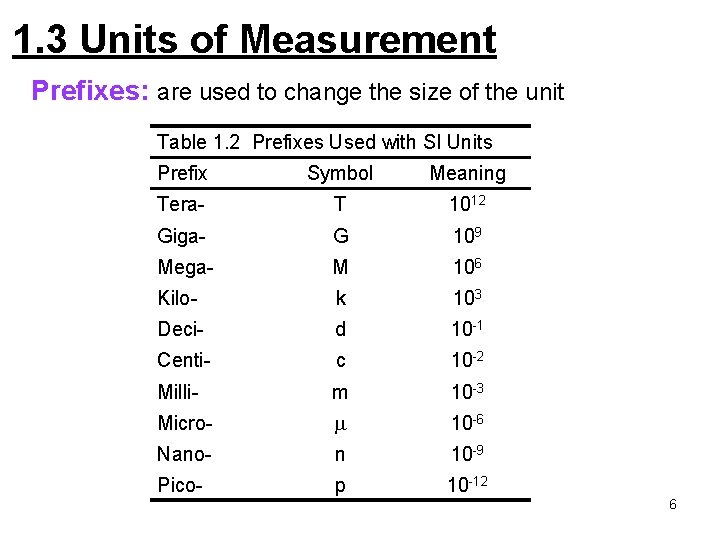
1. 3 Units of Measurement Prefixes: are used to change the size of the unit Table 1. 2 Prefixes Used with SI Units Prefix Symbol Meaning Tera- T 1012 Giga- G 109 Mega- M 106 Kilo- k 103 Deci- d 10 -1 Centi- c 10 -2 Milli- m 10 -3 Micro- m 10 -6 Nano- n 10 -9 Pico- p 10 -12 6

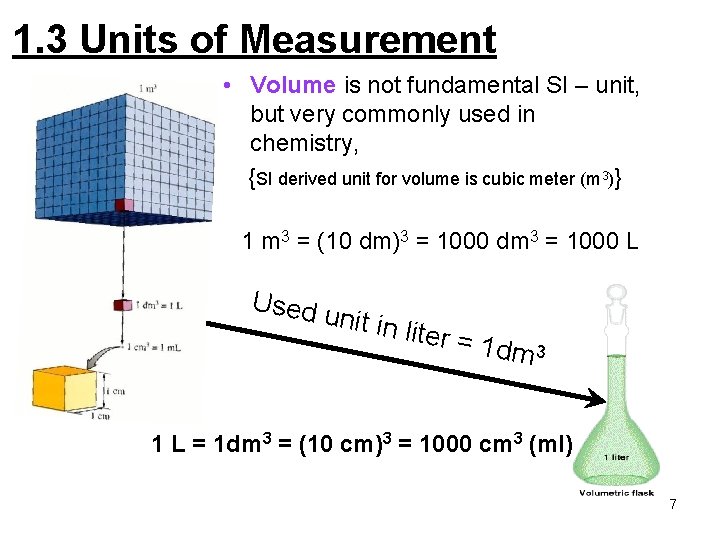
1. 3 Units of Measurement • Volume is not fundamental SI – unit, but very commonly used in chemistry, {SI derived unit for volume is cubic meter (m 3)} 1 m 3 = (10 dm)3 = 1000 dm 3 = 1000 L Used u nit in li ter = 1 dm 3 1 L = 1 dm 3 = (10 cm)3 = 1000 cm 3 (ml) 7

1. 4 Uncertainty in measurement Any measurement always has some degree of uncertainty. Uncertainty depends on the precision of measuring device. e. g. , measurement of volume of a liquid using a buret: • the used liquid is about …………………. m. L If 4 different people read the same volume we might get: Person Result 1 22. 2 2 22. 1 3 22. 3 4 22. 0 8

1. 4 Uncertainty in measurement • You have to record the certain digits and the first uncertain digit only. • All digits together [ certain + first uncertain] are called " Significant Figures" • The uncertainty in the last number must be assumed to be # 1 Volume = 22. 2 ± 0. 1 ml Example 1. 1: What is the difference between the measurements 25. 00 m. L and 25 m. L? 9

1. 4 Uncertainty in measurement Precision and Accuracy • Accuracy: it is the agreement of a particular value with the true value. • Precision: it is the agreement among several measurements of the same quantity. Not Accurate Not precise Not Accurate But precise Accurate and precise 10

1. 4 Uncertainty in measurement Errors • Random error: it means that a measurement has an equal probability of being high or low. • Systematic error: error accurse in the same direction each item. Large Random Error Small Random and Large Systematic Error Small Random And NO Systematic Error 11

1. 5 Significant Figures (SF) and Calculations Rules for Counting Significant Figures: It is important to be applied to get the uncertainty in the final results out of adding, subtracting multiplying. . etc. • Nonzero integers, count as SF. • Zeros: - "Leading zeros” are not significant. e. g. 0. 0025 - "Captive zeros” Count as s. f. e. g. : 1. 008 - "Trailing zeros” count as s. f. eg. : 100 = 1. 00 X 102 (2 SF) (4 SF) (3 SF) • Exact numbers have an infinite number of SF e. g. 10 experiment, 5 apples, 8 books … so on. . . • Exponential notation: it is used to unite large or small numbers in the correct sig. fig. e. g. 0. 000060 convenient 6. 0 x 10 -5 12

1. 5 Significant Figures (SF) and Calculations Rules for SF in Mathematical Operations: • Multiplication / Division: Final results have the same SF in the least precise measurement used in calculation. e. g. 4. 56 x 1. 4 = 6. 38 = (………………? ) • Addition / Subtraction: Final results have the same number of decimal places as the least precise numbers e. g. 12. 11 + 18. 0 + 1. 013 = 31. 123 = (…………? ) 13

1. 5 Significant Figures (SF) and Calculations Note: To get the correct total SF in the final results you may round off the results. Rules for rounding: if the number to be removed is < 5, the preceding digit stays the same. e. g. , round 1. 33 to 2 S. F. (…………? ) Exercise 1. 4: a) 1. 05 x 10 -3 ÷ 6. 135 = (…………. ? ) b) 21 – 13. 8 = (……………? ) 14

1. 6 Dimensional Analysis conversion of a given results from one system unit to an other using "Unit Factor Method" or dimensional analysis. Means Multiply any expression by "1" will not change its value. • Exercise 1. 5: A pencil is 7. 00 in long, What is its length in centimeter? – Solution: • what is the in/cm relation: 2. 54 cm = 1 in • which unit is needed: cm • unit factor must has cm unit as nominator. i. e. 2. 54 cm / 1 in = 1 [unit factor] Multiply the length by the unit factor gives: 7. 00 in x 2. 54 cm /1 in = 17. 8 cm 7. 00 in = 17. 8 cm 15

1. 6 Dimensional Analysis Note: Sometime you have to do multi-step conversion to get correct answer. Exercise 1. 7: A student has entered a 10. 0 km race. How long is the run in miles? • Solution: km m yd mi [1 km = 1000 m, 1 m = 1. 09 yd, 1760 yd = 1 mi] • Results: 10. 0 km = 6. 22 mi 16

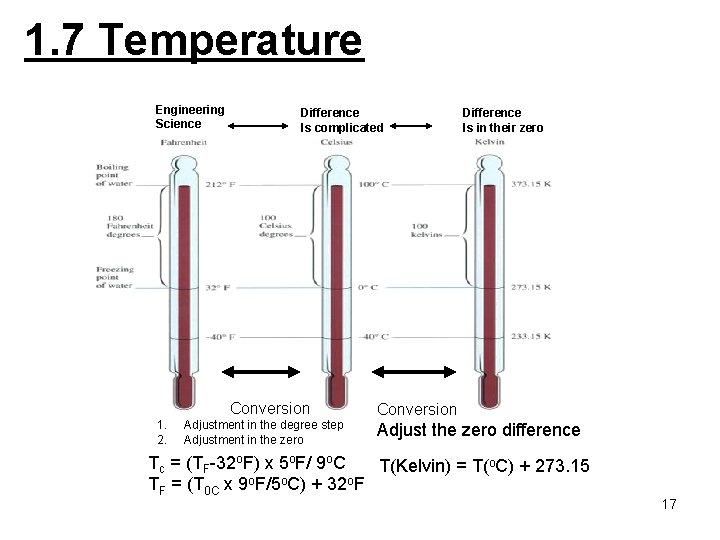
1. 7 Temperature Engineering Science Difference Is complicated Conversion 1. 2. Adjustment in the degree step Adjustment in the zero Difference Is in their zero Conversion Adjust the zero difference Tc = (TF-32 o. F) x 5 o. F/ 9 o. C T(Kelvin) = T(o. C) + 273. 15 TF = (T 0 C x 9 o. F/5 o. C) + 32 o. F 17

1. 8 Density It is the mass per unit volume of the substance. A property of matter that is often used by chemists. Density = Exercise 1. 13: A chemist finds that 25. 00 cm 3 of a CD- cleaner has a mass of 19. 625 g at 20 o. C. The following are the names and densities of the compounds that might be the main component: Which of them is the most likely to be the main component of the CD-cleaner? Solution: Chloroform 1. 492 g / cm 3 At 20 o. C Diethyl ether 0. 714 g / cm 3 At 20 o. C Ethanol 0. 789 g / cm 3 At 20 o. C Isopropyl alcohol 0. 785 g / cm 3 At 20 o. C Toluene 0. 867 g / cm 3 At 20 o. C 18

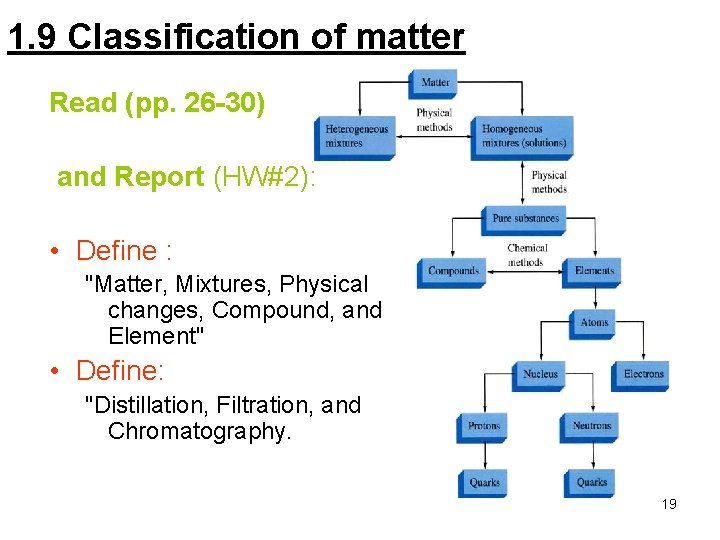
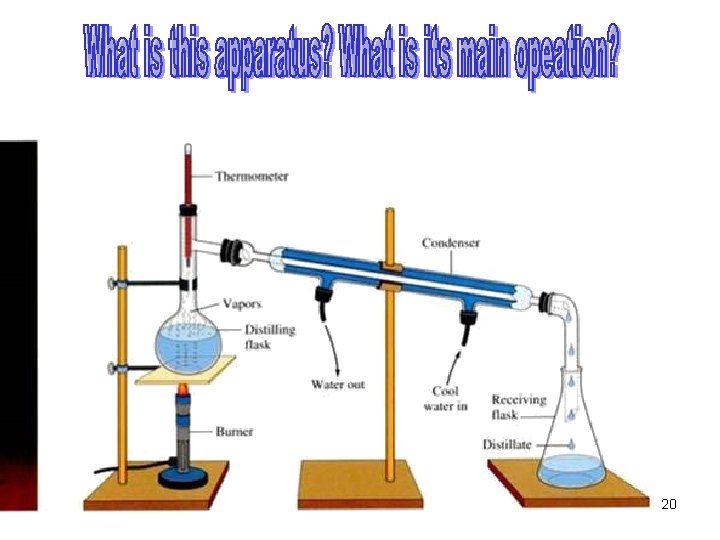
1. 9 Classification of matter Read (pp. 26 -30) and Report (HW#2): • Define : "Matter, Mixtures, Physical changes, Compound, and Element" • Define: "Distillation, Filtration, and Chromatography. 19

20