CHE20028 PHYSICAL INORGANIC CHEMISTRY QUANTUM CHEMISTRY LECTURE 3

CHE-20028: PHYSICAL & INORGANIC CHEMISTRY QUANTUM CHEMISTRY: LECTURE 3 Dr Rob Jackson Office: LJ 1. 16 r. a. jackson@keele. ac. uk http: //www. facebook. com/robjteaching

Use of the Schrödinger Equation in Chemistry • The Schrödinger equation introduced • What it means and what it does • Applications: – The particle in a box – The harmonic oscillator – The hydrogen atom CHE-20028 QC lecture 3 2

Learning objectives for lecture 3 • What the terms in the equation represent and what they do. • How the equation is applied to two general examples (particle in a box, harmonic oscillator) and one specific example (the hydrogen atom). CHE-20028 QC lecture 3 3

The Schrödinger Equation introduced • The equation relates the wave function to the energy of any ‘system’ (general system or specific atom or molecule). • In the last lecture we introduced the wave function, , and defined it as a function which contains all the available information about what it is describing, e. g. a 1 s electron in hydrogen. CHE-20028 QC lecture 3 4

What does the equation do? • It uses mathematical techniques to ‘operate’ on the wave function to give the energy of the system being studied, using mathematical functions called ‘operators’. • The energy is divided into potential and kinetic energy terms. CHE-20028 QC lecture 3 5

The equation itself • The simplest way to write the equation is: H = E • This means ‘an operator, H, acts on the wave function to give the energy E’. – Note – don’t read it like a normal algebraic equation! CHE-20028 QC lecture 3 6

More about the operator H Remember, energy is divided into potential and kinetic forms. H is called the Hamiltonian operator (after the Irish mathematician Hamilton). The Hamiltonian operator contains 2 terms, which are connected respectively with the kinetic and potential energies. William Rowan Hamilton (1805– 1865) CHE-20028 QC lecture 3 7

Obtaining the energy • So when H operates on the wave function we obtain the potential and kinetic energies of whatever is being described – e. g. a 1 s electron in hydrogen. • The PE will be associated with the attraction of the nucleus, and the KE with ‘movement’ of the electron. CHE-20028 QC lecture 3 8

What does H look like? • We can write H as: H = T + V, where ‘T’ is the kinetic energy operator, and ‘V’ is the potential energy operator. • The potential energy operator will depend on the system, but the kinetic energy operator has a common form: CHE-20028 QC lecture 3 9

The kinetic energy operator • The operator looks like: • Which means: differentiate the wave function twice and multiply by • means ‘h divided by 2 ’ and m is, e. g. , the mass of the electron CHE-20028 QC lecture 3 10

Examples • Use of the Schrödinger equation is best illustrated through examples. • There are two types of example, generalised ones and specific ones, and we will consider three of these. • In each case we will work out the form of the Hamiltonian operator. CHE-20028 QC lecture 3 11

Particle in a box • The simplest example, a particle moving between 2 fixed walls: A particle in a box is free to move in a space surrounded by impenetrable barriers (red). When the barriers lie very close together, quantum effects are observed. CHE-20028 QC lecture 3 12

Particle in a box: relevance • 2 examples from Physics & Chemistry: • Semiconductor quantum wells, e. g. Ga. As between two layers of Alx. Ga 1 -x. As • electrons in conjugated molecules, e. g. butadiene, CH 2=CH-CH=CH 2 • References for more information will be given on the teaching pages. CHE-20028 QC lecture 3 13

Particle in a box – (i) • The derivation will be explained in the lecture, but the key equations are: (i) possible wavelengths are given by: = 2 L/n (L is length of the box), n = 1, 2, 3. . . See http: //www. chem. uci. edu/undergrad/applets/dwell. htm (ii) p = h/ = nh/2 L (from de Broglie equation) CHE-20028 QC lecture 3 14

Particle in a box – (ii) • (iii) the kinetic energy is related to p (momentum) by E = p 2/2 m • Permitted energies are therefore: En = n 2 h 2/8 m. L 2 (with n = 1, 2, 3. . . ) • So the particle is shown to only be able to have certain energies – this is an example of quantisation of energy. CHE-20028 QC lecture 3 15

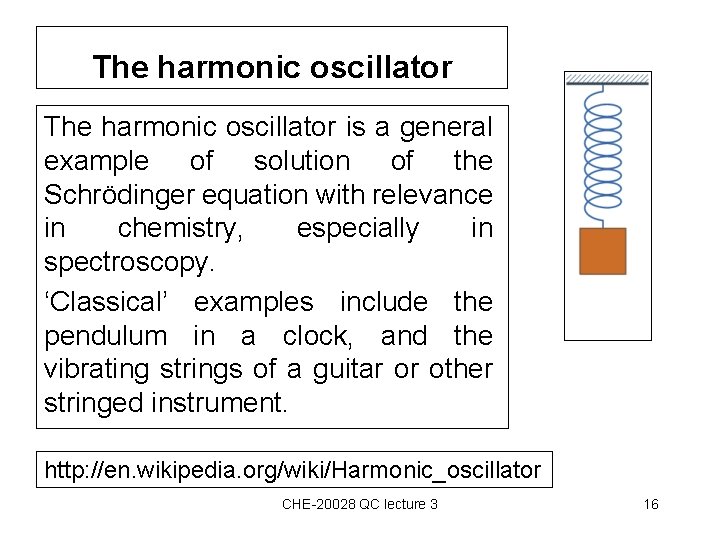
The harmonic oscillator is a general example of solution of the Schrödinger equation with relevance in chemistry, especially in spectroscopy. ‘Classical’ examples include the pendulum in a clock, and the vibrating strings of a guitar or other stringed instrument. http: //en. wikipedia. org/wiki/Harmonic_oscillator CHE-20028 QC lecture 3 16

Example of a harmonic oscillator: a diatomic molecule H ------ H • If one of the atoms is displaced from its equilibrium position, it will experience a restoring force F, proportional to the displacement. F = - kx • where x is the displacement, and k is a force constant. • Note negative sign: force is in the opposite direction to the displacement CHE-20028 QC lecture 3 17

Restoring force and potential energy • And by integration, we can get the potential energy: • So we can write the Hamiltonian for the harmonic oscillator: • V(x) = k x dx • =½ kx 2 • H= CHE-20028 QC lecture 3 18

1 -dimensional harmonic oscillator summarised F = - kx • where x is the displacement, and k is a force constant. • Note negative sign: force is in the opposite direction to the displacement • And by integration, we can get the potential energy: • V(x) = k x dx • = ½ kx 2 • So we can write the Hamiltonian for the harmonic oscillator: • H= CHE-20028 QC lecture 3 19

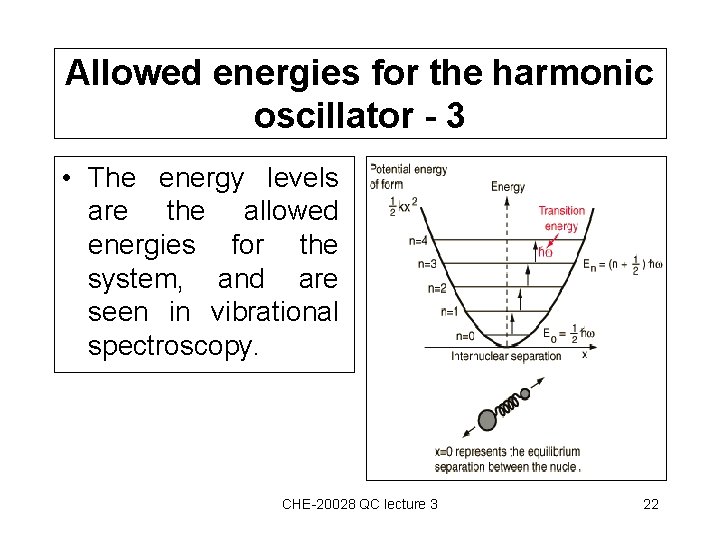
Allowed energies for the harmonic oscillator - 1 • If we have an expression for the wave function of a harmonic oscillator (outside module scope!), we can use Schrödinger’s equation to get the energy. • It can be shown that only certain energy levels are allowed – this is a further example of energy quantisation. CHE-20028 QC lecture 3 20

Allowed energies for the harmonic oscillator - 2 En = (n+½) • is the circular frequency, and n= 0, 1, 2, 3, 4 • An important result is that when n=0, E 0 is not zero, but ½ . • This is the zero point energy, and this occurs in quantum systems but not classically – a pendulum can be at rest! CHE-20028 QC lecture 3 21

Allowed energies for the harmonic oscillator - 3 • The energy levels are the allowed energies for the system, and are seen in vibrational spectroscopy. CHE-20028 QC lecture 3 22

Quantum and classical behaviour • Quantum behaviour (atomic systems) characterised by zero point energy, and quantisation of energy. • Classical behaviour (pendulum, swings etc) – systems can be at rest, and can accept energy continuously. • We now look at a specific chemical system and apply the same principles. CHE-20028 QC lecture 3 23

The hydrogen atom • Contains 1 proton and 1 electron. • So there will be: – potential energy of attraction between the electron and the proton – kinetic energy of the electron • (we ignore kinetic energy of the proton Born-Oppenheimer approximation). CHE-20028 QC lecture 3 24

The Hamiltonian operator for hydrogen - 1 • H will have 2 terms, for the electron kinetic energy and the proton-electron potential energy H = Te + Vne • Writing the terms in full, the most straightforward is Vne : Vne = -e 2/4 0 r (Coulomb’s Law) • Note negative sign - attraction CHE-20028 QC lecture 3 25

The Hamiltonian operator for hydrogen - 2 • The kinetic energy operator will be as before but in 3 dimensions: • A shorthand version of the term in brackets is 2. • We can now re-write Te and the full expression for H. CHE-20028 QC lecture 3 26

The Hamiltonian operator for hydrogen – 3 H = Te + Vne • So, in full: H = (-ħ 2/2 m) 2 -e 2/4 0 r • The Schrödinger equation for the H atom is therefore: {(-ħ 2/2 m) 2 -e 2/4 0 r} = E CHE-20028 QC lecture 3 27

Hamiltonians for molecules • When there are more nuclei and electrons the expressions for H get longer. • H 2+ and H 2 will be written as examples. • Note that H 2 has an electron repulsion term: +e 2/4 0 r CHE-20028 QC lecture 3 28

Energies and orbitals • Solve Schrödinger’s equation using the Hamiltonian, and an expression for the wavefunction, : En = -RH/n 2 (n=1, 2, 3 …) (RH: Rydberg’s constant) • The expression for the wavefunction is: (r, , ) = R(r) Y( , ) • s-functions don’t depend on the angular part, Y( , ); only depend on R(r). CHE-20028 QC lecture 3 29

Conclusions on lecture • The Schrödinger equation has been introduced (and the Hamiltonian operator defined), and applied to: – The particle in a box – The harmonic oscillator – The hydrogen atom • In all cases, the allowed energies are found to be quantised. CHE-20028 QC lecture 3 30

Final conclusions from the Quantum Chemistry lectures • Two important concepts have been introduced: wave-particle duality, and quantisation of energy. • In each case, experiments and examples have been given to illustrate the development of the concepts. CHE-20028 QC lecture 3 31