CHE 402 Kinetics and Reactor Design CHAPTER TWO

CHE 402: Kinetics and Reactor Design CHAPTER TWO Conversion and Reactor Sizing Mustafa Nasser, Ph. D, MSc, BSc Chemical Engineering Dr Mustafa Nasser 2012 1

Reaction Conversion �Consider �on the general reaction; a “per mole of A basis”… Dr Mustafa Nasser 2012 2

Reaction Conversion �The conversion of A (XA) is defined as: Dr Mustafa Nasser 2012 3

Conversion (Batch System) �Consider the batch reactor mole balance: Dr Mustafa Nasser 2012 4

Batch Reactor Design Equation �Recall the batch reactor design equation differential form integral form Dr Mustafa Nasser 2012 5

Conversion (Flow System) �Consider the flow reactor mole balance: Dr Mustafa Nasser 2012 6

CSTR Design Equations �Recall the CSTR Design Equation: Dr Mustafa Nasser 2012 7

PFR Design Equations �Recall the PFR Design Equation: differential form integral form Dr Mustafa Nasser 2012 8

Application of Design Equations �Consider a single reaction system with functional dependence as; Dr Mustafa Nasser 2012 9

Application of Design Equations: Levenspiel Plots Dr Mustafa Nasser 2012 10

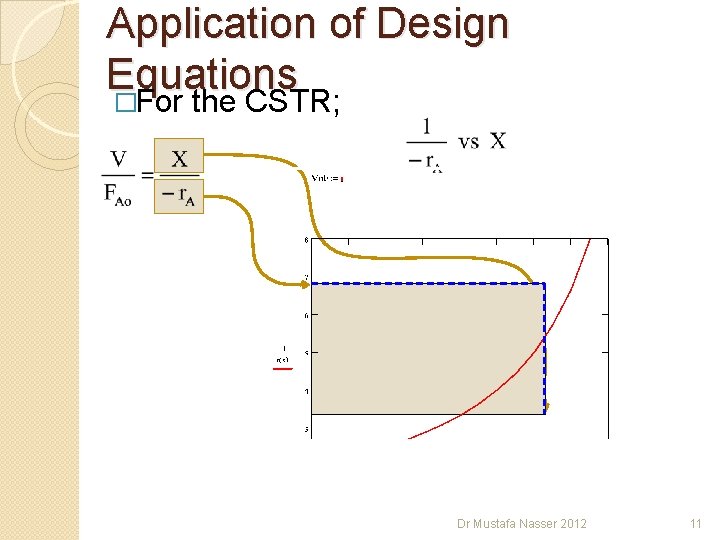
Application of Design Equations �For the CSTR; Dr Mustafa Nasser 2012 11

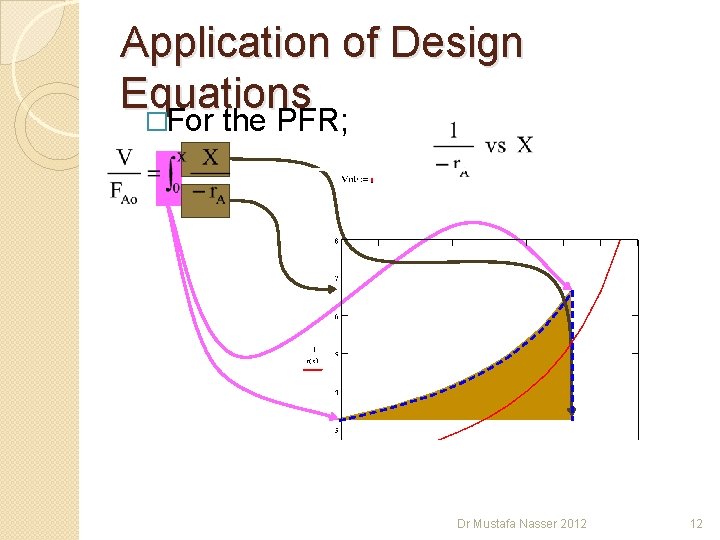
Application of Design Equations �For the PFR; Dr Mustafa Nasser 2012 12

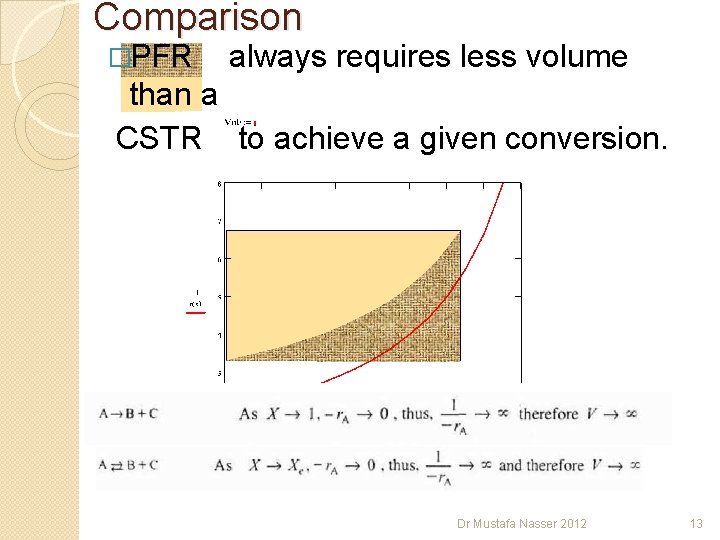
Comparison �PFR always requires less volume than a CSTR to achieve a given conversion. Dr Mustafa Nasser 2012 13

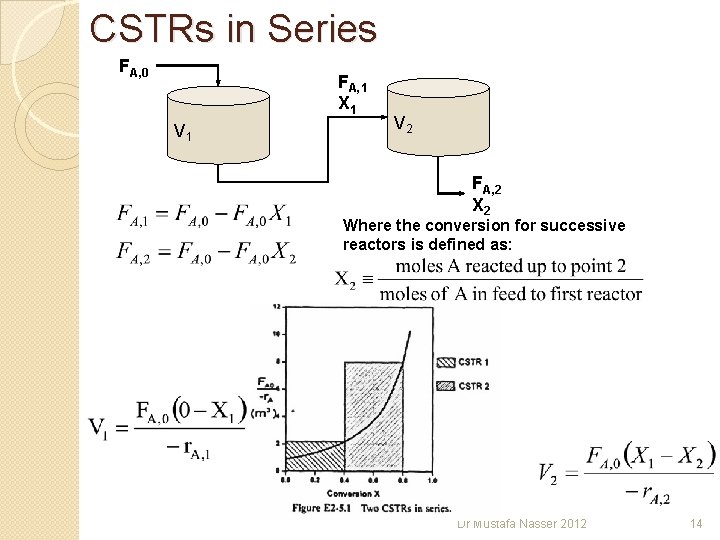
CSTRs in Series FA, 0 FA, 1 X 1 V 2 FA, 2 X 2 Where the conversion for successive reactors is defined as: Dr Mustafa Nasser 2012 14

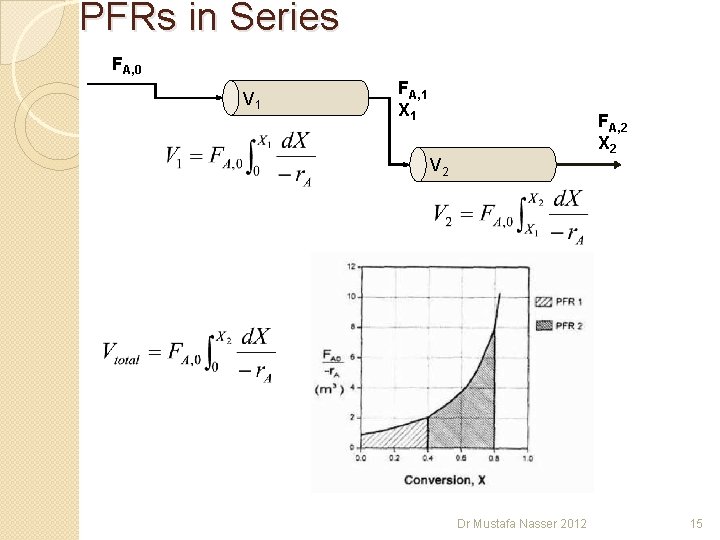
PFRs in Series FA, 0 V 1 FA, 1 X 1 FA, 2 X 2 V 2 Dr Mustafa Nasser 2012 15

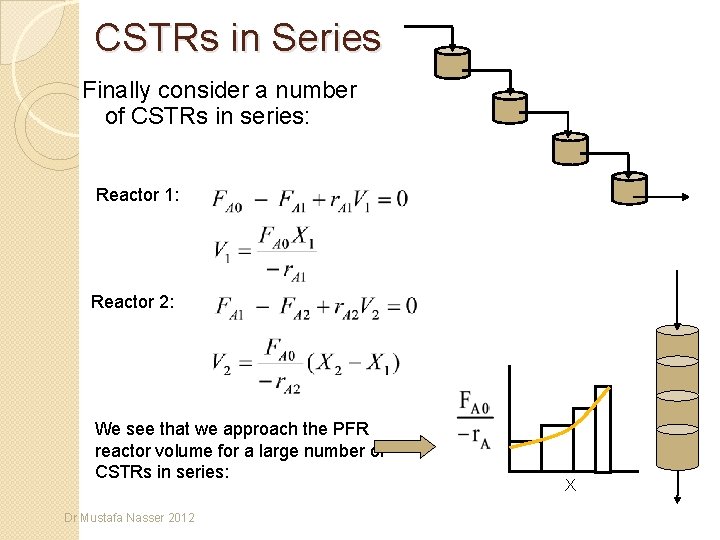
CSTRs in Series Finally consider a number of CSTRs in series: Reactor 1: Reactor 2: We see that we approach the PFR reactor volume for a large number of CSTRs in series: Dr Mustafa Nasser 2012 X

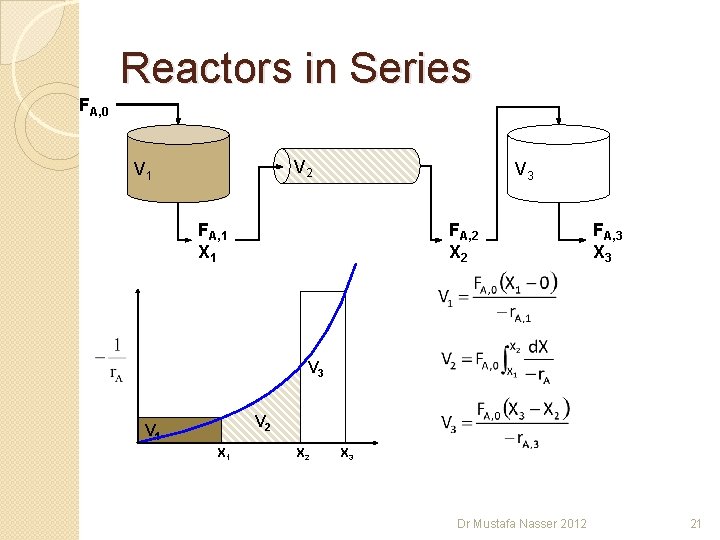
Reactors in Series FA, 0 V 2 V 1 FA, 1 X 1 V 3 FA, 2 X 2 FA, 3 X 3 Where the conversion for successive reactors is defined as: Dr Mustafa Nasser 2012 17

Reactors in Series FA, 0 V 2 V 1 FA, 1 X 1 V 3 FA, 2 X 2 Dr Mustafa Nasser 2012 FA, 3 X 3 18

Reactors in Series FA, 0 V 2 V 1 FA, 1 X 1 V 3 FA, 2 X 2 Dr Mustafa Nasser 2012 FA, 3 X 3 19

Reactors in Series FA, 0 V 2 V 1 FA, 1 X 1 V 3 FA, 2 X 2 Dr Mustafa Nasser 2012 FA, 3 X 3 20

Reactors in Series FA, 0 V 2 V 1 V 3 FA, 1 X 1 FA, 2 X 2 FA, 3 X 3 V 2 V 1 X 2 X 3 Dr Mustafa Nasser 2012 21

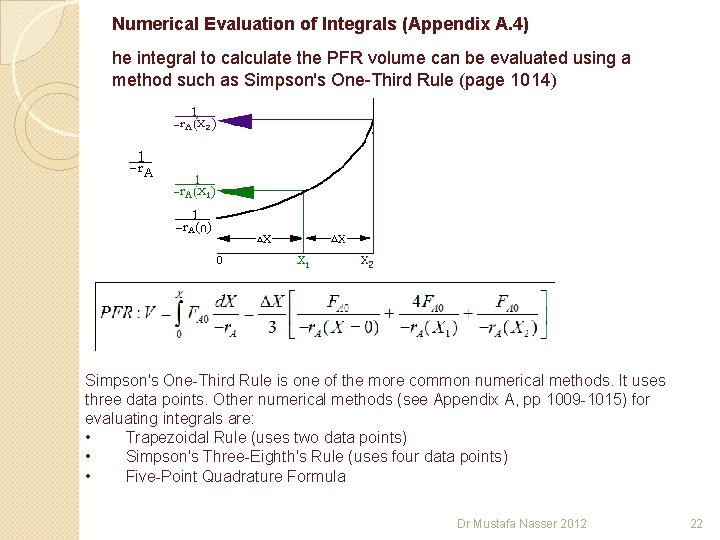
Numerical Evaluation of Integrals (Appendix A. 4) he integral to calculate the PFR volume can be evaluated using a method such as Simpson's One-Third Rule (page 1014) Simpson's One-Third Rule is one of the more common numerical methods. It uses three data points. Other numerical methods (see Appendix A, pp 1009 -1015) for evaluating integrals are: • Trapezoidal Rule (uses two data points) • Simpson's Three-Eighth's Rule (uses four data points) • Five-Point Quadrature Formula Dr Mustafa Nasser 2012 22

Relative Reaction Rates �Relative reaction rates of the species involved in a reaction can be obtained from the stoichiometric coefficients: Dr Mustafa Nasser 2012 23

Space Time ( ) �Time necessary to process 1 reactor volume of fluid at entrance conditions ◦ Also called residence time or holding time ◦ 1/ is referred to as the Space Velocity ◦ For a PFR, Dr Mustafa Nasser 2012 24

Dr Mustafa Nasser 2012 25

Dr Mustafa Nasser 2012 26

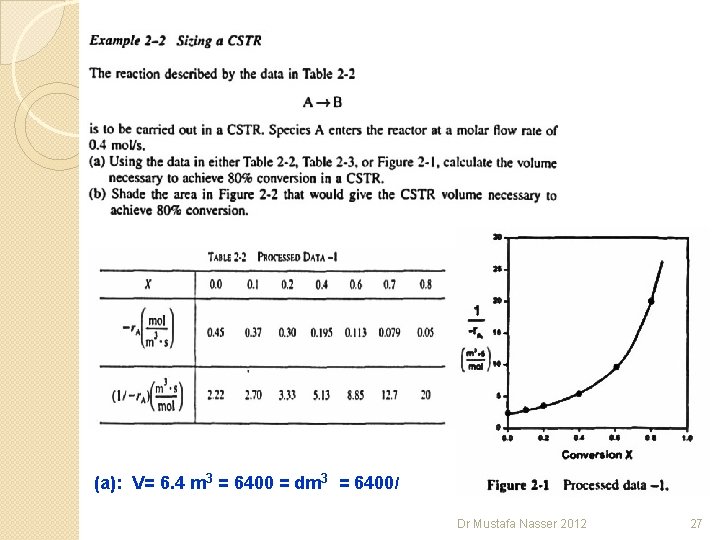
(a): V= 6. 4 m 3 = 6400 = dm 3 = 6400 l Dr Mustafa Nasser 2012 27

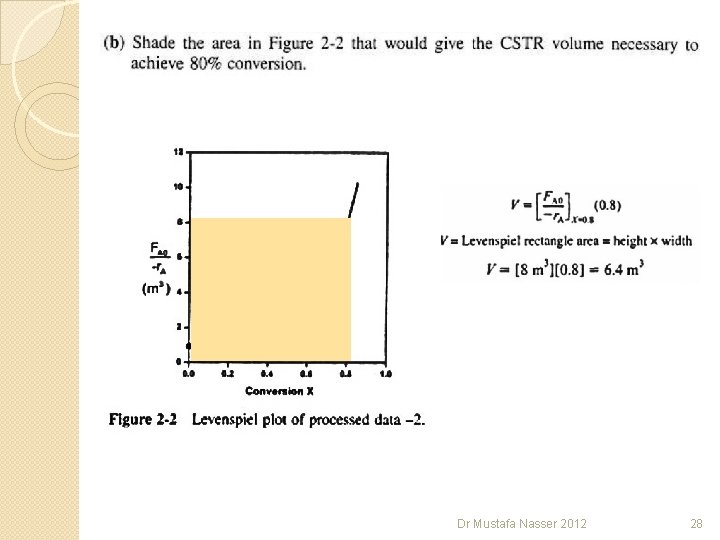
Dr Mustafa Nasser 2012 28

Dr Mustafa Nasser 2012 29

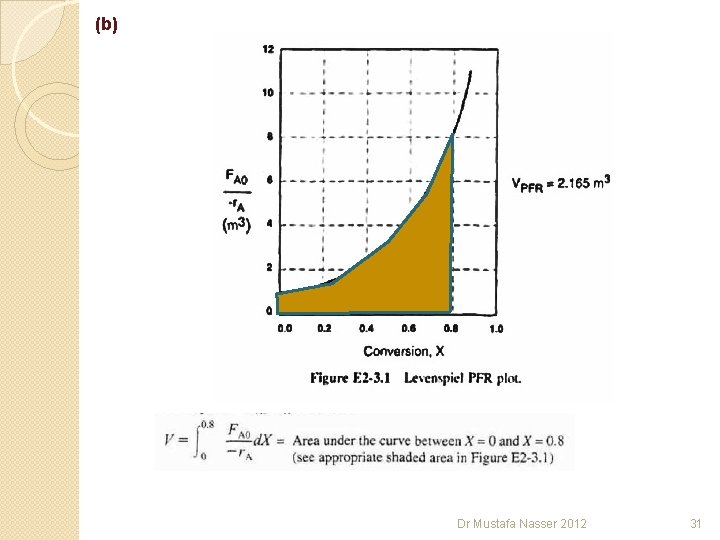
(a) Dr Mustafa Nasser 2012 30

(b) Dr Mustafa Nasser 2012 31

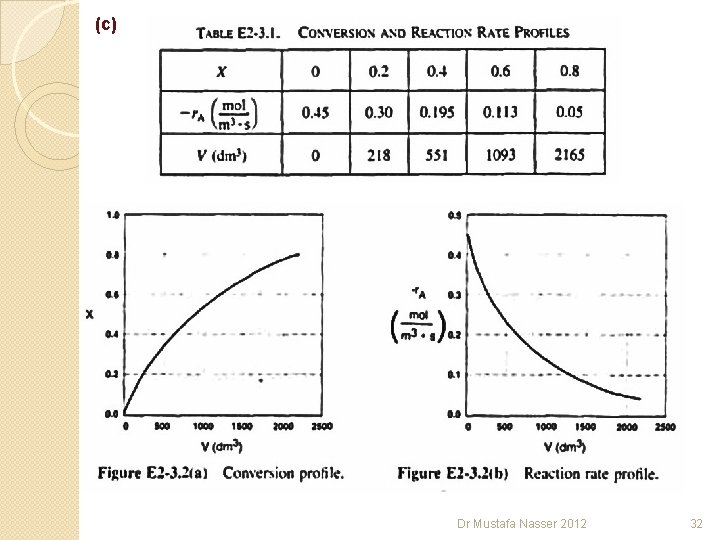
(c) Dr Mustafa Nasser 2012 32

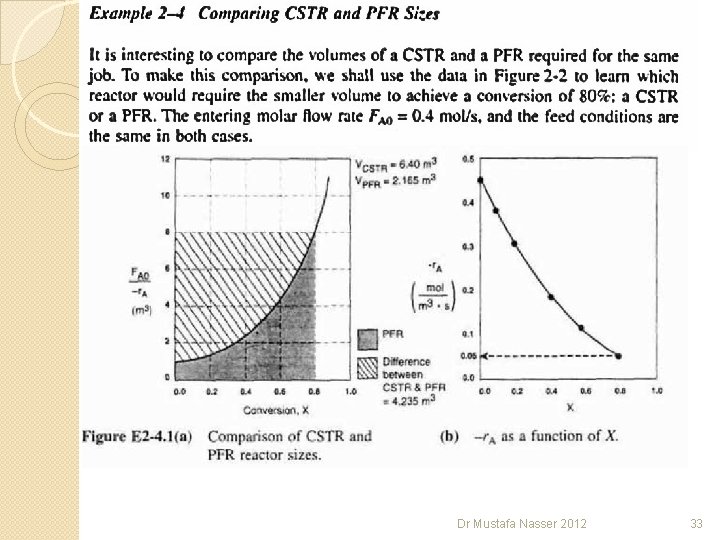
Dr Mustafa Nasser 2012 33

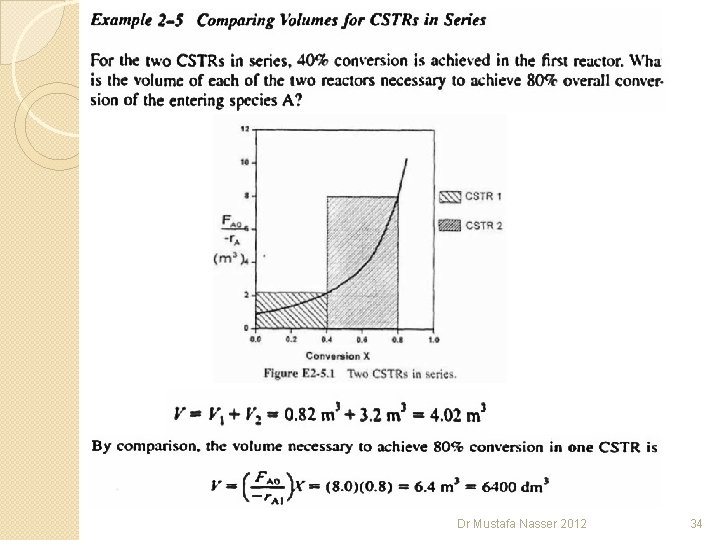
Dr Mustafa Nasser 2012 34

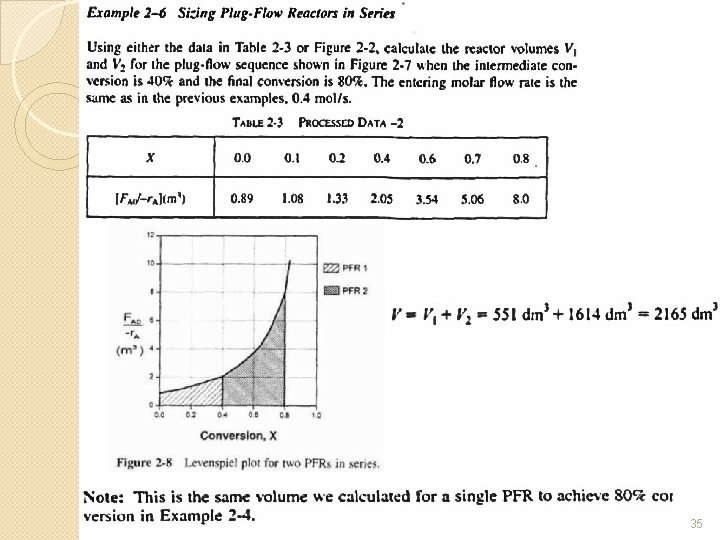
Dr Mustafa Nasser 2012 35

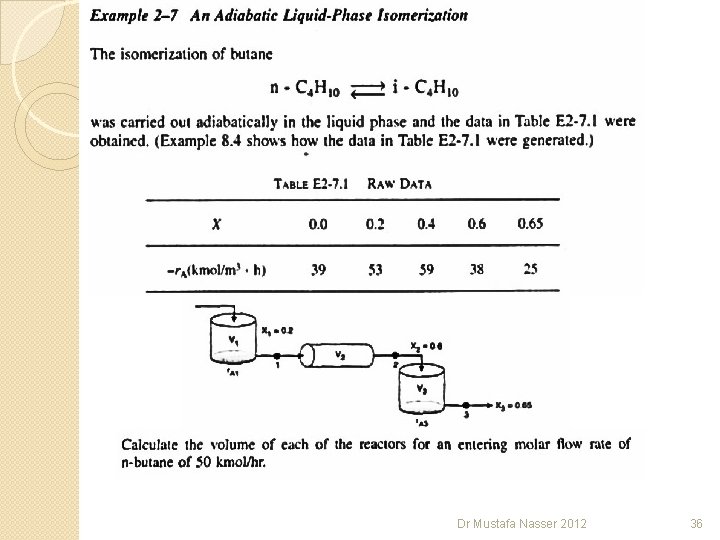
Dr Mustafa Nasser 2012 36

Solution 2 -7 Dr Mustafa Nasser 2012 37

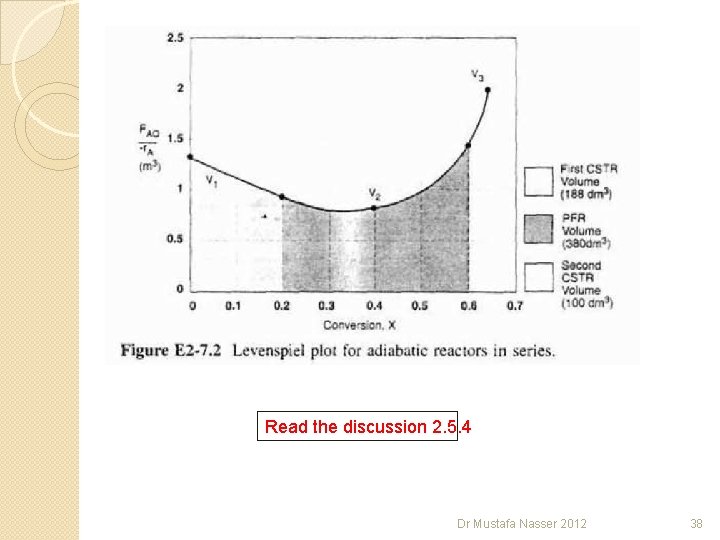
Read the discussion 2. 5. 4 Dr Mustafa Nasser 2012 38

Try This: Dr Mustafa Nasser 2012 39