Chase Methods based on Knowledge Discovery Agnieszka Dardzinska

Chase Methods based on Knowledge Discovery Agnieszka Dardzinska & Zbigniew W. Ras agnadar@wp. pl & ras@uncc. edu
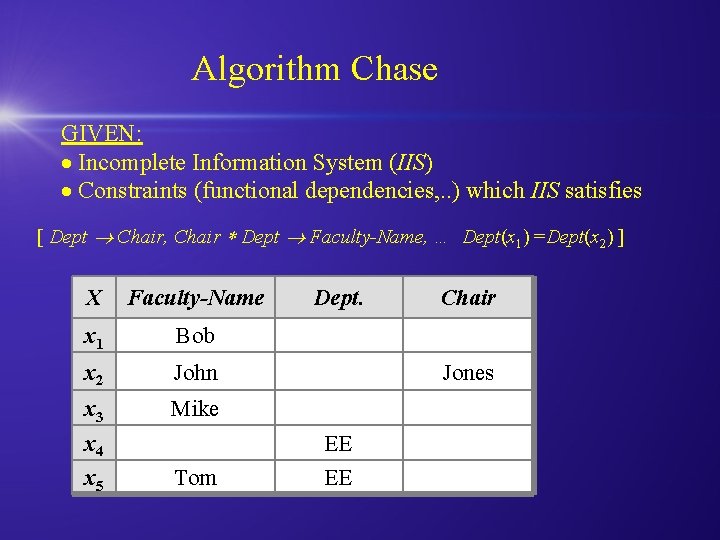
Algorithm Chase GIVEN: Incomplete Information System (IIS) Constraints (functional dependencies, . . ) which IIS satisfies [ Dept Chair, Chair Dept Faculty-Name, … Dept(x 1) =Dept(x 2) ] X Faculty-Name x 1 Bob x 2 John x 3 Mike x 4 x 5 Dept. Jones EE Tom Chair EE
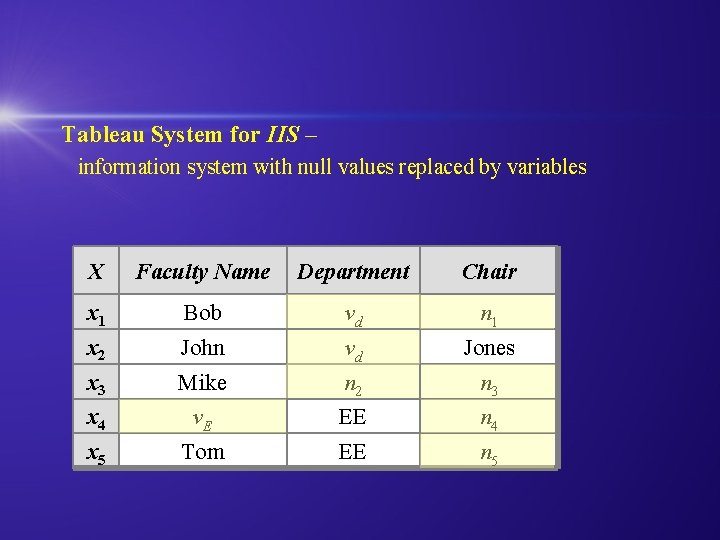
Tableau System for IIS – information system with null values replaced by variables X Faculty Name Department Chair x 1 Bob vd n 1 x 2 John vd Jones x 3 Mike n 2 n 3 x 4 v. E EE n 4 x 5 Tom EE n 5

Variables in Tableaux System q distinguished variables, one for each attribute (if b is an attribute of interest, then vb is the corresponding distinguished variable) q nondistinguished variables (there are countably many of them: n 1, n 2, n 3, …. )
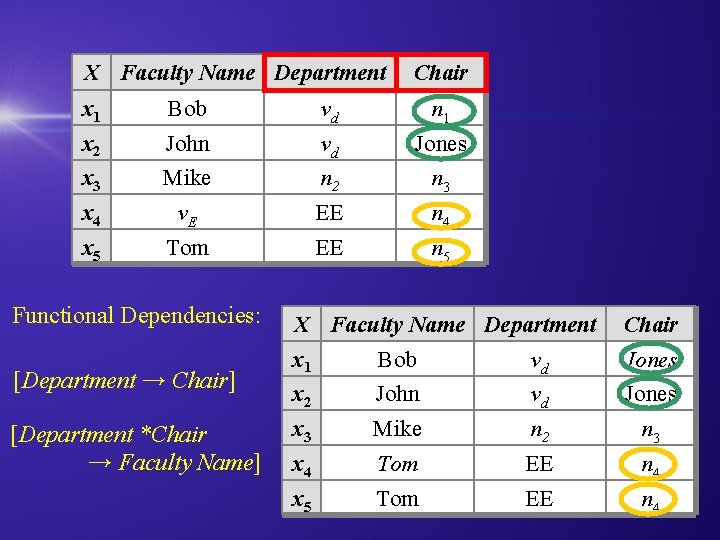
X Faculty Name Department Chair x 1 Bob vd n 1 x 2 John vd Jones x 3 Mike n 2 n 3 x 4 v. E EE n 4 x 5 Tom EE n 5 Functional Dependencies: [Department → Chair] [Department *Chair → Faculty Name] X Faculty Name Department Chair x 1 Bob vd Jones x 2 John vd Jones x 3 Mike n 2 n 3 x 4 Tom EE n 4 x 5 Tom EE n 4

Algorithm Chase Input: tableaux system S and set of functional dependencies F Output: tableaux system CHASEF(S) Begin S 1: =S; while there are t 1, t 2 S 1 and (B b) F such that t 1[B]= t 2[B] and t 1[b] < t 2[b] do change all the occurrences of the value t 2[b] in S 1 to t 1[b] CHASEF(S): =S 1 End

Algorithm Chase Input: tableaux system S and set of functional dependencies F Output: tableaux system CHASEF(S) Begin S 1: =S; while there are t 1, t 2 S 1 and (B b) F such that t 1[B]= t 2[B] and t 1[b] < t 2[b] do change all the occurrences of the value t 2[b] in S 1 to t 1[b] CHASEF(S): =S 1 End The algorithm always terminates if applied to a finite tableaux system. If one execution of the algorithm generates a tableaux system satisfying F, then every execution of the algorithm generates the same tableaux system.

Algorithm Chase 1

Chase supported by rules extracted from IIS (Chase 1) 1. Chase 1 identifies all incomplete attributes (their values are called concepts) in IS. 2. Main Algorithm - Extraction of rules from IS describing these concepts, - Null values in IS are replaced by values suggested by these rules. 3. These two steps are repeated till fixpoint is reached.

Example (Chase 1) X b c d x 1 b 1 c 1 e f e 2 f 1 g X = {x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8, x 9, x 10} x 2 b 2 c 2 d 2 e 1 f 2 g 3 x 3 b 1 c 1 d 3 e 1 f 1 g 1 A = {b, c, d, e, f, g} x 4 b 3 c 3 d 3 e 3 f 1 g 2 f 2 g 1 Attribute b e 2 b 1 c 1 f 1 b 1 g 2 b 2 c 3 b 3 c 2 b 2 g 3 d 2 b 2 e 3 d 3 b 3 f 2 d 2 b 2 x 5 b 2 c 2 x 6 c 1 d 2 x 7 b 1 d 2 e 2 f 4 g 1 x 8 d 2 e 2 f 2 g 3 x 9 b 3 c 1 d 1 x 10 b 2 c 1 f 2 e 3 f 4 g 2 (support 2), (support 1), (support 1).

Example (Chase 1) X b c d x 1 b 1 c 1 e f e 2 f 1 g x 2 b 2 c 2 d 2 e 1 f 2 g 3 x 3 b 1 c 1 d 3 e 1 f 1 g 1 x 4 b 3 c 3 d 3 e 3 f 1 g 2 f 2 g 1 x 5 b 2 c 2 x 6 c 1 d 2 x 7 b 1 d 2 e 2 f 4 g 1 x 8 d 2 e 2 f 2 g 3 x 9 b 3 c 1 d 1 x 10 b 2 c 1 f 2 e 3 f 4 g 2 Attribute b Two null values in S: b(x 6), b(x 8) b(x 6): e 2 b 1 c 1 f 1 b 1 g 2 b 2 c 3 b 3 c 2 b 2 g 3 d 2 b 2 e 3 d 3 b 3 f 2 d 2 b 2 (support 2), (support 1), (support 1).

Example (Chase 1) X b c d x 1 b 1 c 1 e f e 2 f 1 g x 2 b 2 c 2 d 2 e 1 f 2 g 3 x 3 b 1 c 1 d 3 e 1 f 1 g 1 x 4 b 3 c 3 d 3 e 3 f 1 g 2 f 2 g 1 x 5 b 2 c 2 x 6 c 1 d 2 x 7 b 1 d 2 e 2 f 4 g 1 x 8 d 2 e 2 f 2 g 3 x 9 b 3 c 1 d 1 x 10 b 2 c 1 f 2 e 3 f 4 g 2 Attribute b Two null values in S: b(x 6), b(x 8) b(x 6): e 2 b 1 c 1 f 1 b 1 g 2 b 2 c 3 b 3 c 2 b 2 g 3 d 2 b 2 e 3 d 3 b 3 f 2 d 2 b 2 (support 2), (support 1), (support 1).

Example (Chase 1) X b c d x 1 b 1 c 1 e f e 2 f 1 g x 2 b 2 c 2 d 2 e 1 f 2 g 3 x 3 b 1 c 1 d 3 e 1 f 1 g 1 x 4 b 3 c 3 d 3 e 3 f 1 g 2 f 2 g 1 x 5 b 2 c 2 x 6 c 1 d 2 x 7 b 1 d 2 e 2 f 4 g 1 x 8 d 2 e 2 f 2 g 3 x 9 b 3 c 1 d 1 x 10 b 2 c 1 b(x 6) = b 2 f 2 e 3 f 4 g 2 Attribute b Two null values in S: b(x 6), b(x 8): e 2 b 1 c 1 f 1 b 1 g 2 b 2 c 3 b 3 c 2 b 2 g 3 d 2 b 2 e 3 d 3 b 3 f 2 d 2 b 2 (support 2), (support 1), (support 1).

Example (Chase 1) X b c d x 1 b 1 c 1 e f e 2 f 1 g x 2 b 2 c 2 d 2 e 1 f 2 g 3 x 3 b 1 c 1 d 3 e 1 f 1 g 1 x 4 b 3 c 3 d 3 e 3 f 1 g 2 f 2 g 1 x 5 b 2 c 2 x 6 c 1 d 2 x 7 b 1 d 2 e 2 f 4 g 1 x 8 d 2 e 2 f 2 g 3 x 9 b 3 c 1 d 1 x 10 b 2 c 1 b(x 6) = b 2 f 2 e 3 f 4 g 2 Two null values in S: c(x 7), c(x 8). c(x 7): b 1 c 1 e 2 c 1 f 4 c 1 g 1 c 1 b 2 d 2 c 2 b 2 e 1 c 2 b 2 f 2 c 2 b 2 g 3 c 2 d 2 e 1 c 2 d 2 g 3 c 2 (support 2), (support 1), (support 1), (support 1).
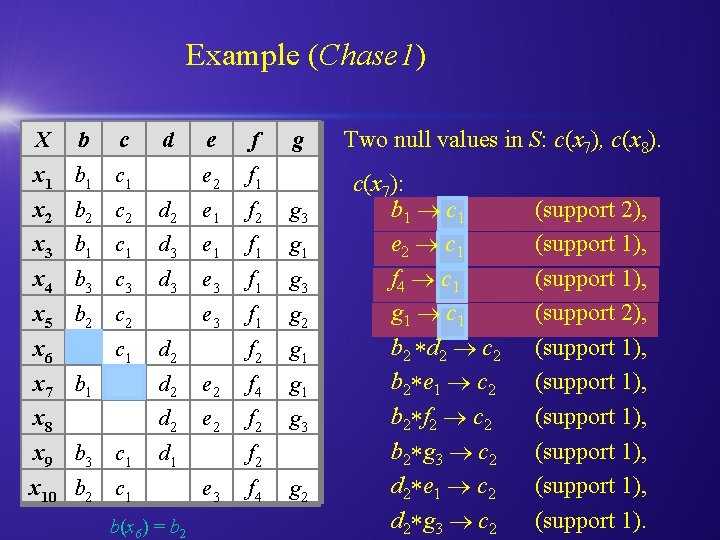
Example (Chase 1) X b c d x 1 b 1 c 1 e f e 2 f 1 g x 2 b 2 c 2 d 2 e 1 f 2 g 3 x 3 b 1 c 1 d 3 e 1 f 1 g 1 x 4 b 3 c 3 d 3 e 3 f 1 g 2 f 2 g 1 x 5 b 2 c 2 x 6 c 1 d 2 x 7 b 1 d 2 e 2 f 4 g 1 x 8 d 2 e 2 f 2 g 3 x 9 b 3 c 1 d 1 x 10 b 2 c 1 b(x 6) = b 2 f 2 e 3 f 4 g 2 Two null values in S: c(x 7), c(x 8). c(x 7): b 1 c 1 e 2 c 1 f 4 c 1 g 1 c 1 b 2 d 2 c 2 b 2 e 1 c 2 b 2 f 2 c 2 b 2 g 3 c 2 d 2 e 1 c 2 d 2 g 3 c 2 (support 2), (support 1), (support 1), (support 1).

Example (Chase 1) X b c d x 1 b 1 c 1 e f e 2 f 1 g x 2 b 2 c 2 d 2 e 1 f 2 g 3 x 3 b 1 c 1 d 3 e 1 f 1 g 1 x 4 b 3 c 3 d 3 e 3 f 1 g 2 f 2 g 1 x 5 b 2 c 2 x 6 c 1 d 2 x 7 b 1 d 2 e 2 f 4 g 1 x 8 d 2 e 2 f 2 g 3 x 9 b 3 c 1 d 1 x 10 b 2 c 1 b(x 6) = b 2 , f 2 e 3 f 4 c(x 7) = c 1 g 2 Two null values in S: c(x 7), c(x 8): b 1 c 1 e 2 c 1 f 4 c 1 g 1 c 1 b 2 d 2 c 2 b 2 e 1 c 2 b 2 f 2 c 2 b 2 g 3 c 2 d 2 e 1 c 2 d 2 g 3 c 2 (support 2), (support 1), (support 1), (support 1).

Algorithm Chase 1(S, In(A), L(D)) Input: System S=(X, A, V) Set of incomplete attributes In(A)={a 1, a 2, …, ak} Set of rules L(D) Output: System Chase 1(S) begin j: =1; while j ≤ k do begin Sj: =S for all v Vaj do while there is x X and rule (t v) L(D) such that x NSj(t) and card(aj(x))≠ 1 begin a(x): =v; end j: =j+1 end S: = {Sj: 1 ≤ j ≤ k}, Chase 1 (S, In(A), L(D)) end
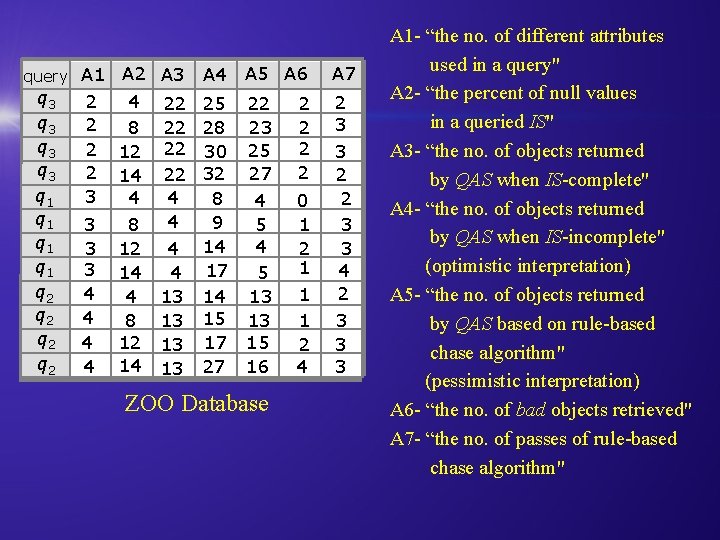
query A 1 q 3 q 3 q 1 q 1 q 2 q 2 2 2 3 3 4 4 A 2 A 3 4 22 8 22 12 22 14 22 4 4 4 8 12 4 14 4 4 13 8 13 12 13 14 13 A 4 A 5 A 6 25 22 28 23 30 25 32 27 8 4 9 5 14 4 17 5 14 13 15 13 17 15 27 16 ZOO Database 2 2 0 1 2 1 1 1 2 4 A 7 2 3 3 2 2 3 3 4 2 3 3 3 A 1 - “the no. of different attributes used in a query" A 2 - “the percent of null values in a queried IS" A 3 - “the no. of objects returned by QAS when IS-complete" A 4 - “the no. of objects returned by QAS when IS-incomplete" (optimistic interpretation) A 5 - “the no. of objects returned by QAS based on rule-based chase algorithm" (pessimistic interpretation) A 6 - “the no. of bad objects retrieved" A 7 - “the no. of passes of rule-based chase algorithm"

Rules Discovery from partially Incomplete Information Systems

Data (Incomplete) Information System S = ( X, A, V ) X - finite set of objects, A - finite set of attributes, - set of their values. Assumption 1. For any 2. For any ,
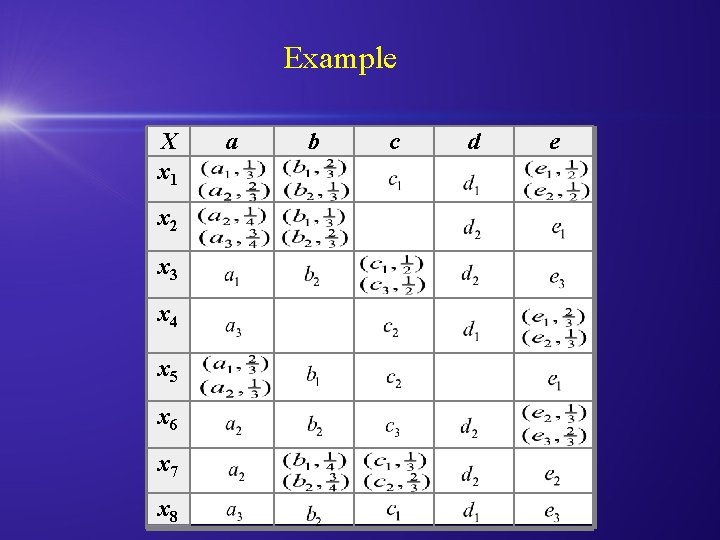
Example X x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 a b c d e

Algorithm ERID for Extracting Rules from partially Incomplete Information System X x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 a b c d e Goal: Describe e in terms of {a, b, c, d}

Algorithm ERID for Extracting Rules from partially Incomplete Information System X x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 a b c d e Goal: Describe e in terms of {a, b, c, d}

Algorithm ERID X x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 a b c d e Goal: Describe e in terms of {a, b, c, d} For the values of the decision attribute we have:

Algorithm ERID X x 1 x 2 a b c d e Goal: Describe e in terms of {a, b, c, d}. 2. Check the relationship “ ” x 3 between values of classification x 4 attributes {a, b, c, d} and values x 5 of decision attribute e x 6 x 7 x 8

Algorithm ERID X x 1 x 2 x 3 x 4 a b c d e Goal: Describe e in terms of {a, b, c, d} Let , We say that: iff support x 5 and confidence of the rule x 6 are above some threshold values. x 7 x 8 .

Algorithm ERID X x 1 x 2 x 3 x 4 a b c d e Goal: Describe e in terms of {a, b, c, d} Let , We say that: iff support x 5 and confidence of the rule x 6 are above some threshold values. x 7 x 8 How to define support and confidence of a rule ? .

Definition of Support and Confidence (by example) To define support and confidence of the rule a 1 e 3 we compute: Support of the rule: Support of the term a 1: Confidence of the rule:

Extracting Rules from partially Incomplete Information System (Algorithm ERID(λ 1, λ 2)) X x 1 x 2 a b c d e Goal: Describe e in terms of {a, b, c, d} Thresholds (provided by user): x 3 Minimal support x 4 Minimal confidence (λ 2 = ½) (λ 1 = 1) x 5 - marked negative x 6 - marked negative x 7 x 8 - marked positive
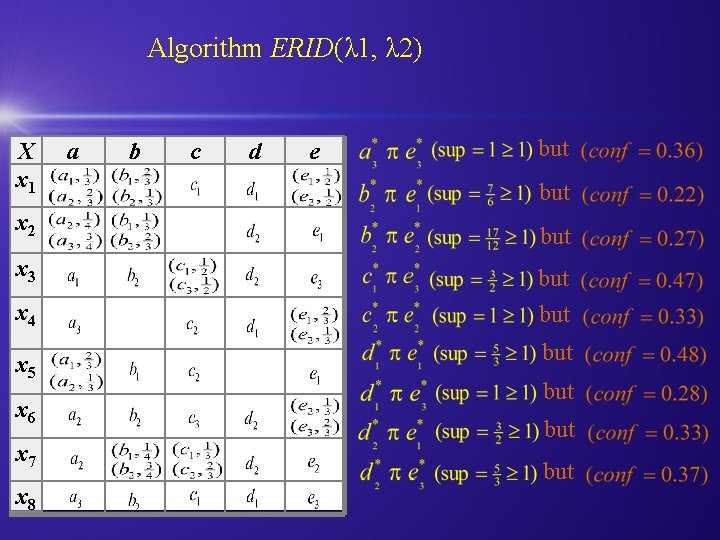
Algorithm ERID(λ 1, λ 2) X x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 a b c d e but but but
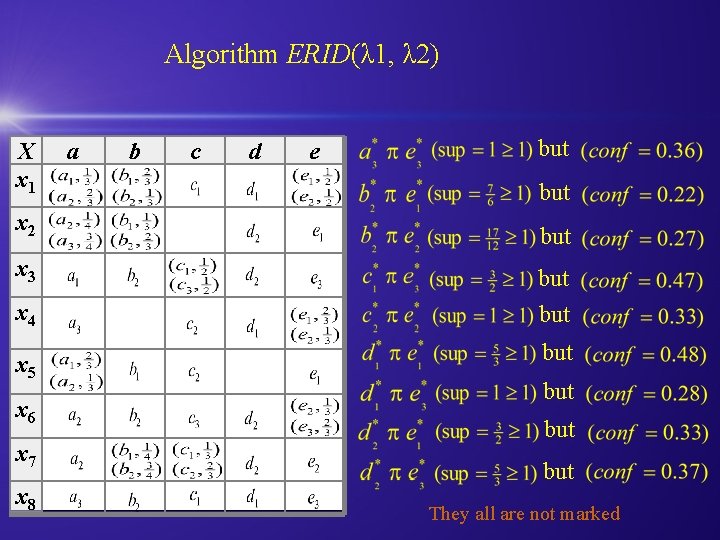
Algorithm ERID(λ 1, λ 2) X x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 a b c d e but but but They all are not marked

Algorithm ERID(λ 1, λ 2) X x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 a b c d e and

Algorithm ERID(λ 1, λ 2) X x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 a b c d e and They all are marked positive.

Algorithm ERID(λ 1, λ 2) X x 1 x 2 x 3 a b c d e and They all are marked positive. x 4 x 5 x 6 x 7 x 8 They all are marked negative.
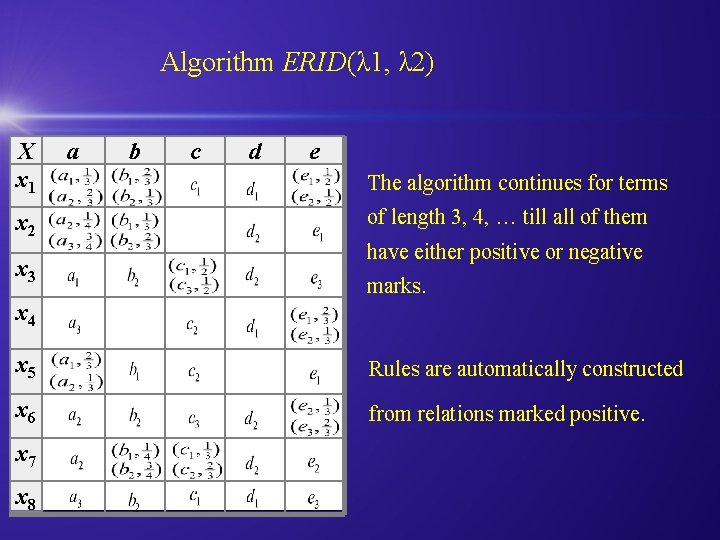
Algorithm ERID(λ 1, λ 2) X x 1 x 2 x 3 a b c d e The algorithm continues for terms of length 3, 4, … till all of them have either positive or negative marks. x 4 x 5 Rules are automatically constructed x 6 from relations marked positive. x 7 x 8

Algorithm Chase 2 (for Partially IIS)

Algorithm Chase 2 - partially incomplete information system of type λ, if S is incomplete and the following three conditions hold: q q q is defined for any ,

Algorithm Chase 2 S 1, S 2 - partially incomplete, both of type λ and both classifying the same sets of objects (from X) using the same sets of attributes (A) Let and The pair (S 1, S 2) satisfies containment relation Ψ (or Ψ(S 1)= S 2) if: q q We also denote that fact by
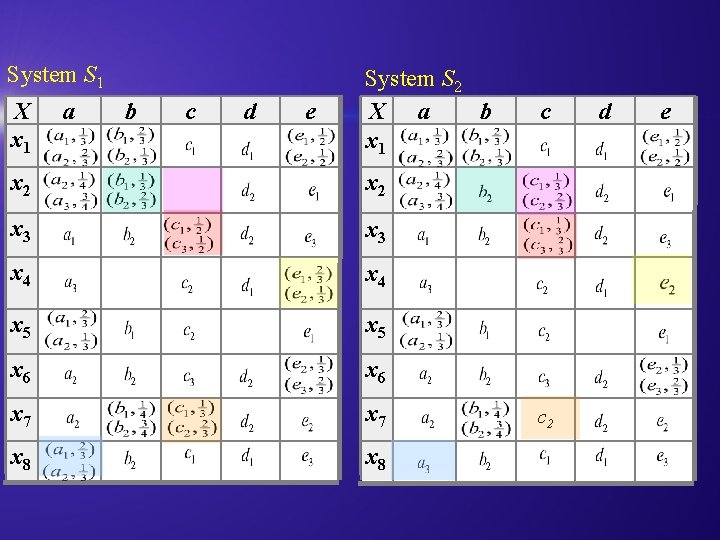
System S 1 X x 1 a b c d e System S 2 X a b x 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 c c 2 d e

Assumptions: - information system of type λ - set of all pairwise q q independent rules extracted by ERID from S q NS(t) - standard interpretation of term t in S, meaning that: § , for any § § where for any , § § q In(A) = {a 1, … , ak} - incomplete attributes in S we have:

Algorithm Chase 2 (S, In(A), L(D)). . . . for all do begin if and is a maximal subset of rules from L(D) such that then if then begin end if then . . . . end pj: = pj +nj; /containment relation holds between aj(x), [bj(x)/pj]/

X x 1 a b c d x 2 x 3 x 4 x 5 x 6 x 7 x 8 Incomplete Information System S of type λ = 0. 3 e ERID(λ 1, λ 2) λ 1=1, λ 2=0. 5

X x 1 a b c d x 2 e ERID(λ 1, λ 2) λ 1=1, λ 2=0. 5 Algorithm Chase 2 will try to replace x 3 by enew(x 1) = {(e 1, ), (e 2, ), (e 3, )}. x 4 x 5 We will show that Ψ(e(x 1)) = enew(x 1) (the value e(x 1) will be changed by Chase 2). x 6 x 7 x 8 Incomplete Information System S of type λ = 0. 3

X x 1 a b c d e For x 1: x 2 x 3 x 4 we have: x 5 x 6 x 7 x 8 Incomplete Information System S of type λ = 0. 3 Because the confidence assigned to e 3 is below the threshold λ, then only two values remain: (e 1, 0. 48), (e 2, 0. 97). The value of attribute e assigned to x 1 is: {(e 1, 0. 33), (e 2, 0. 67)}.

Distributed Chase Algorithm (Chase 3)

Let: - distributed autonomous information systems - information system for any (I - set of sites) - knowledge-base at site - set of (k, i)-rules (constructed at site k and sent to site i)

Strategy for constructing knowledge-base and Algorithm Chase 3 Notation: q. S=[a, b, c : d, e] - request by S for definitions of a, b, c with additional information that d, e are complete attributes in S.
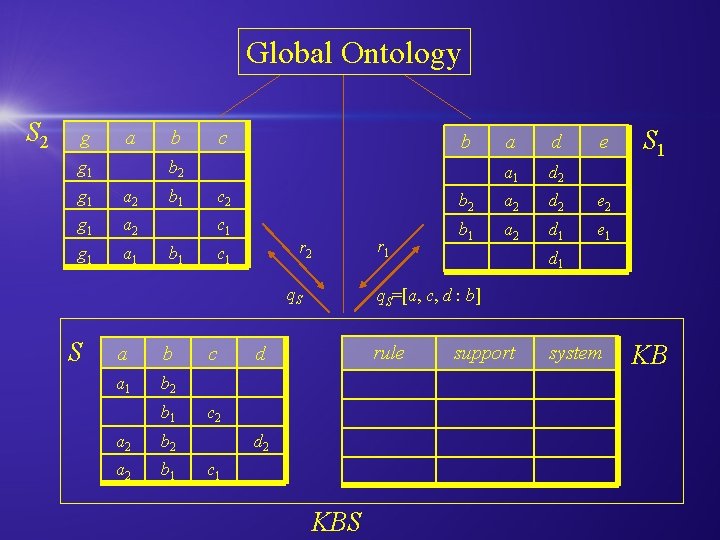
Global Ontology S 2 g a g 1 b c b b 2 g 1 a 1 b 1 a b a 1 b 2 b 1 a 2 b 2 a 2 b 1 d a 1 d 2 e c 2 b 2 a 2 d 2 e 2 c 1 b 1 a 2 d 1 e 1 r 2 c 1 q. S S a c S 1 d 1 q. S=[a, c, d : b] rule d c 2 d 2 c 1 KBS support system KB
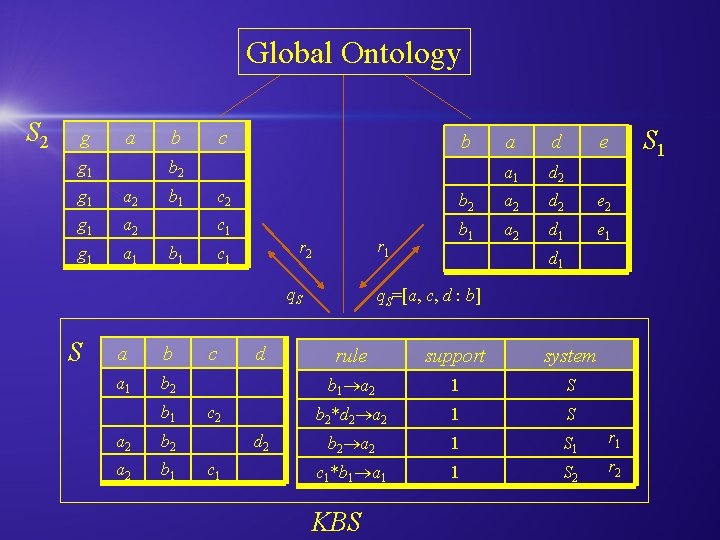
Global Ontology S 2 g a g 1 b c b b 2 g 1 a 1 b 1 a b a 1 b 2 b 1 a 2 b 2 a 2 b 1 d e a 1 d 2 c 2 b 2 a 2 d 2 e 2 c 1 b 1 a 2 d 1 e 1 r 2 c 1 q. S S a c d c 2 d 2 c 1 d 1 q. S=[a, c, d : b] rule support system b 1 a 2 1 S b 2*d 2 a 2 1 S b 2 a 2 1 S 1 r 1 c 1*b 1 a 1 1 S 2 r 2 KBS S 1

Assumption: Di - granularity level of values of attributes used in rules from Di may differ from the granularity level of values of attribute used in descriptions of objects in Chase 3 algorithm to be applicable to Si has to be based on rules from Di satisfying the following two conditions: . q attribute value used in the decision part of a rule has the granularity level either equal to or finer than the granularity level of the corresponding attribute in Si q the granularity level of any attribute used in the classification part of a rule is either equal or softer than the granularity level of the corresponding attribute in Si .
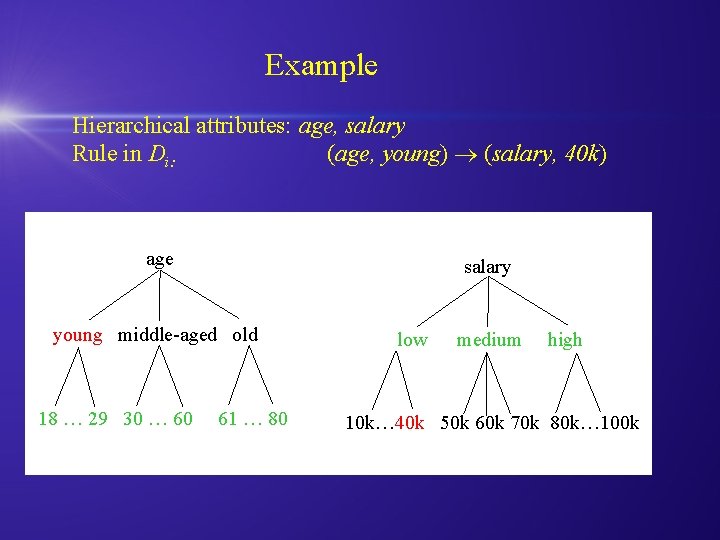
Example Hierarchical attributes: age, salary Rule in Di: (age, young) (salary, 40 k) age salary young middle-aged old 18 … 29 30 … 60 61 … 80 low medium high 10 k… 40 k 50 k 60 k 70 k 80 k… 100 k

Algorithm Chase 3 (Construction of new Di followed by Chase 2) Assumption: tuple t in Si supports rule . Two cases: 1. An overlapping attribute between rule and the tuple is the decision attribute in . If two attributes, involved in that match, have different granularities, then the decision value d has to be replaced by a softer value which granularity will match the granularity of the corresponding attribute in Si. 2. An overlapping attribute between rule and the tuple is the classification attribute in . If two attributes, involved in that match, have different granularities, then the value of attribute a has to be replaced by a finer value which granularity will match the granularity of a in Si.

Chase 4 (All Information Systems are equally involved in chase)
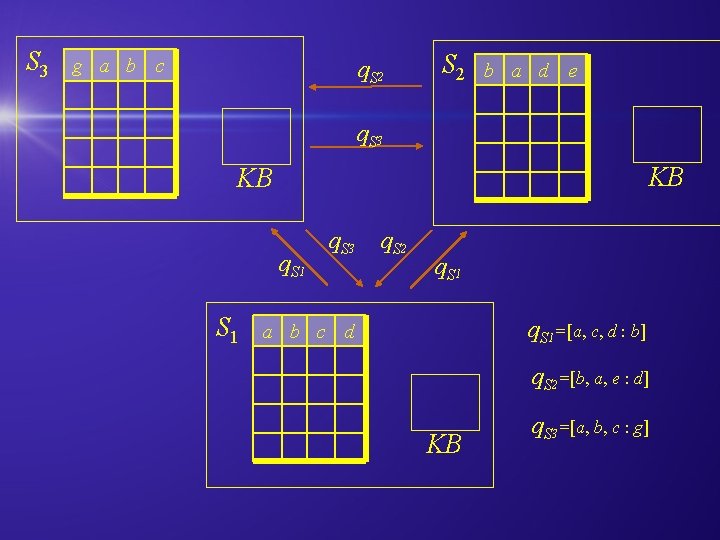
S 3 g a b c q. S 2 b a d e q. S 3 KB KB q. S 1 q. S 3 q. S 2 q. S 1=[a, c, d : b] a b c d q. S 2=[b, a, e : d] KB q. S 3=[a, b, c : g]
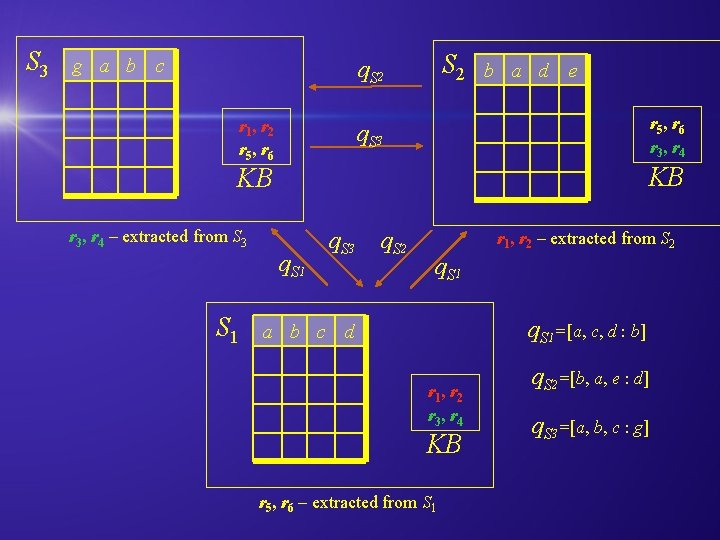
S 3 g a b c S 2 q. S 2 r 1 , r 2 r 5 , r 6 b a d e r 5 , r 6 r 3 , r 4 q. S 3 KB KB r 3, r 4 – extracted from S 3 q. S 1 q. S 3 q. S 2 r 1, r 2 – extracted from S 2 q. S 1=[a, c, d : b] a b c d r 1 , r 2 r 3 , r 4 KB r 5, r 6 – extracted from S 1 q. S 2=[b, a, e : d] q. S 3=[a, b, c : g]

- Slides: 56