Charles van Marrewijk 2006 1 INTERNATIONAL ECONOMICS THEORY

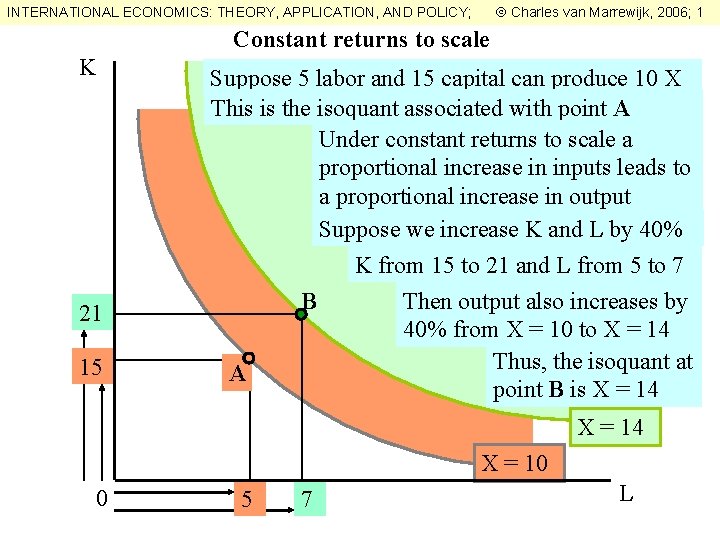
Charles van Marrewijk, 2006; 1 INTERNATIONAL ECONOMICS: THEORY, APPLICATION, AND POLICY; Constant returns to scale K 21 15 Suppose 5 labor and 15 capital can produce 10 X This is the isoquant associated with point A Under constant returns to scale a proportional increase in inputs leads to a proportional increase in output Suppose we increase K and L by 40% K from 15 to 21 and L from 5 to 7 Then output also increases by B 40% from X = 10 to X = 14 Thus, the isoquant at A point B is X = 14 X = 10 0 5 7 L

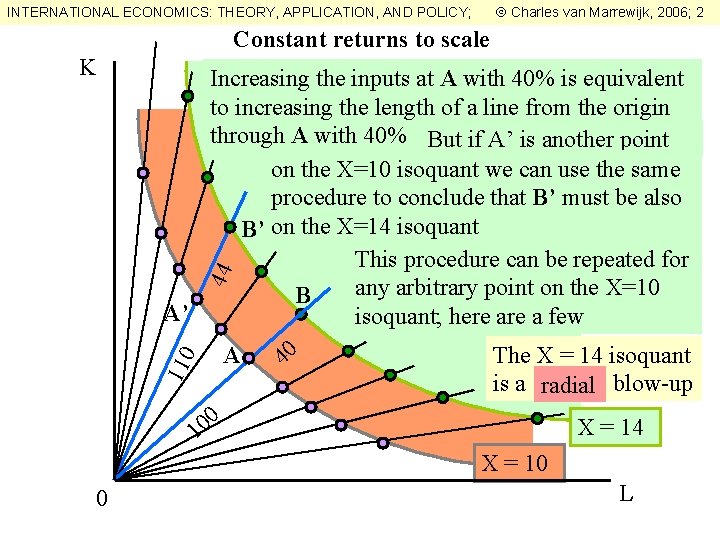
INTERNATIONAL ECONOMICS: THEORY, APPLICATION, AND POLICY; Charles van Marrewijk, 2006; 2 Constant returns to scale Increasing the inputs at A with 40% is equivalent to increasing the length of a line from the origin through A with 40% But if A’ is another point on the X=10 isoquant we can use the same procedure to conclude that B’ must be also B’ on the X=14 isoquant This procedure can be repeated for any arbitrary point on the X=10 B A’ isoquant; here a few The X = 14 isoquant A 40 is a radial blow-up 0 0 X = 14 1 X = 10 L 110 44 K 0

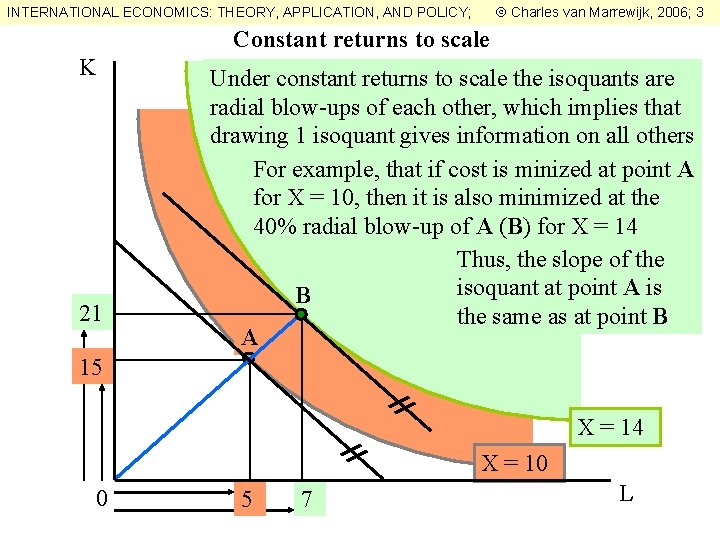
Charles van Marrewijk, 2006; 3 INTERNATIONAL ECONOMICS: THEORY, APPLICATION, AND POLICY; Constant returns to scale K 21 Under constant returns to scale the isoquants are radial blow-ups of each other, which implies that drawing 1 isoquant gives information on all others For example, that if cost is minized at point A for X = 10, then it is also minimized at the 40% radial blow-up of A (B) for X = 14 Thus, the slope of the isoquant at point A is B the same as at point B A 15 X = 14 X = 10 0 5 7 L

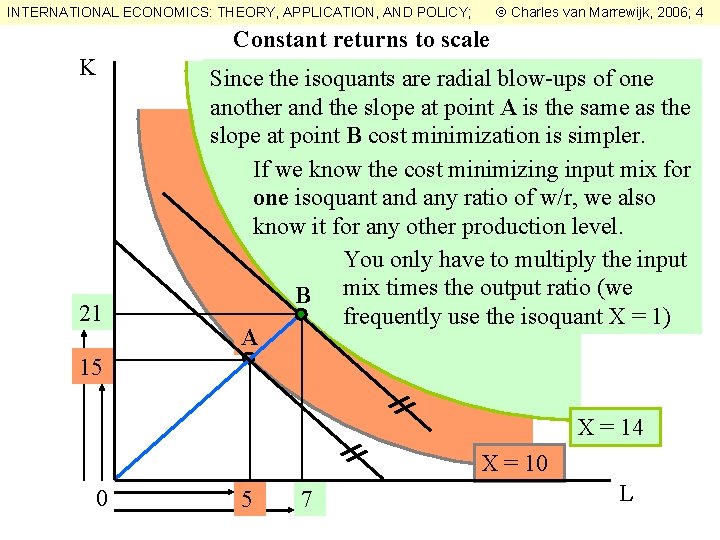
Charles van Marrewijk, 2006; 4 INTERNATIONAL ECONOMICS: THEORY, APPLICATION, AND POLICY; Constant returns to scale K 21 Since the isoquants are radial blow-ups of one another and the slope at point A is the same as the slope at point B cost minimization is simpler. If we know the cost minimizing input mix for one isoquant and any ratio of w/r, we also know it for any other production level. You only have to multiply the input B mix times the output ratio (we frequently use the isoquant X = 1) A 15 X = 14 X = 10 0 5 7 L