Charles Ragins Qualitative Comparative Analysis Boolean Algebra Either

Charles Ragin’s Qualitative Comparative Analysis • • Boolean Algebra Either A or B = A+B Example: To purchase this car (P) you need either cash (A) or credit (B) P=A+B A and B =A*B Example: To drive this car (D) you have to have both a license (L) and an insurance (I) D=L*I If you also have to buy the car then D=P*L*I D=(A+B)*L*I=A*L*I+B*L*I in words: You either have to have cash and a license and insurance or you have to have credit and a license and insurance Notation: not P is p (not A is a etc. ) Example: p=a*b d=? ? ? d=l+i

Charles Ragin’s Qualitative Comparative Analysis (cont. ) • TRUTH TABLE • • • • Example: Causes of regime Downfall A=conflict between older and younger military officers B= Death of a powerful dictator C=CIA dissatisfaction with the regime 0=No 1=Yes A B C D=Downfall # of cases (total=32 cases) 0 0 9 1 0 0 1 2 0 1 4 0 0 1 1 3 1 1 0 1 2 0 1 1 1 7 1 0 1 1 2 1 1 3 • D=Abc+a. Bc+ab. C+ABc+a. BC+Ab. C+ABC • D=A+B+C

Simplifying Boolean Expressions • RULE: Look for two terms that are the same except for the fact that one element is present in one and absent in the other. – E. g. ABC and ABc are such pair of terms. AB works with or without C. So C is irrelevant, and both can be simplified into AB. – Similarly, ABcd and ABc. D are pairs and both can be simplified into ABc. – BUT ABC and a. Bc are not pairs, and nor are ABc and ABd. To find the pairs, 1. create a table of all the terms and find the pairs, indicate their simplified forms put 0 otherwise. (The table will have content only above the diagonal. ) 2. See if any term is left without a pair. Write that down. That term will enter the final equation. 3. Take the simplified forms, create a table and look for pair again. 4. Repeat 2. 5. Repeat 3 and 4 until you have only terms with a single element. (With 3 causes you will have two tables. With 4 you will have three. In general, you will have k 1 tables where k is the number of causes. )

Simplifying D=Abc+a. Bc+ab. C+ABc+a. BC+Ab. C+ABC

Checking Results • D=Abc+a. Bc+ab. C+ABc+a. BC+Ab. C+ABC • Simplifies to • D=A+B+C • Checking Results – Create a table of the original terms by the terms in the simplified form. – Write a 1 if the simplified term is part of an original term (write 0 otherwise). – Does each original term have at least a 1?
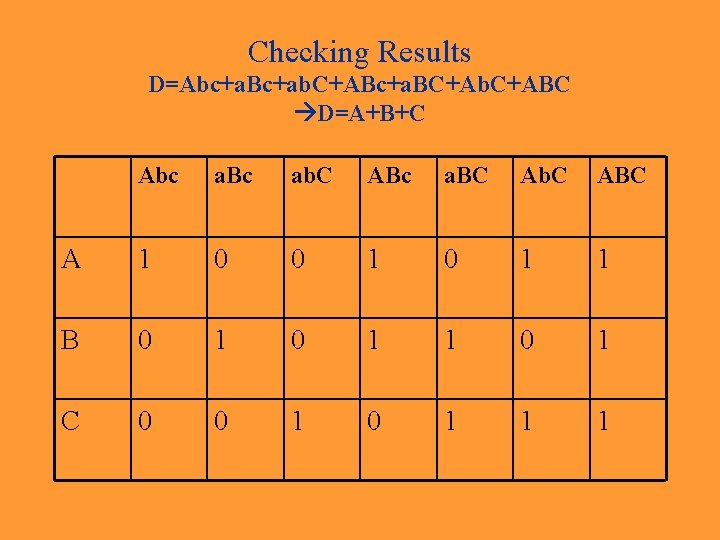
Checking Results D=Abc+a. Bc+ab. C+ABc+a. BC+Ab. C+ABC D=A+B+C Abc a. Bc ab. C ABc a. BC Ab. C ABC A 1 0 0 1 1 B 0 1 1 0 1 C 0 0 1 1 1

Charles Ragin’s Qualitative Comparative Analysis (cont. ) • • • • • A= booming product market B= threat of sympathy strikes C= Large Strike Fund A B C 1 0 1 0 1 1 1 1 0 0 1 0 1 1 0 0 0 S=Ab. C+a. Bc+ABC » » Example: Causes of successful strikes S=Success 1 1 0 0 Number of cases 5 4 3 2 2 2 1 3 if both a. Bc and ABc work we can ignore A/a if B is present but C is absent ( c ) Bc if both Ab. C and ABC work we can ignore B/b if AC are present AC if both ABc and ABC work we can ignore C/c if AB are present AB S=Bc+AC+AB This further simplifies to S=Bc+AC (see later)

Simplifying S=Ab. C+a. Bc+ABC

Checking Results S=Ab. C+a. Bc+ABC S=Bc+AC+AB

Simplifying even further • The previous table revealed that we can drop AB and still each original term will have at least one 1. So the best and final model is: • S=Bc+AC

• • • • • • Example: Causes of successfully passing the class A= Having taken other sociology classes B= Having studied a lot (more than 3 hours a week) C= Having attended the lectures regularly D= Having a roommate/friend who took this class before A B C D S=Success Number (Total: 70) 0 0 0 3 1 0 0 5 0 1 0 0 1 2 0 0 1 0 0 4 0 0 0 1 0 7 1 1 0 0 1 4 1 0 1 5 1 0 0 1 1 8 0 1 1 0 1 3 0 0 1 1 0 4 0 1 1 4 1 1 1 0 1 9 1 1 0 1 1 3 1 0 1 1 1 5 0 1 1 2 1 1 1 2 S= a. Bcd+ABcd+ Ab. Cd+Abc. D+a. BCd+ a. Bc. D+ABCd+ABc. D+Ab. CD+a. BCD+ABCD S=B+AC+AD

Simplifying S= a. Bcd+ABcd+ Ab. Cd+Abc. D+a. BCd+ a. Bc. D+ABCd+ABc. D+Ab. CD+a. BCD+ABCD



Checking S= a. Bcd+ABcd+ Ab. Cd+Abc. D+a. BCd+ a. Bc. D+ABCd+ABc. D+Ab. CD+a. BCD+ABCD B+AC+AD
- Slides: 15