Charging and Discharging a Capacitor Complete the activity

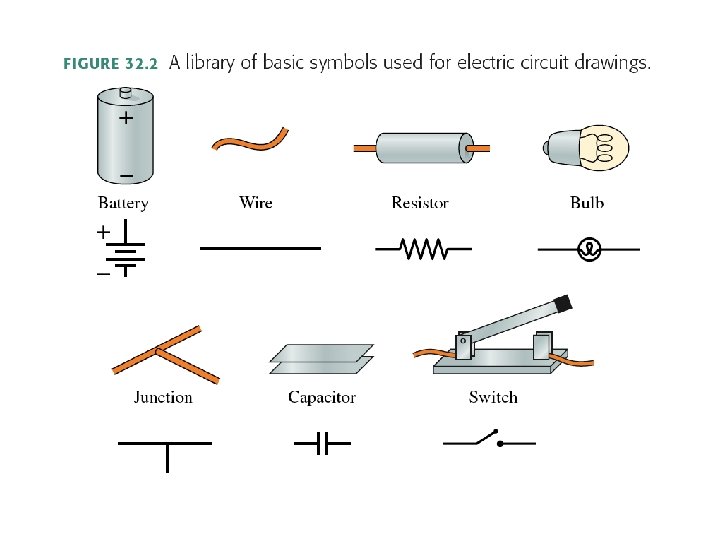












- Slides: 28

Charging and Discharging a Capacitor • Complete the activity on charging and discharging capacitors located under Activities on the website • sites. google. com/site/sienaphys 140 spring 2011/activities/cha rging-and-discharging-a-capacitor



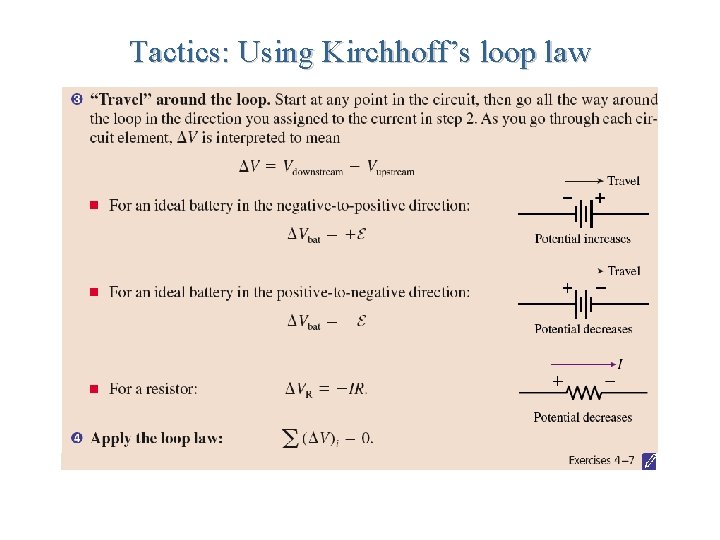
Tactics: Using Kirchhoff’s loop law


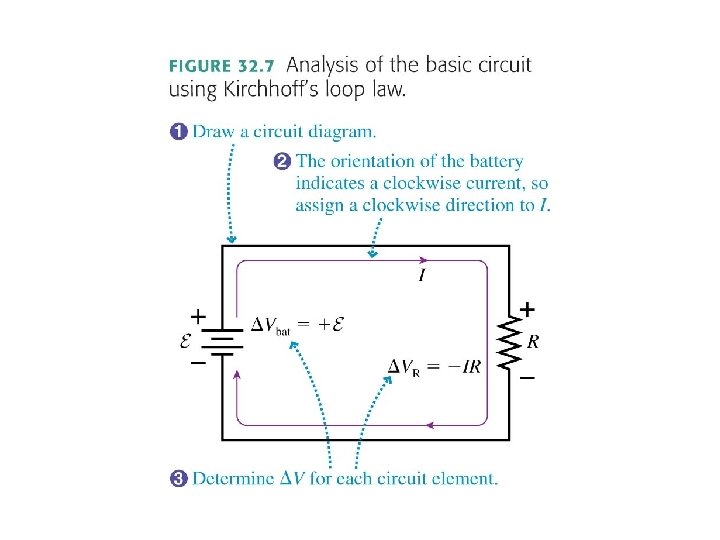
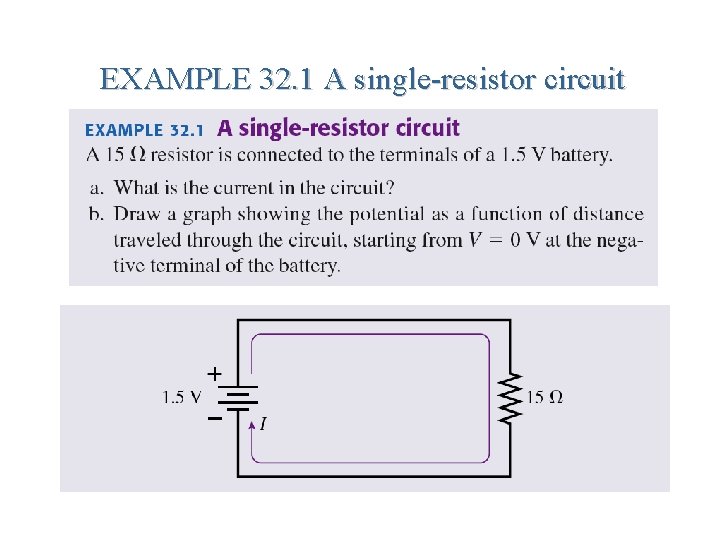
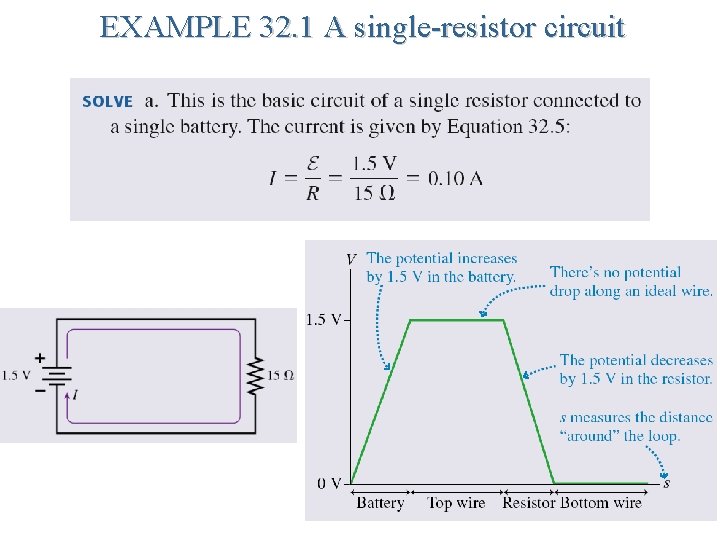
EXAMPLE 32. 1 A single-resistor circuit

EXAMPLE 32. 1 A single-resistor circuit

Energy and Power The power supplied by a battery is The units of power are J/s, or W. The power dissipated by a resistor is Or, in terms of the potential drop across the resistor

EXAMPLE 32. 4 The power of light

EXAMPLE 32. 4 The power of light

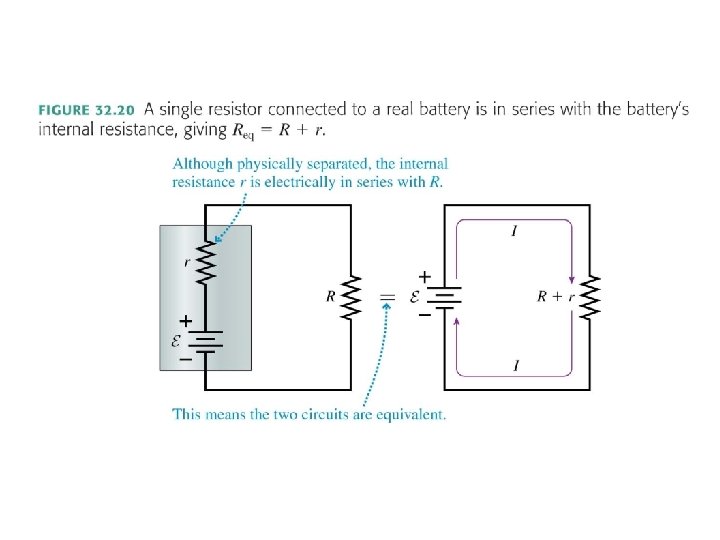
Series Resistors • Resistors that are aligned end to end, with no junctions between them, are called series resistors or, sometimes, resistors “in series. ” • The current I is the same through all resistors placed in series. • If we have N resistors in series, their equivalent resistance is The behavior of the circuit will be unchanged if the N series resistors are replaced by the single resistor Req.


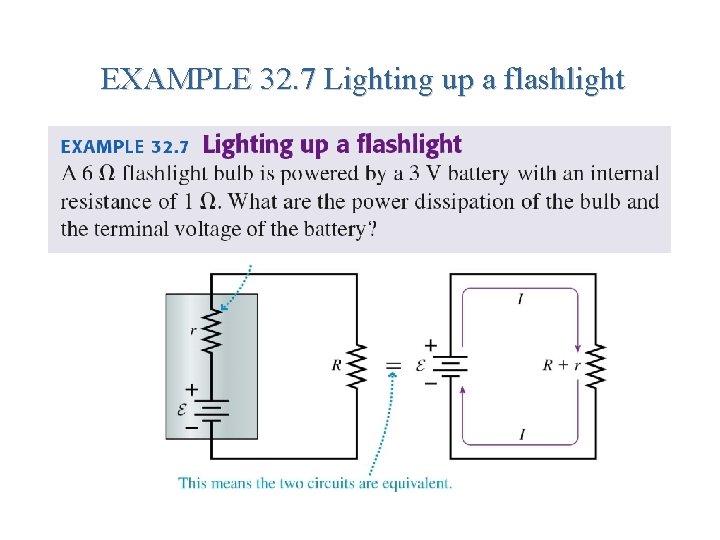
EXAMPLE 32. 7 Lighting up a flashlight

EXAMPLE 32. 7 Lighting up a flashlight

Parallel Resistors • Resistors connected at both ends are called parallel resistors or, sometimes, resistors “in parallel. ” • The left ends of all the resistors connected in parallel are held at the same potential V 1, and the right ends are all held at the same potential V 2. • The potential differences ΔV are the same across all resistors placed in parallel. • If we have N resistors in parallel, their equivalent resistance is The behavior of the circuit will be unchanged if the N parallel resistors are replaced by the single resistor Req.

Series and Parallel Resistors

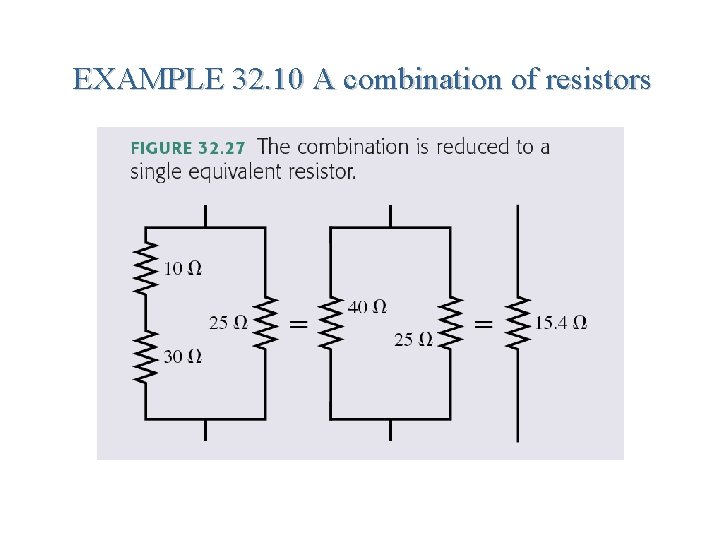
EXAMPLE 32. 10 A combination of resistors QUESTION:

EXAMPLE 32. 10 A combination of resistors


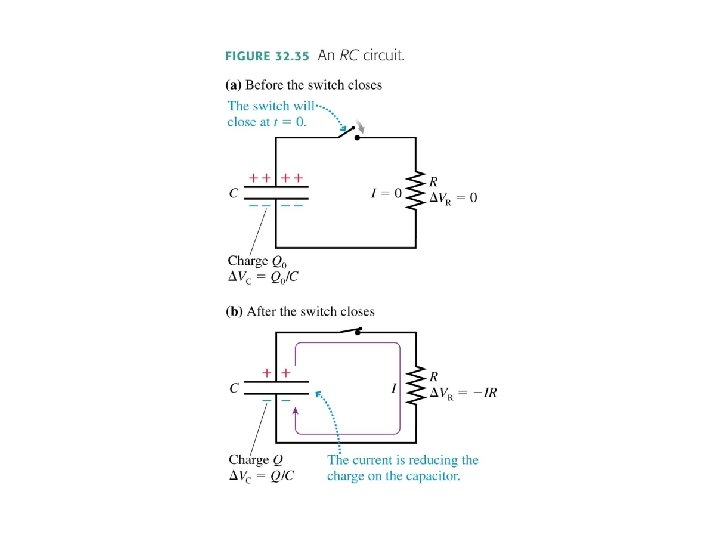
RC Circuits • Consider a charged capacitor, an open switch, and a resistor all hooked in series. This is an RC Circuit. • The capacitor has charge Q 0 and potential difference ΔVC = Q 0/C. • There is no current, so the potential difference across the resistor is zero. • At t = 0 the switch closes and the capacitor begins to discharge through the resistor. • The capacitor charge as a function of time is where the time constant τ is

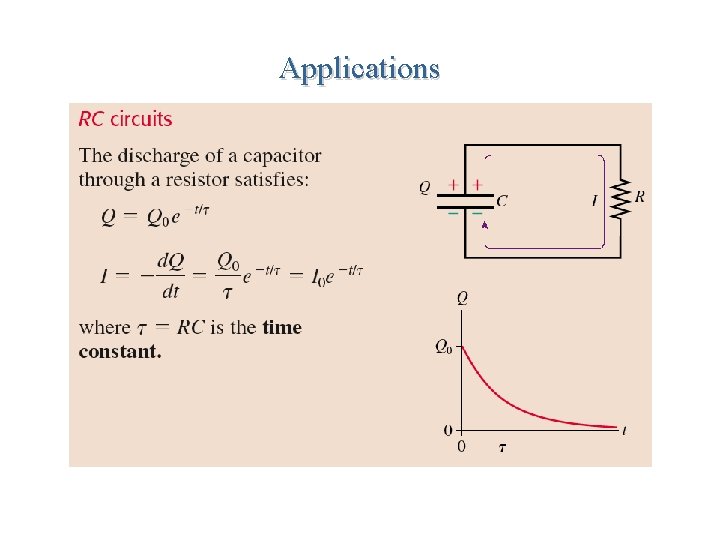
Applications

EXAMPLE 32. 14 Exponential decay in an RC circuit QUESTION:

EXAMPLE 32. 14 Exponential decay in an RC circuit

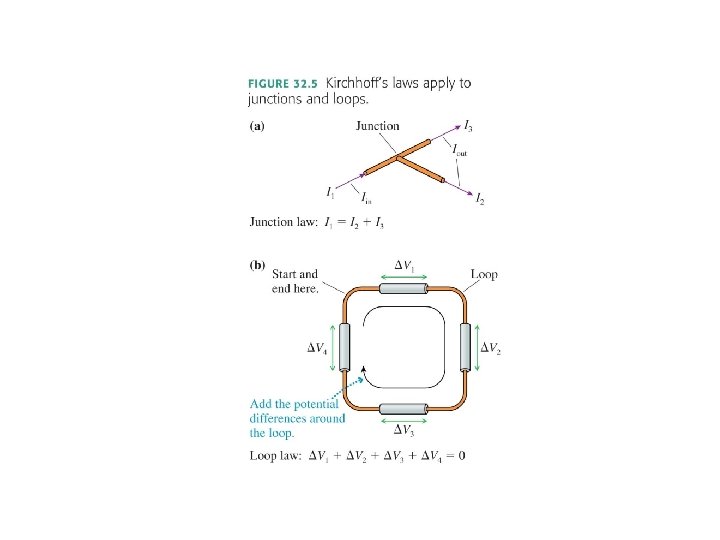
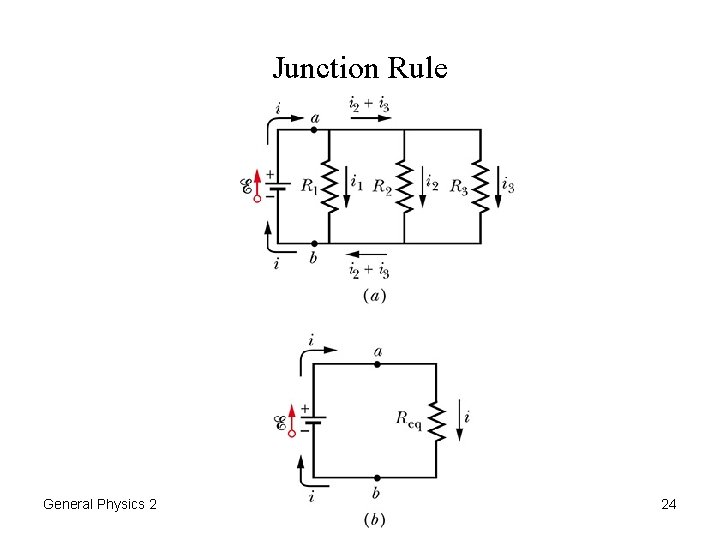
Junction Rule General Physics 2 Circuits 24

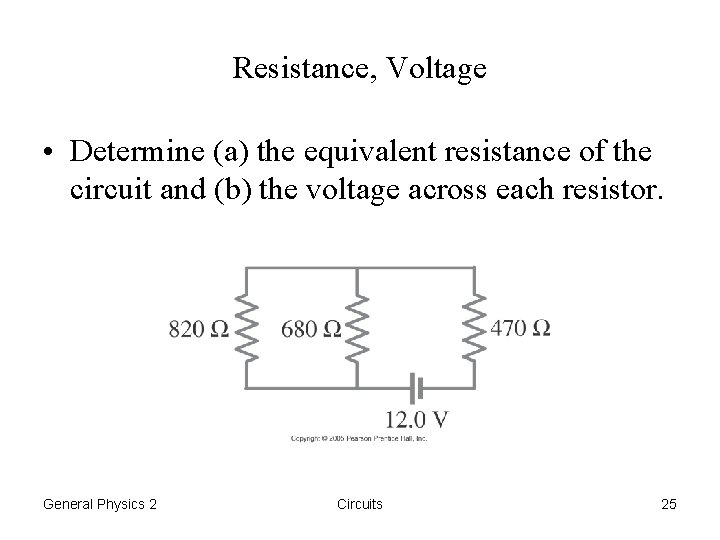
Resistance, Voltage • Determine (a) the equivalent resistance of the circuit and (b) the voltage across each resistor. General Physics 2 Circuits 25

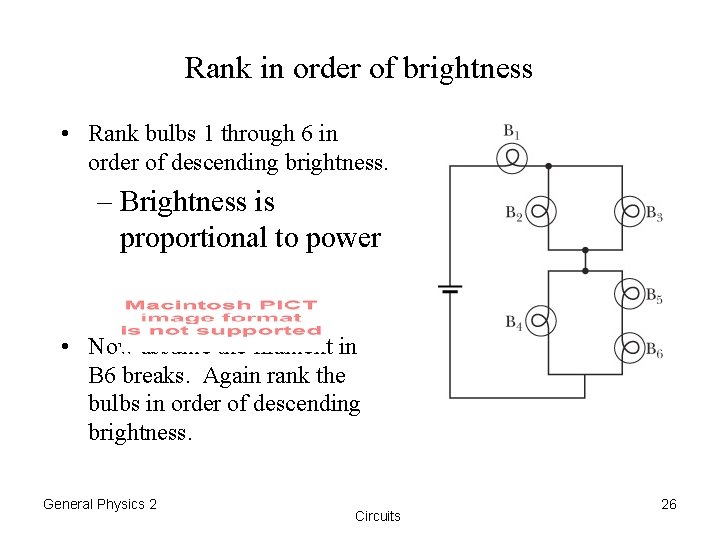
Rank in order of brightness • Rank bulbs 1 through 6 in order of descending brightness. – Brightness is proportional to power • Now assume the filament in B 6 breaks. Again rank the bulbs in order of descending brightness. General Physics 2 Circuits 26

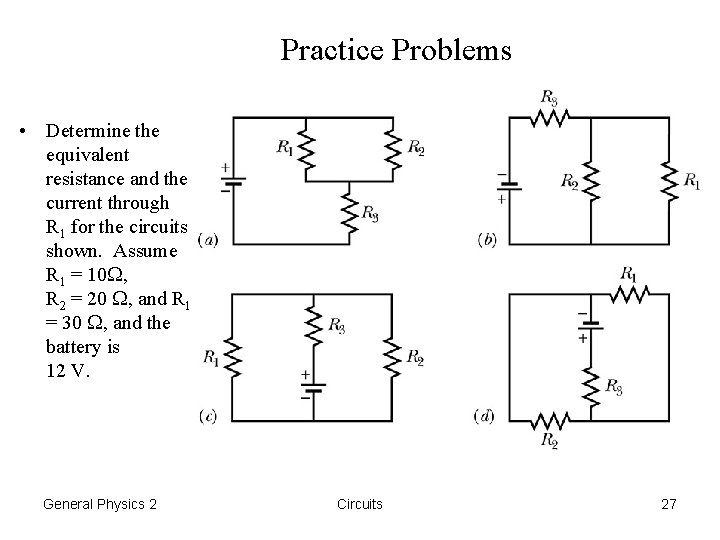
Practice Problems • Determine the equivalent resistance and the current through R 1 for the circuits shown. Assume R 1 = 10 , R 2 = 20 , and R 1 = 30 , and the battery is 12 V. General Physics 2 Circuits 27

Activities • Exploration of Physics – E&M – Resistive circuits – Do each of the 5 circuits – set all to 50 ohms – Calculate I, V, and P for each resistor and then check answers in the program General Physics 2 Current & Resistance 28