Characterization of Forecast Error using Singular Value Decomposition




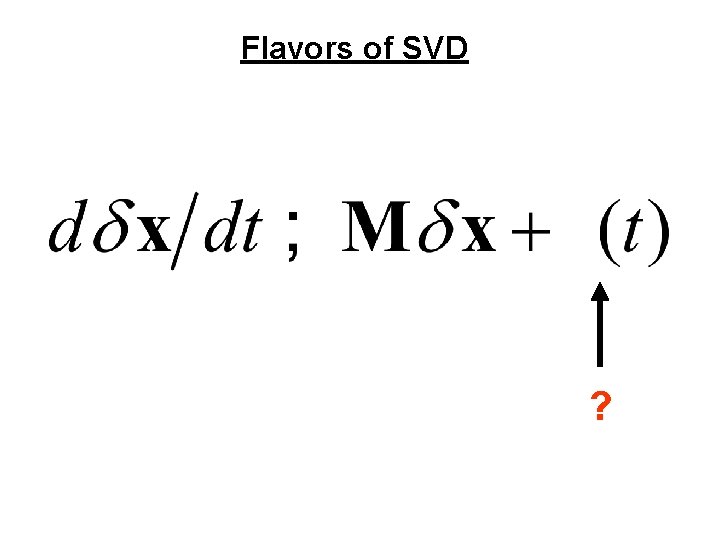









- Slides: 37

Characterization of Forecast Error using Singular Value Decomposition Andy Moore and Kevin Smith University of California Santa Cruz Hernan Arango Rutgers University

Outline • An overview of singular value decomposition (SVD) • Flavors of SVD • Duality of SVD • Norms • Unstable jet • California Current

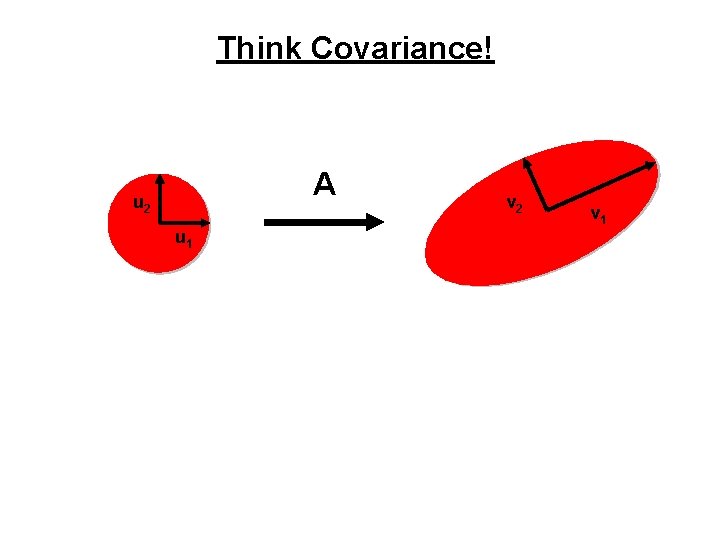
Singular Value Decomposition (SVD) A generalization of eigenvectors for rectangular matrices. Square Matrix: Rectangular Matrix: Right singular vectors: Left singular vectors: Important rank/ dimension info

Think Covariance! A u 2 u 1 v 2 v 1

SVD and “Model” Errors State vector: Perfect model: Imperfect model: Errors: TLM: Tangent linear model

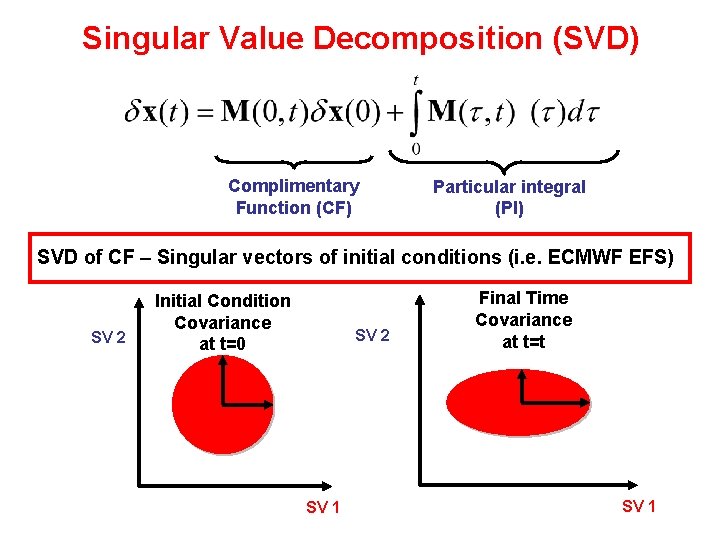
Singular Value Decomposition (SVD) Complimentary Function (CF) Particular integral (PI) SVD of CF – Singular vectors of initial conditions (i. e. ECMWF EFS) SV 2 Initial Condition Covariance at t=0 SV 2 SV 1 Final Time Covariance at t=t SV 1

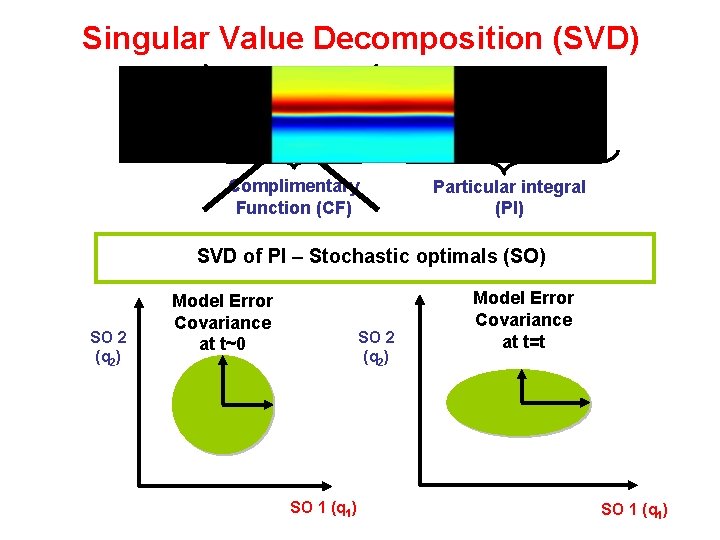
Singular Value Decomposition (SVD) Complimentary Function (CF) Particular integral (PI) SVD of PI – Stochastic optimals (SO) SO 2 (q 2) Model Error Covariance at t~0 SO 2 (q 2) SO 1 (q 1) Model Error Covariance at t=t SO 1 (q 1)

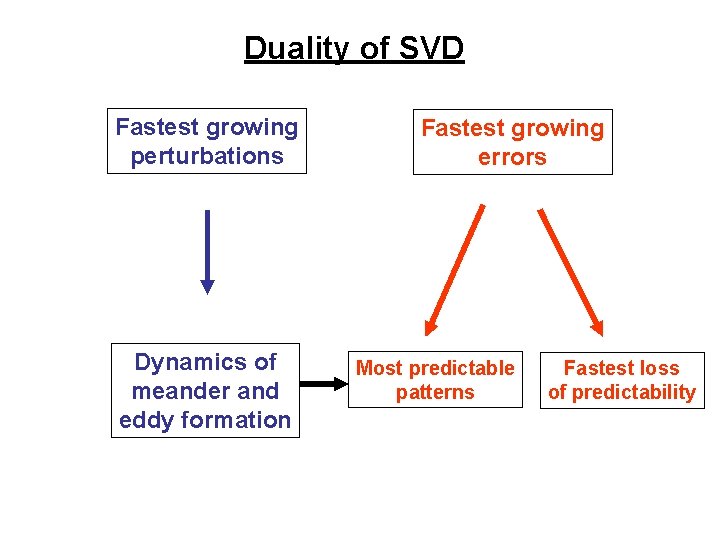
Duality of SVD Fastest growing perturbations Dynamics of meander and eddy formation Fastest growing errors Most predictable patterns Fastest loss of predictability
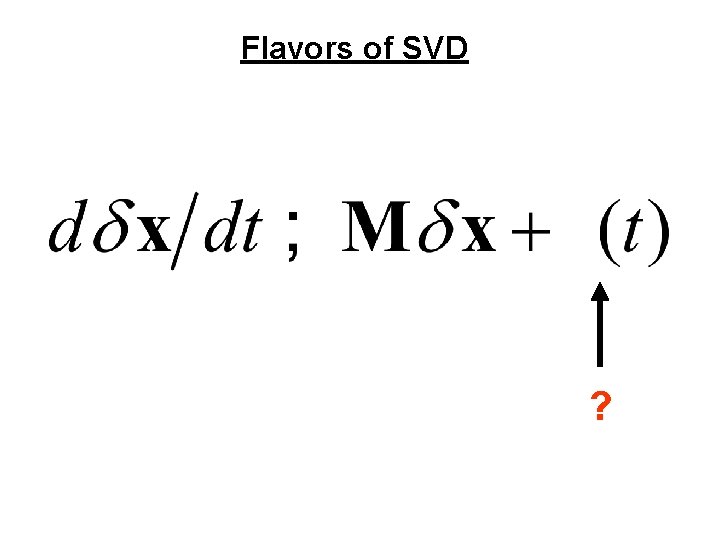
Flavors of SVD ?

Flavors of SVD Initial condition error: Find the e 0 that maximizes: FInal time norm Subject to the constraint: Initial time norm Equivalent to the generalized eigenvalue problem: and SVD of:

Illustrative Example – A Zonal Jet 360 km 600 km Initial SV 500 m deep, f=10 -4, b=0, Dx-15 km, Dz=100 m Eastward Gaussian jet, 40 km width, 1. 6 ms-1 SV time interval = 2 days. Energy norm, P=C. SVD: Forcing SV SVD: Stoch Opt (white) SVD: Stoch Opt (red) SVD: tc= 2 days

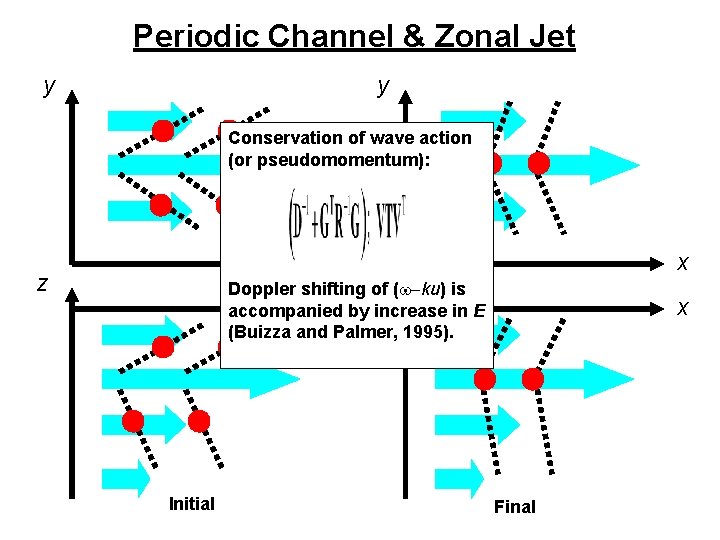
Periodic Channel & Zonal Jet y y Conservation of wave action (or pseudomomentum): x z x Doppler shifting z of (w-ku) is accompaniedxby increase in E (Buizza and Palmer, 1995). Initial x Final

Baroclinically Unstable Jet t=50 days SST 2000 km t=0 Dx=10 km, f=-10 -4, b=1. 6× 10 -11 1000 km SH

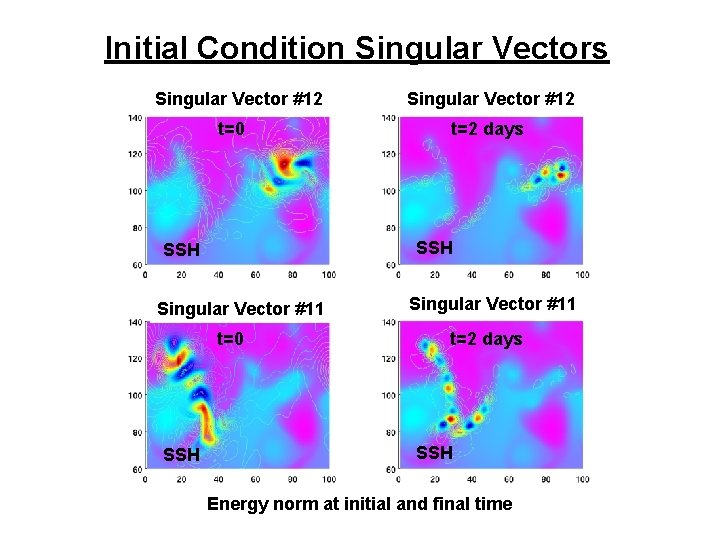
Initial Condition Singular Vectors Singular Vector #12 t=0 t=2 days SSH Singular Vector #11 t=0 SSH Singular Vector #12 Singular Vector #11 t=2 days SSH Energy norm at initial and final time


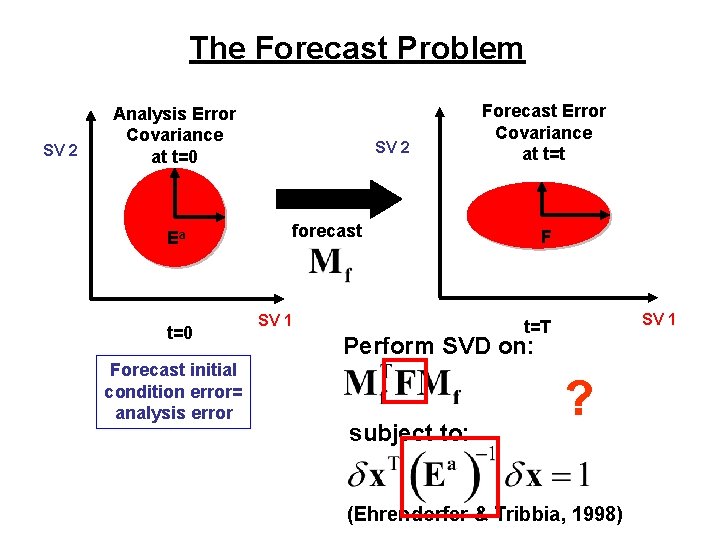
The Forecast Problem SV 2 Analysis Error Covariance at t=0 Ea t=0 Forecast initial condition error= analysis error SV 2 Forecast Error Covariance at t=t forecast SV 1 F SV 1 t=T Perform SVD on: subject to: ? (Ehrendorfer & Tribbia, 1998)

The Inverse Analysis Error Covariance, (Ea)-1 Inverse Analysis error covariance Prior Error Cov. Hessian matrix Adjoint of ROMS Obs Error Cov. Tangent of ROMS Hessian matrix Primal space Lanczos vector expansion from 4 D-Var The number Lanczos vectors = number of 4 D-Var inner-loops

The Forecast Error Covariance, F Experience in numerical weather prediction at ECMWF suggests that F=E is a good choice (Buizza and Palmer, 1995). We will assume the same here… … more on this later however…

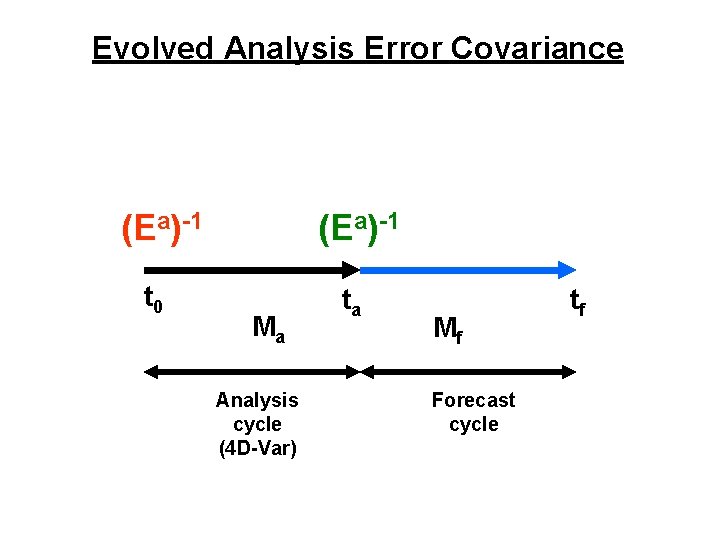
Evolved Analysis Error Covariance (Ea)-1 t 0 (Ea)-1 Ma Analysis cycle (4 D-Var) ta Mf Forecast cycle tf

Evolved Analysis Error Covariance We actually need the analysis error at the end of the analysis cycle: so we need the time evolved Lanczos vectors, Ve. but Reorthonormalize using Gramm-Schmidt: where: and

Hessian Singular Vectors Find the x that maximizes forecast error Subject to the constraint that (Barkmeijer et al, 1998) But Solve the equivalent eigenvalue problem: where and The dimension of the problem is reduced to the # of 4 D-Var innerloops whole spectrum. (Cholesky factorization of T) and where A+ is the right generalized inverse, and

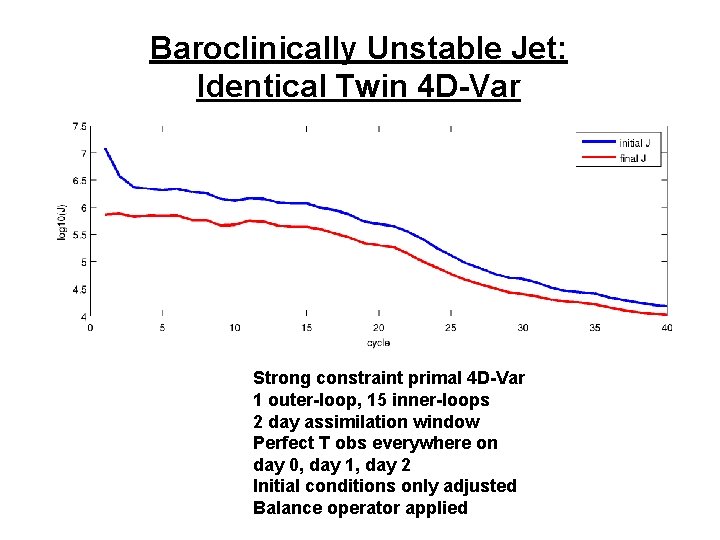
Baroclinically Unstable Jet: Identical Twin 4 D-Var Strong constraint primal 4 D-Var 1 outer-loop, 15 inner-loops 2 day assimilation window Perfect T obs everywhere on day 0, day 1, day 2 Initial conditions only adjusted Balance operator applied

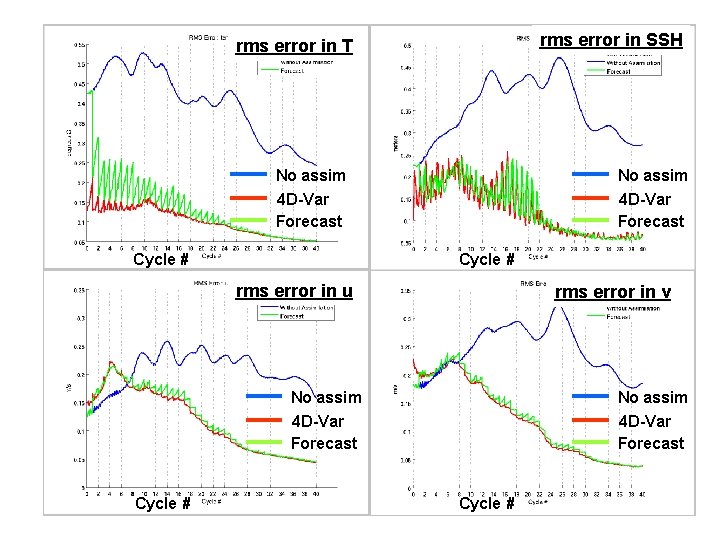
rms error in SSH rms error in T No assim 4 D-Var Forecast Cycle # rms error in u rms error in v No assim 4 D-Var Forecast Cycle #

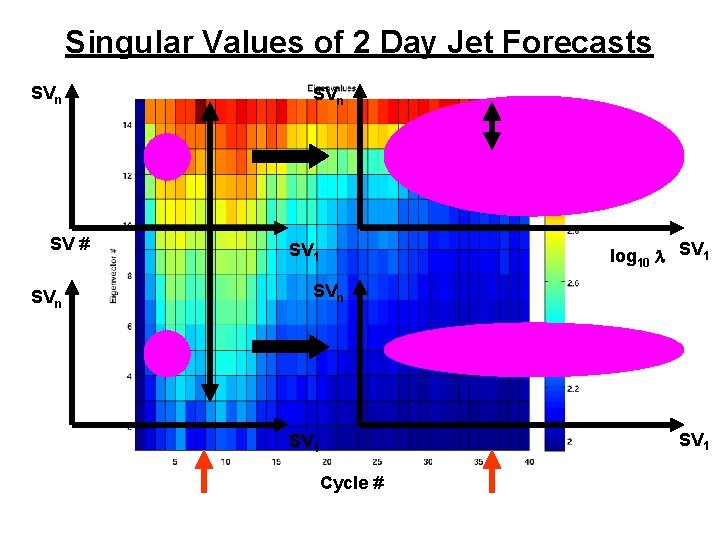
Singular Values of 2 Day Jet Forecasts SVn SV # SVn SV 1 log 10 l SV 1 SVn SV 1 Cycle # SV 1

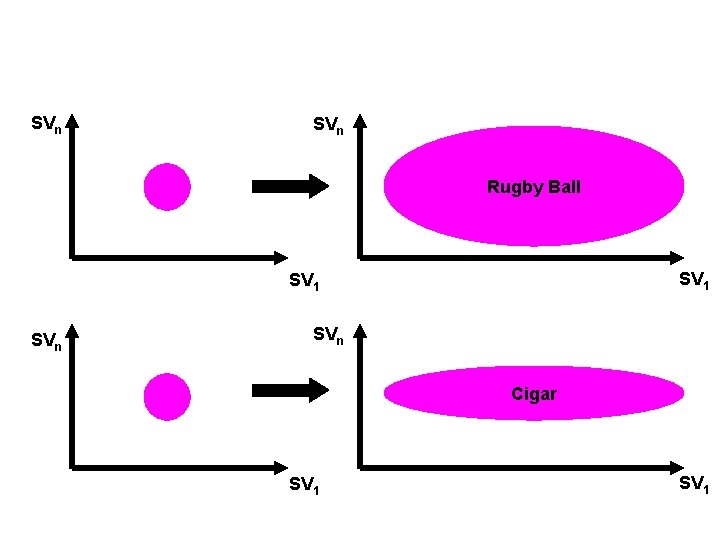
SVn Rugby Ball SV 1 SVn Cigar SV 1

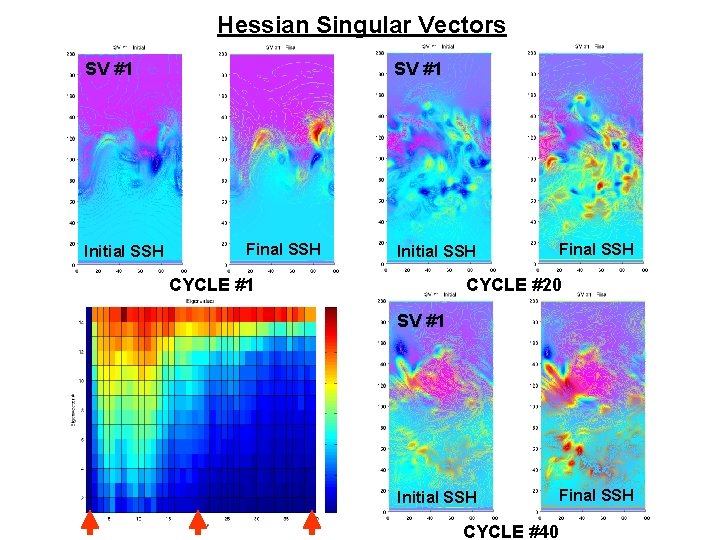
Hessian Singular Vectors SV #1 Initial SSH SV #1 Final SSH Initial SSH CYCLE #1 Final SSH CYCLE #20 SV #1 Initial SSH Final SSH CYCLE #40

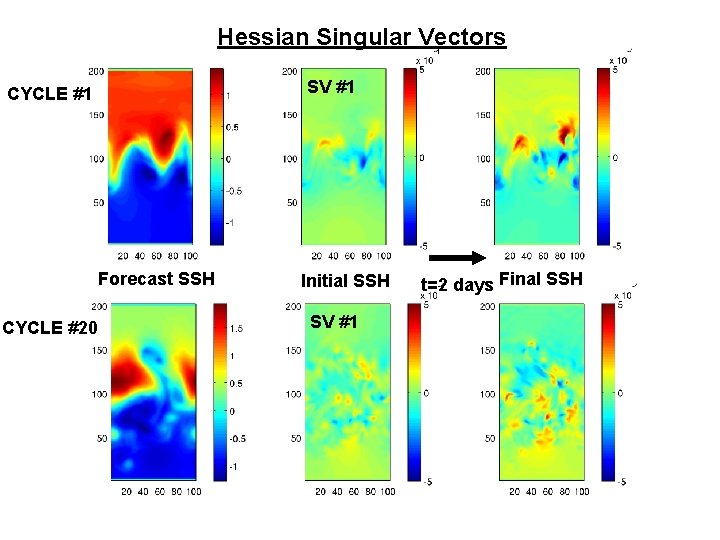
Hessian Singular Vectors SV #1 CYCLE #1 Forecast SSH CYCLE #20 Initial SSH SV #1 t=2 days Final SSH

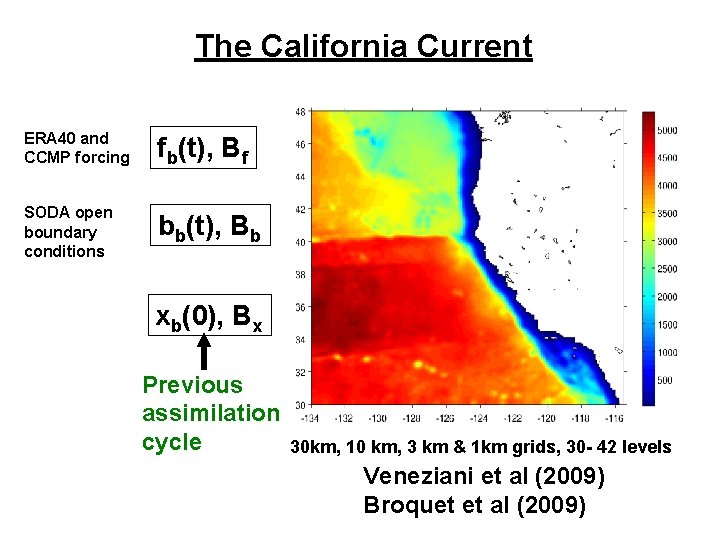
The California Current ERA 40 and CCMP forcing fb(t), Bf SODA open boundary conditions bb(t), Bb xb(0), Bx Previous assimilation cycle 30 km, 10 km, 3 km & 1 km grids, 30 - 42 levels Veneziani et al (2009) Broquet et al (2009)

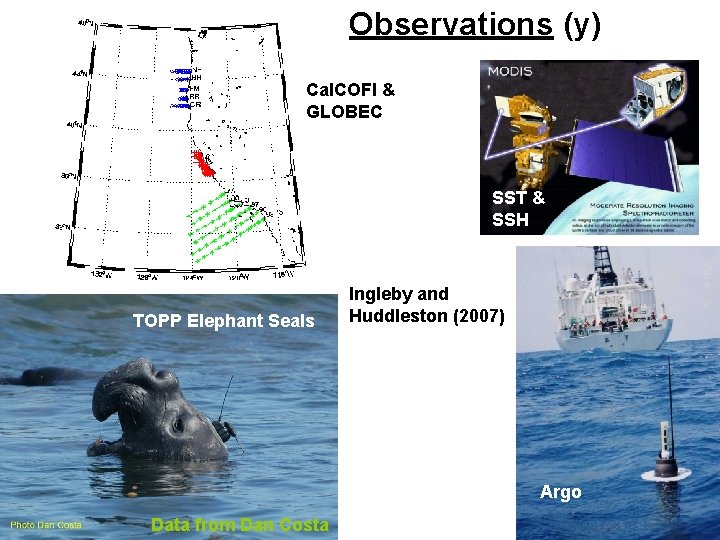
Observations (y) Cal. COFI & GLOBEC SST & SSH TOPP Elephant Seals Ingleby and Huddleston (2007) Argo Data from Dan Costa

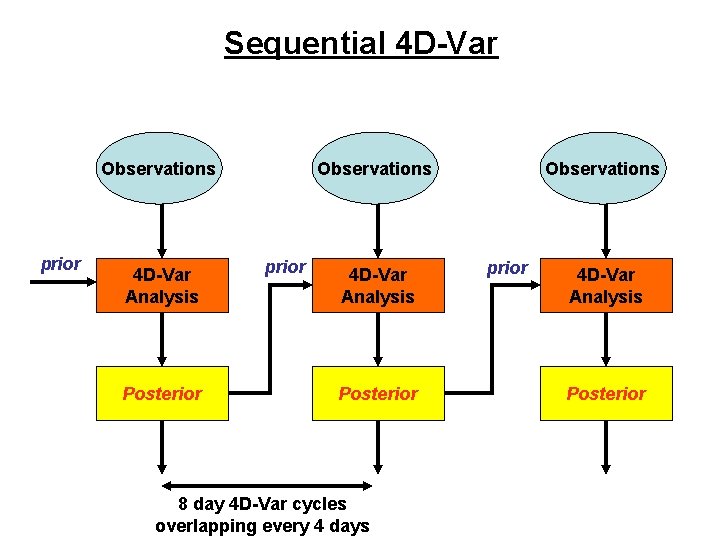
Sequential 4 D-Var Observations prior 4 D-Var Analysis Posterior 8 day 4 D-Var cycles overlapping every 4 days Observations prior 4 D-Var Analysis Posterior

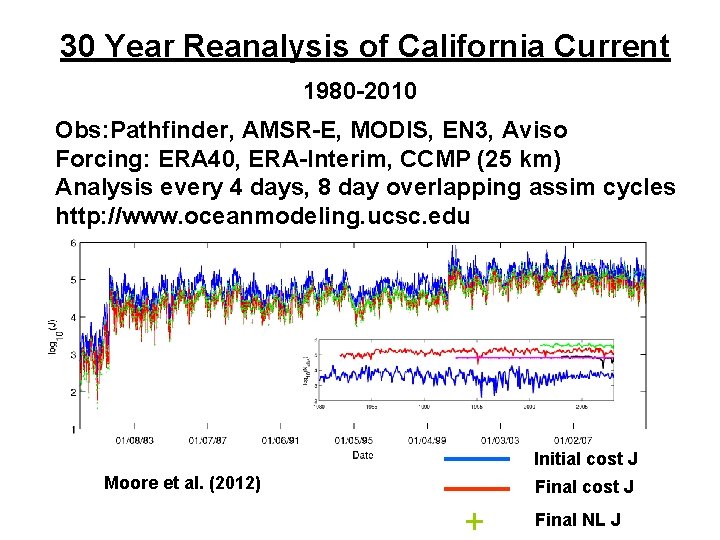
30 Year Reanalysis of California Current 1980 -2010 Obs: Pathfinder, AMSR-E, MODIS, EN 3, Aviso Forcing: ERA 40, ERA-Interim, CCMP (25 km) Analysis every 4 days, 8 day overlapping assim cycles http: //www. oceanmodeling. ucsc. edu Initial cost J Moore et al. (2012) Final cost J + Final NL J

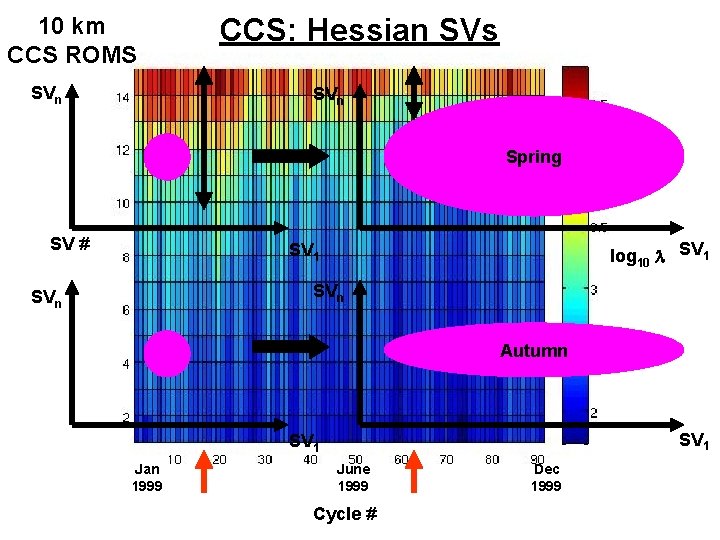
10 km CCS ROMS SVn CCS: Hessian SVs SVn Spring SV # log 10 l SV 1 SVn Autumn SV 1 Jan 1999 June 1999 Cycle # Dec 1999

SVn Spring SV 1 SVn Autumn SV 1

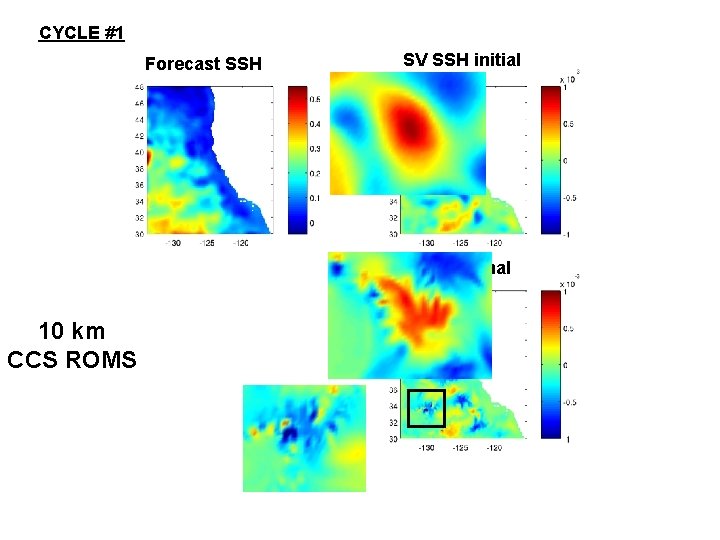
CYCLE #1 Forecast SSH SV SSH initial SV SSH final 10 km CCS ROMS

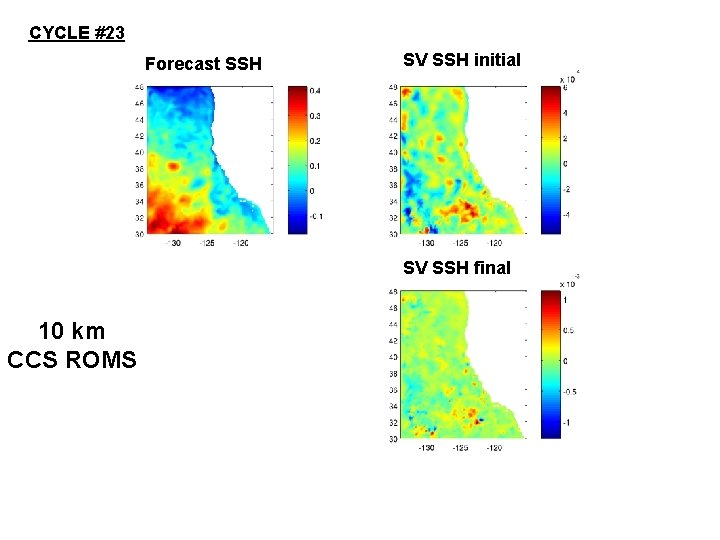
CYCLE #23 Forecast SSH SV SSH initial SV SSH final 10 km CCS ROMS

The Forecast Error Covariance Recall that we can express the forecast error cov. as: Forecast error covariance Tangent linear model Control priors where: Posterior error covariance Tangent Linear 4 D-Var So the control SVD problem becomes: (computational cost equals (# inner-loops)2) Adjoint Linear 4 D-Var

Summary • SVD provides information about forecast error growth. • Growing directions of the forecast error covariance error ellipsoid vary with time • SV structures become smaller scale • Flow and/or error dependent regimes • Future work: - explicit forecast error covariance - model error and weak constraint - control singular vectors