CHARACTERISTICS OF EXPONENTIAL FUNCTIONS A function that can

CHARACTERISTICS OF EXPONENTIAL FUNCTIONS

A function that can be expressed in the form and is positive, is called an Exponential Functions with positive values of x are increasing, one-to-one functions. The parent form of the graph has a y-intercept at (0, 1) and passes through (1, b). The value of b determines the steepness of the curve. The function is neither even nor odd. There is no symmetry. There is no local extrema.

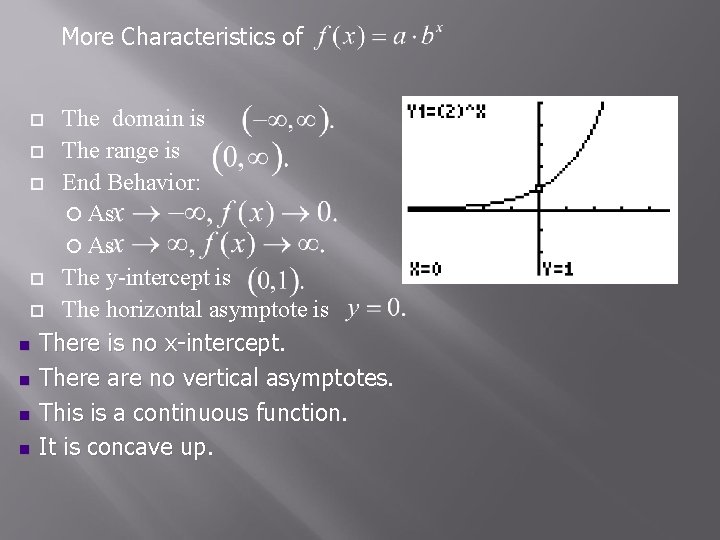
More Characteristics of The domain is The range is End Behavior: As The y-intercept is The horizontal asymptote is n There is no x-intercept. n There are no vertical asymptotes. n This is a continuous function. n It is concave up.

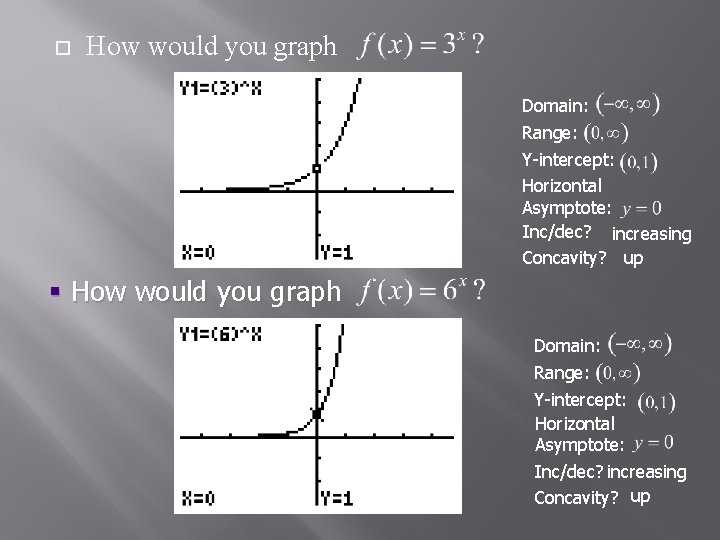
How would you graph Domain: Range: Y-intercept: Horizontal Asymptote: Inc/dec? increasing Concavity? up § How would you graph Domain: Range: Y-intercept: Horizontal Asymptote: Inc/dec? increasing Concavity? up

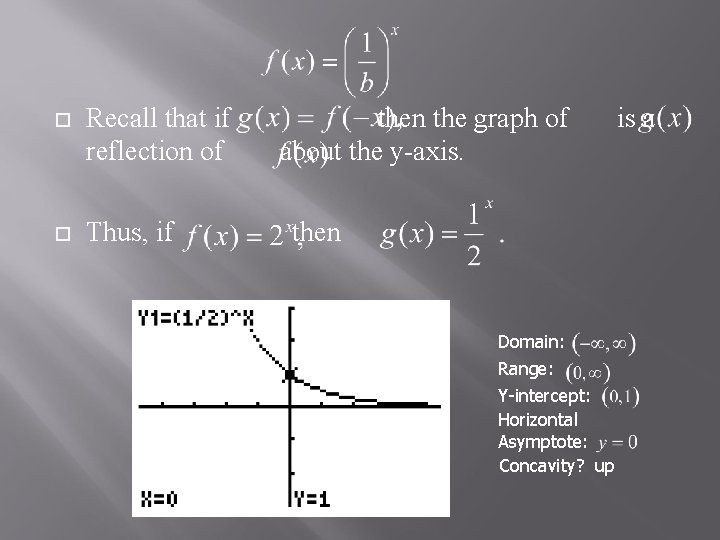
Recall that if reflection of Thus, if then the graph of about the y-axis. then Domain: Range: Y-intercept: Horizontal Asymptote: Concavity? up is a

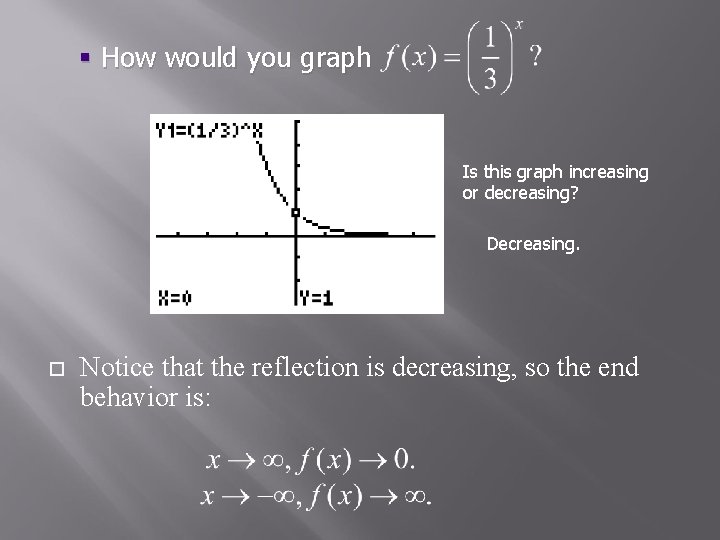
§ How would you graph Is this graph increasing or decreasing? Decreasing. Notice that the reflection is decreasing, so the end behavior is:

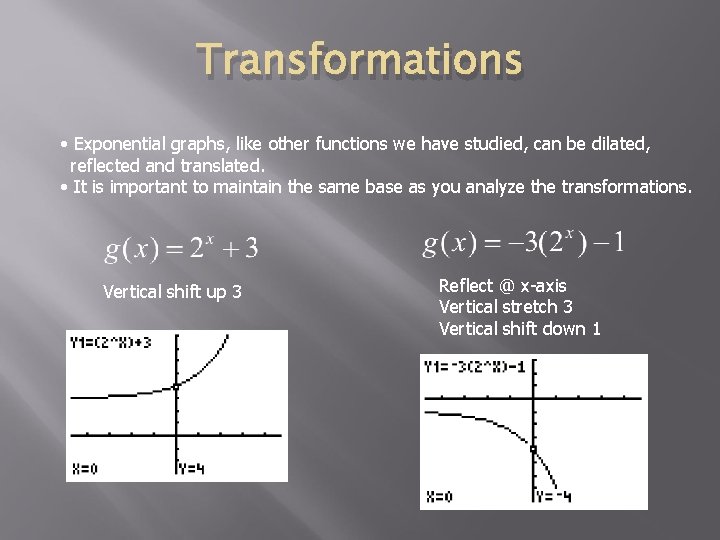
Transformations • Exponential graphs, like other functions we have studied, can be dilated, reflected and translated. • It is important to maintain the same base as you analyze the transformations. Vertical shift up 3 Reflect @ x-axis Vertical stretch 3 Vertical shift down 1

More Transformations Reflect about the x-axis. Horizontal shift right 1. Vertical shift up 1. Vertical shrink ½. Horizontal shift left 2. Domain: Range: Horizontal Asymptote: Y-intercept: Inc/dec? decreasing Concavity? down Domain: Range: Horizontal Asymptote: Y-intercept: Inc/dec? increasing Concavity? up Vertical shift down 3.