ChapterSeventeen Correlation Regression Analysis Product moment correlation is

Chapter_Seventeen Correlation & Regression Analysis Product moment correlation is a statistic is used to summarize the strength of association between two metric (interval or ratio) variables say X and Y. It is also known as Pearson Correlation Co-efficient, Simple Correlation, Bivariate Correlation or simply Correlation Co-efficient. It is proposed by Karl Pearson. Ex: How strongly are sales related to advertising expenditures? Formula: The value of r varies between -1 and +1. The value of r is equal 1. 0 means there is no linear relationship between X and Y 2. 1 means there is a positive strong relationship between X and Y 3. -1 means there is a negative strong relationship between X and Y Naresh K. Malhotra Marketing Research-an applied orientation, 4 th ed.

Regression Analysis Regression analysis is a powerful and flexible procedure for analyzing associative relationships between a metric dependent variable and one or more independent variables. It is concerned with the nature and degree of association between variables and does not imply or assume any causality. It is used in the following ways: 1. Determine whether the independent variables explain a significant variation in the dependent variable: Whether a relationship exists 2. Determine how much of the variation in the dependent variable can be explained by the independent variables: Strength of the relationship 3. Determine the structure or form of the relationship: The mathematical equation relating the independent and dependent variables 4. Predict the values of the dependent variable 5. Construct for other independent variables where evaluating the contributions of a specific variable or set of variables.

Bivariate Regression Bivariate regression is a procedure for deriving a mathematical relationship in the form of an equation between a single metric dependent or criterion variable and a single metric independent or predictor variable. Ex: Can the variation in market share be accounted for by the size of the sales force? Equation:

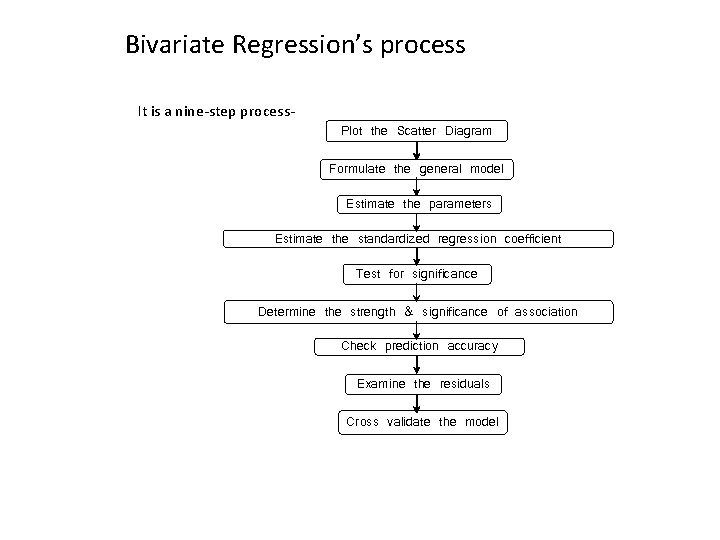
Bivariate Regression’s process It is a nine-step process. Plot the Scatter Diagram Formulate the general model Estimate the parameters Estimate the standardized regression coefficient Test for significance Determine the strength & significance of association Check prediction accuracy Examine the residuals Cross validate the model

Bivariate Regression’s process Step I A scatter diagram or scatter gram is a plot of the values of two variables for all the cases or observations. Simply, it is a form of relationship between the variables. It is used to plot the dependent variable on the vertical axis and the independent variable on the horizontal axis. In the scatter diagram, independent variable is shown in the horizontal axis whereas the dependent variable is shown in the vertical axis. If one variable increases, so does the other, then the relationship is described as linear or a straight line. The most commonly used technique for fitting a straight line to a scatter gram is the least-squares procedure. The technique determines the best-fitting line by minimizing the square of the vertical distances of all the points from the line. The best-fitting line is called the regression line. Any point that does not fall on the regression line is not fully accounted for. The vertical distance from the point to the line is the error,

Bivariate Regression’s process Step II In the Bivariate regression model, the general form of a straight line is: Where, But in marketing research, the basic regression model will be-

Bivariate Regression’s process Step III In the most cases, and are unknown and are estimated from the sample observations using the equation: ; where is the estimated or predicted value of. The value of a and b will be found by the following formula: Number One: Number Two:

Bivariate Regression’s process Step IV Standardization is the process by which the raw data are transformed into new variables that have a mean of 0 and a variance of 1. When the data are standardized, the intercept assumes a value of 0. The term beta coefficient or beta weight is used to denote the standardized regression coefficient is Step V The statistical significance of the linear relationship between X and Y may be tested by examining the hypotheses: The null hypothesis implies that there is no linear relationship between X and Y. The alternative hypothesis is that there is a relationship-positive or negative between X and Y. Typically, a two-tailed test is done. A t statistic with n – 2 degrees of freedom can be used where-

Bivariate Regression’s process Step V denotes the standard deviation of b and is called the standard error. When the calculated value of t is larger than the critical value, then the null hypothesis is rejected means that there is a significant linear relationship between dependent & independent variable. Step VI Here the strength of association is measured by the coefficient of determination, r 2. In Bivariate regression, r 2 is the square of the simple correlation coefficient obtained by correlating the two variables. The coefficient, r 2 varies between 0 and 1. The value of r 2 is calculated by-

Bivariate Regression’s process Step VI Where, Another equivalent test for examining the significance of the linear relationship between X and Y is the test for the significance of the coefficient of determination. The hypothesis is- Here F statistic is used as (c – 1) and (n – c) is compared with the calculated value. If the calculated value is larger than the critical value then null hypothesis is rejected meaning that there is a significant relationship between dependent and independent variable.

Bivariate Regression’s process Step VII To estimate the accuracy of predicted values, standard error of estimate, , it is useful to calculate the Two cases of prediction may arise. The researcher may want to predict the mean value of y for all the cases with a given value of X, say or predict the value of Y for a single case. Here predicted value is Step VIII Latter Step IX Latter

Multiple Regression Multiple regression involves a single dependent variable and two or more independent variables. Ex: Can variation in sales be explained in terms of variation in advertising expenditures, prices and level of distribution? The general form of the multiple regression model: which is estimated by the following equation:

Multiple Regression Process The steps involved in conducting multiple regression analysis are similar to those for bivariate regression analysis. The discussion focuses on. Partial Coefficients Regression The interpretation of the partial regression coefficient, is that it represents the expected change in Y when is changed by one unit but is held constant or otherwise controlled. Likewise, represents the expected change in Y for a unit change in when is held constant. Thus calling and , partial regression coefficients is appropriate. In other words, if and are each changed by one unit, the expected change in Y would be. Multiple regression can not be solved if 1. Sample size, n is smaller than or equal to the number of independent variables, k 2. One independent variable is perfectly correlated with another

Multiple Regression Process Strength association of The strength of association is measured by the square of the multiple correlation coefficient, which is also called the coefficient of multiple determination, where. The multiple correlation coefficient, R, can also be viewed as the simple correlation coefficient, r, between Y and. Several characteristics of are 1. The coefficient of multiple determination, cannot be less than the highest Bivariate, r 2, of any individual independent variable with the dependent variable. 2. will be larger when the correlations between the independent variables are low 3. If the independent variables are statistically independent (uncorrelated), then will be the sum of Bivariate r 2 of each independent variable with the dependent variable. 4. cannot decrease as more independent variables are added to the regression equation.

Multiple Regression Process Step IX Examination of residual A residual is the difference between the observed value of and the value predicted by the regression equation, . Plotting the residuals against the independent variables provide evidence of the appropriateness or inappropriateness of using a linear model. Again, the plot should result in a random pattern. The residuals should fall randomly with relatively equal distribution dispersion about 0. They should not display any tendency to be either positive or negative.

Multiple Regression Process Step X Significance testing In testing the significance of the overall regression equation as well as specific partial regression coefficients. The null hypothesis for the overall test is that the coefficient of multiple determination in the population, is zero. . This is equivalent to the following null hypothesis: The overall test can be conducted by using an F statistic where-