Chapters 2 4 Proofs practice Chapter 2 Proofs

Chapters 2 – 4 Proofs practice

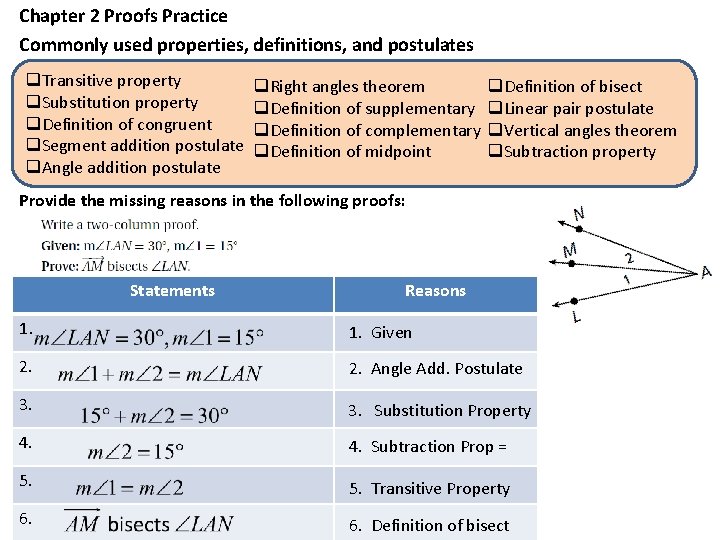
Chapter 2 Proofs Practice Commonly used properties, definitions, and postulates q. Transitive property q. Substitution property q. Definition of congruent q. Segment addition postulate q. Angle addition postulate q. Right angles theorem q. Definition of supplementary q. Definition of complementary q. Definition of midpoint q. Definition of bisect q. Linear pair postulate q. Vertical angles theorem q. Subtraction property Provide the missing reasons in the following proofs: Statements Reasons 1. Given 2. Angle Add. Postulate 3. Substitution Property 4. Subtraction Prop = 5. Transitive Property 6. Definition of bisect

q. Reflexive property q. Transitive property q. Substitution property q. Definition of congruent q. Segment addition postulate q. Angle addition postulate q. Right angles theorem q. Definition of supplementary q. Definition of complementary q. Definition of midpoint q. Definition of bisect q. Linear pair postulate q. Vertical angles theorem q. Subtraction property Given: 1 and 2 are supplementary, and 1 3 Prove: 3 and 2 are supplementary. Statements Reasons 1. Given 2. Definition of Supplementary 3. Definition of . 4. Substitution Property 5. Definition of supplementary

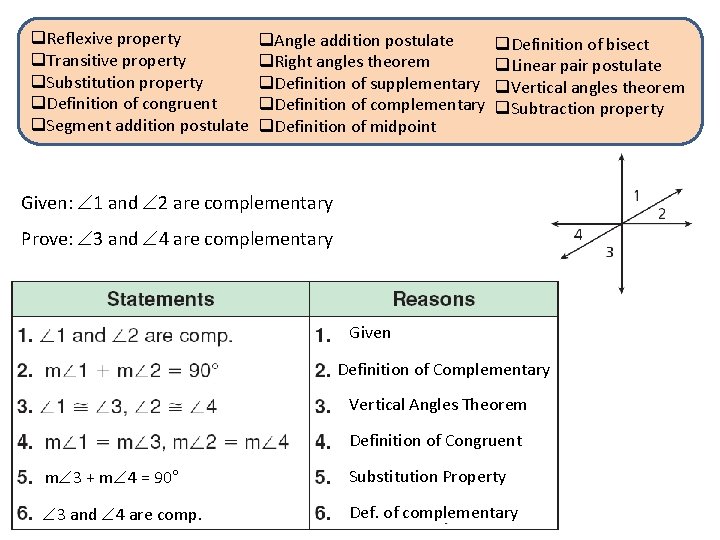
q. Reflexive property q. Transitive property q. Substitution property q. Definition of congruent q. Segment addition postulate q. Angle addition postulate q. Right angles theorem q. Definition of supplementary q. Definition of complementary q. Definition of midpoint q. Definition of bisect q. Linear pair postulate q. Vertical angles theorem q. Subtraction property Given: 1 and 2 are complementary Prove: 3 and 4 are complementary Given Definition of Complementary Vertical Angles Theorem Definition of Congruent m 3 + m 4 = 90° Substitution Property 3 and 4 are comp. Def. of complementary

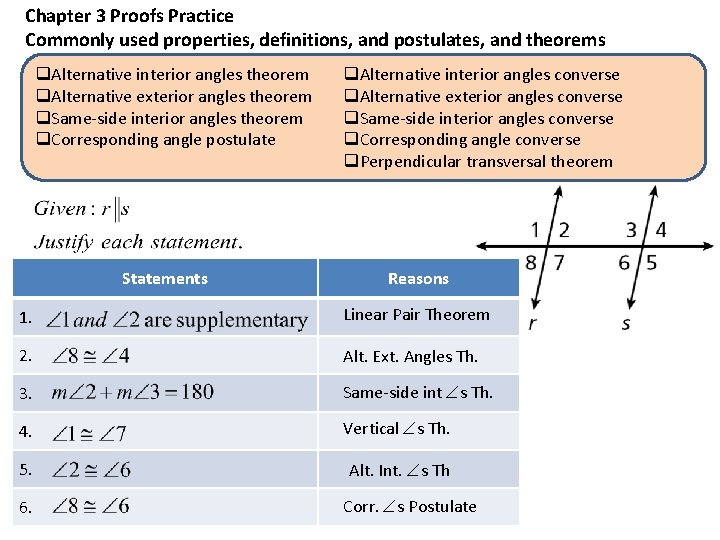
Chapter 3 Proofs Practice Commonly used properties, definitions, and postulates, and theorems q. Alternative interior angles theorem q. Alternative exterior angles theorem q. Same-side interior angles theorem q. Corresponding angle postulate Statements q. Alternative interior angles converse q. Alternative exterior angles converse q. Same-side interior angles converse q. Corresponding angle converse q. Perpendicular transversal theorem Reasons 1. Linear Pair Theorem 2. Alt. Ext. Angles Th. 3. Same-side int s Th. 4. Vertical s Th. 5. Alt. Int. s Th 6. Corr. s Postulate

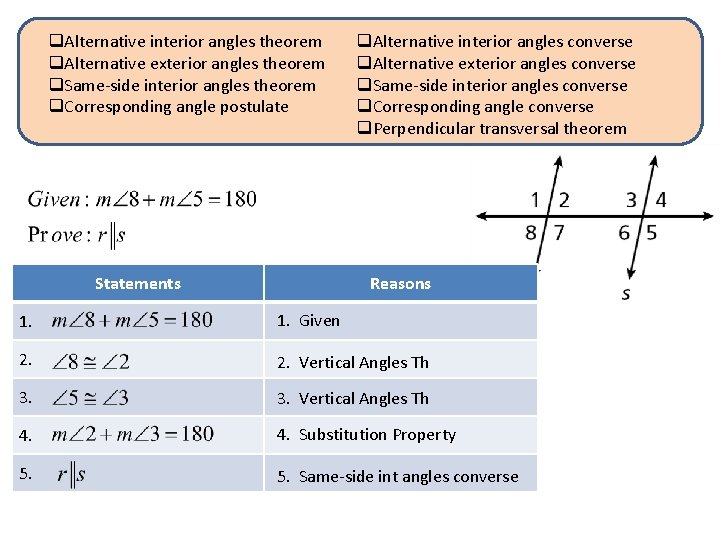
q. Alternative interior angles theorem q. Alternative exterior angles theorem q. Same-side interior angles theorem q. Corresponding angle postulate Statements q. Alternative interior angles converse q. Alternative exterior angles converse q. Same-side interior angles converse q. Corresponding angle converse q. Perpendicular transversal theorem Reasons 1. Given 2. Vertical Angles Th 3. Vertical Angles Th 4. Substitution Property 5. Same-side int angles converse

Chapter 4 Proofs Practice Commonly used properties, definitions, and postulates, and theorems q. Triangle sum theorem q. Exterior angles theorem q. Isosceles triangle converse q. Definition of congruent triangles (CPCTC) q. SSS q. SAS q. ASA q. AAS q. HL Statements Reasons 1. Given 2. Given 3. All rt s are congruent 4. Def. of Midpoint 5. Vertical Angles theorem 6. ASA

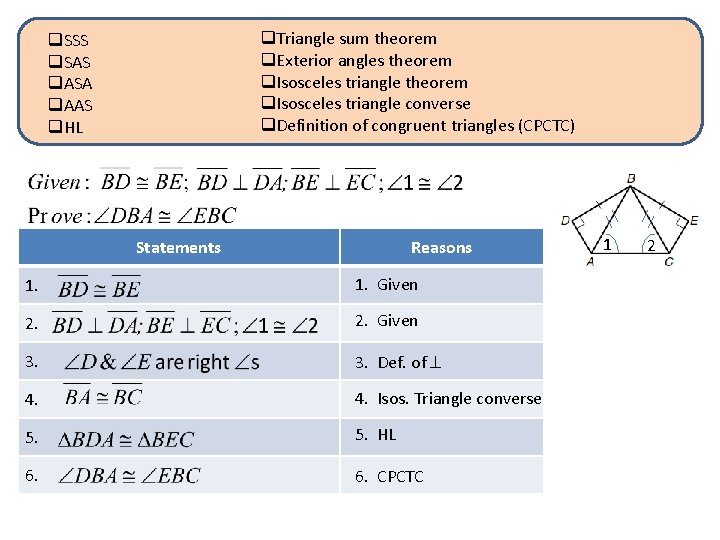
q. Triangle sum theorem q. Exterior angles theorem q. Isosceles triangle converse q. Definition of congruent triangles (CPCTC) q. SSS q. SAS q. ASA q. AAS q. HL Statements Reasons 1. Given 2. Given 3. Def. of 4. Isos. Triangle converse 5. HL 6. CPCTC 1 2

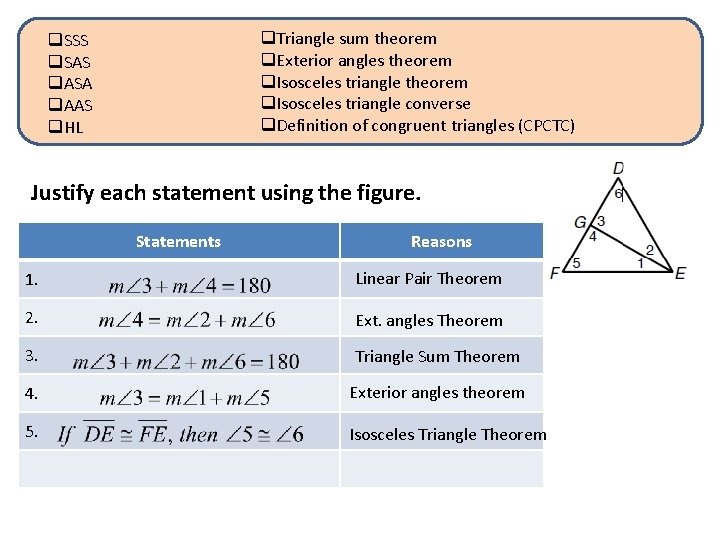
q. Triangle sum theorem q. Exterior angles theorem q. Isosceles triangle converse q. Definition of congruent triangles (CPCTC) q. SSS q. SAS q. ASA q. AAS q. HL Justify each statement using the figure. Statements Reasons 1. Linear Pair Theorem 2. Ext. angles Theorem 3. Triangle Sum Theorem 4. Exterior angles theorem 5. Isosceles Triangle Theorem