Chapters 10 Chemical Quantities Conversion Factors n Conversion

Chapters 10 Chemical Quantities

Conversion Factors n Conversion factor – A fraction equal to 1 that is used to change one unit into another. (When the numerator = denominator, a fraction equals 1. )

Dimensional Analysis n Dimensional Analysis – A problem solving method where conversion factors are used to cancel unwanted units.

Conversion Examples a) Convert $25 to nickels. $25 4 quarters 5 nickels $1 1 quarter 25 * 4 * 5 / 1 = 500 nickels

Conversion Example 2 n Convert 180 days to seconds. 180 days 24 hours 1 day 60 minutes 60 seconds 1 hour 1 minute 180 * 24 * 60 / 1 / 1 = 15, 552, 000 seconds or 1. 6 x 107 seconds

Common Conversions to Know 1 meter = 100 centimeters 1 meter = 1000 millimeters 1 kilometer = 1000 meters Convert 125 cm to km. 1 m 1 km 125 cm n 100 cm 1000 m 125 / 1000 = 0. 00125 km or 1. 25 x 10 -3 km

Conversion Example 4 n Convert 15 m/s to km/hr. 15 m 1 s 1 km 60 seconds 60 minutes 1000 m 1 minute 1 hour 15 * 60 / 1000 = 54 km/hr

Measuring Matter n How do we describe how much of something we have? n By count, by mass, by volume. n We use words like “dozen” to talk about an amount. n In chemistry, we use the MOLE.

Mole n Mole – SI unit for measuring an amount of a substance. 1 mole = 6. 02 x 1023 representative particles n Avogadro’s Number = 6. 02 x 1023 n Representative particles = smallest unit that still has all the characteristics of that substance.

Representative Particles n What is the representative particle of : • atom Element (ex. Cu): ______ Exception: The representative particle of the 7 diatomic elements is a molecule. (ex. H 2) • molecule Covalent compound (ex. H 2 O): _____ • formula unit Ionic Compound (ex. Na. Cl): ______

Conversions n 4 moles Ca = 4 moles Ca atoms Ca. 6. 02 x 1023 atoms Ca 1 mole Ca = 2. 41 x 1024 atoms Ca

Conversions n 5 x 1018 atoms Cu = 5 x 1018 atoms Cu moles Cu. 1 mole Cu 6. 02 x 1023 atoms Cu = 8. 3 x 10 -6 moles Cu

Conversions n 9. 2 moles F 2 = 9. 2 moles molecules F 2? 6. 02 x 1023 molecules F 2 1 mole = 5. 5 x 1024 molecules F 2

Conversions n 9. 2 moles F 2 = 9. 2 moles F 2 atoms F? 6. 02 x 1023 mlcls F 2 2 atoms F 1 molecule F 2 = 1. 1 x 1025 atoms F

Conversions n 3. 4 moles C 2 H 4 = total atoms? 3. 4 moles C 2 H 4 6. 02 x 1023 mlcls C 2 H 4 6 atoms 1 mole C 2 H 4 1 mlcl C 2 H 4 = 1. 22 x 1025 atoms

Molar Mass n Molar Mass – The mass of one mole of an element or compound. n Molar mass of a compound = the sum of the masses of the atoms in the formula. n Use the atomic masses in grams/mol on the periodic table.

Molar Mass n Find the molar mass of each: n Sr 87. 6 g/mol n Mg. Br 2 (24. 3) + (2 x 79. 9) = 184. 1 g/mol n Ba 3(PO 4)2 (3 x 137. 38) + (2 x 30. 97) + (8 x 16) = 602. 1 g/mol

Mole–Gram Conversions 1 mole = molar mass (in grams) 5. 3 moles Li. OH = ______ grams Li. OH (Molar mass Li. OH : 7 + 16 + 1 = 24 g/mol) 5. 3 moles Li. OH 24 g Li. OH 1 mole Li. OH = 127. 2 grams Li. OH

Gram-Mole Conversions n 68 grams F 2 = 68 grams F 2 moles F 2? 1 mole F 2 38 grams 68 / 38 = 1. 8 moles F 2

STP n STP = Standard Temperature & Pressure Standard Temp 0 o. C n Standard Press 1 atm n (See Reference Tables)

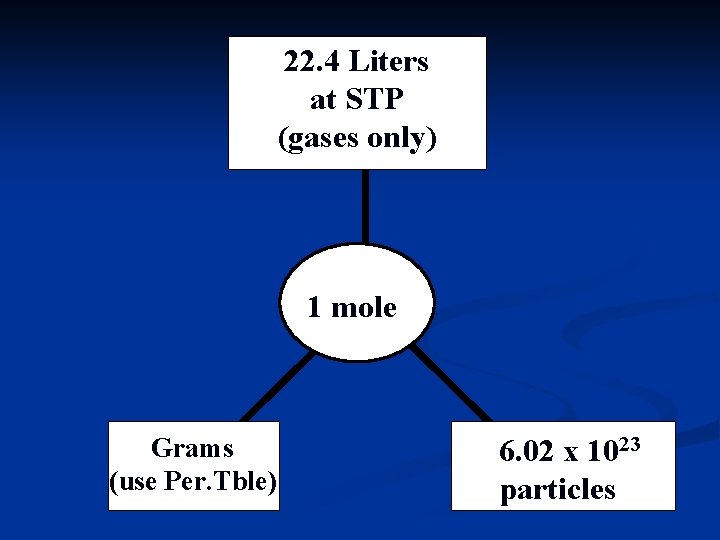
Molar Volume of a Gas n Avogadro’s Hypothesis: equal volumes of gases at the same temperature and pressure contain equal numbers of particles. n At STP, 1 mole of any gas occupies a volume of 22. 4 L. 1 mole = 22. 4 L (of a gas at STP)

Mole-Volume Conversions n 5. 4 moles He = 5. 4 moles He L He at STP? 22. 4 L He 1 mole He 5. 4 x 22. 4 = 120. 96 L He

Mole-Volume Conversions n 5. 4 moles CH 4 = 5. 4 moles CH 4 L CH 4 gas at STP? 22. 4 L CH 4 1 mole CH 4 5. 4 x 22. 4 = 120. 96 L CH 4

Volume-Mole Conversion n 560 L SO 3 = 560 L SO 3 mol SO 3 at STP 1 mole SO 3 22. 4 L SO 3 560 / 22. 4 = 25 mole SO 3

Molar Mass-Density Conversions Density = grams liters Molar Mass = grams mole A gaseous compound composed of sulfur and oxygen has a density of 3. 58 g/L at STP. What is the molar mass of this gas? 3. 58 g L 22. 4 L 1 mole 3. 58 x 22. 4 = 80. 2 g/mole

Molar Mass-Density Conversion n What is the density of Krypton gas at STP? 83. 8 grams Kr mole 1 mole 22. 4 Liters 83. 8 / 22. 4 = 3. 74 g/L Kr

22. 4 Liters at STP (gases only) 1 mole Molar Mass Grams (use Per. Tble) 6. 02 x 1023 particles 23 6. 02 x 10 particles

Multi-step Problem: Example 1 If you had 5. 0 L of CO 2 how many grams would that be? n Step 1: L moles n Step 2: moles grams n 5. 0 L CO 2 1 mole CO 2 22. 4 L CO 2 44. 0 g CO 29. 8 = g CO 2 1 mole CO 2

Multi-step Problem: Example 2 How many molecules are in 60. 0 grams of water? n Step 1: grams moles n Step 2: moles molecules n 60. 0 g H 2 O 1 mole H 2 O 6. 02 x 1023 mlcls = 18. 0 g H 2 O 1 mole H 2 O = 2. 0 x 1024 molecules of H 2 O

Percent Composition n Percent Composition - % by mass of each element in a compound Part x 100 n Percent = Whole

Percent Composition Percent Comp = Mass of 1 element x 100 Mass of compound n Example: Find the mass percent composition of Al 2(SO 4)3 n Al: 2 x 27 = 54 S: 3 x 32 = 96 O: 12 x 16 = 192 Total Comp. = 342 54 x 100 = 15. 8% % Al: 342 % S: 96 x 100 = 28. 1% 342 %O: 192 x 100 = 56. 1% 342

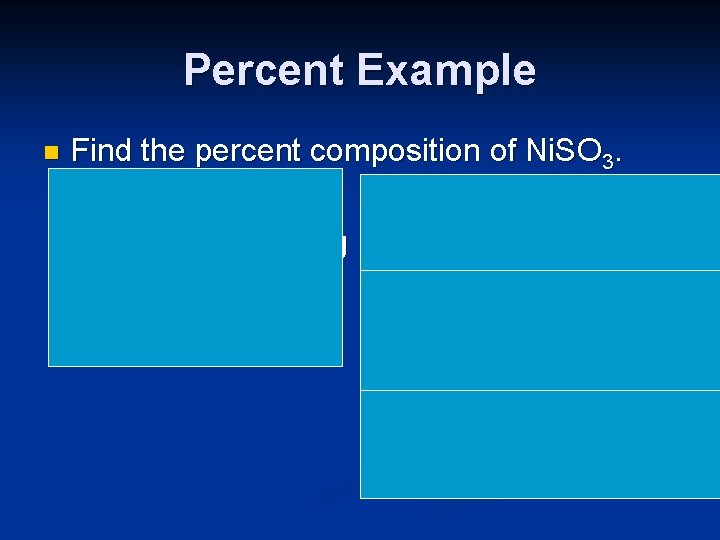
Percent Example n Find the percent composition of Ni. SO 3. Ni: 58. 7 g %Ni: 58. 7 x 100 = 42. 3 % S: 32 g 138. 7 O: (3 x 16) = 48 g %S: 32 x 100 = 23. 1 % 138. 7 Total Comp. 138. 7 %O: 48 x 100 = 34. 6% 138. 7

More Percents n Which of the following shows a compound that is 92. 3%C and 7. 7%H? a) C 2 H 4 c) CH 4 b) C 3 H 6 d) C 6 H 6

Empirical Formulas n Empirical Formula – The simplest formula. n n Shows the smallest whole number ratio of elements in a compound. Covalent formulas will not always be empirical. Example: CH Molecular Formula – The actual formula. n n n For ionic compounds – it will be the simplest ratio. For molecular compounds – it will NOT always be the simplest ratio. Example: C 6 H 6

To Calculate Empirical Formula n Calculate the empirical formula of a 2. 5 gram compound containing 0. 90 g Ca and 1. 60 g Cl. n Step 1: Convert GRAMS to MOLES. n Ca: n Cl: 0. 90 g 1. 60 g 1 mole 40. 1 g = 0. 0224 mole Ca 1 mole 35. 5 g = 0. 0451 mole Cl

Calculating Empirical Formula n Step 2: DIVIDE the # of moles of each substance by the smallest number to get the simplest mole ratio. Ca: 0. 0224 = 1 0. 0224 Ca. Cl 2 Cl: 0. 0451 = 2. 01 ~ 2 0. 0224

Calculating Empirical Formulas Step 3: If the numbers are whole numbers, use these as the subscripts for the formula. If the numbers are not whole numbers, multiply each by a factor that will make them whole numbers. n Look for these fractions: n 0. 5 x 2 n 0. 33 x 3 n 0. 25 x 4 n

Empirical Formula Example n What is the empirical formula of a compound that is 66% Ca and 34% P? (Assume you have 100 grams of a compound and replace % with grams. )

Empirical Formula Example n Step 1: grams moles Ca: 66 g P n 1 mole = 1. 646 mole Ca 40. 1 g 34 g 1 mole = 1. 097 mole P 31. 0 g Step 2: Divide by the smallest. Ca: 1. 646 = 1. 5 1. 097 P: 1. 097 = 1 1. 097

Empirical Formula Example n Step 3: Multiply until you get whole numbers. (If you multiply one factor by a number, you have to multiply ALL the factors by that number!) Ca: 1. 5 x 2 = 3 P: 1 x 2 = 2 Ca 3 P 2

Determining Molecular Formulas n A compound has an empirical formula of CH 2 O. Its molecular mass is 180 g/mol. What is its molecular formula? n Step 1: Find the mass of the empirical formula. C: 1 x 12 = 12 H: 2 x 1 = 2 O: 1 x 16 = 16 Total: 30

Determining Molecular Formula n Step 2: Divide the molecular mass by the mass of the empirical formula to get the “multiplying factor”. 180 =6 30 n Step 3: Multiply each of the subscripts in the empirical formula by this factor to get the molecular formula. 6 (CH 2 O) C 6 H 12 O 6

Determining Molecular Formula Find the molecular formula of ethylene glycol (CH 3 O) if its molar mass is 62 g/mol. Step 1: 12 + (3 x 1) + 16 = 31 g/mol Step 2: 62 / 31 = 2 Step 3: 2 (CH 3 O) C 2 H 6 O 2

Empirical/Molecular Example n The percent composition of methyl butanoate is 58. 8% C, 9. 8% H, and 31. 4 % O and its molar mass is 204 g/mol. n What is its empirical formula? n What is its molecular formula?

Empirical/Molecular Example 58. 8 g C 1 mol C 12. 0 g C = 4. 9 mol C 4. 9 = 2. 5 x 2 = 5 1. 96 9. 8 g H 1 mol H 1. 0 g H = 9. 8 mol H 9. 8 = 5 1. 96 x 2 = 10 31. 4 g O 1 mol O 16. 0 g O = 1. 96 mol O 1. 96 = 1 1. 96 x 2=2 Empirical Formula = C 5 H 10 O 2

Empirical/Molecular Example Empirical Formula C 5 H 10 O 2 Mass = 5(12) + 10(1) + 2(16) = 102 g/mole Molecular mass 204 g/mol = 2 Empirical mass 102 g/mol So molecular formula is 2 x emp. form: 2(C 5 H 10 O 2) = C 10 H 20 O 4