Chapters 10 11 Rotation and angular momentum Rotation

Chapters 10, 11 Rotation and angular momentum

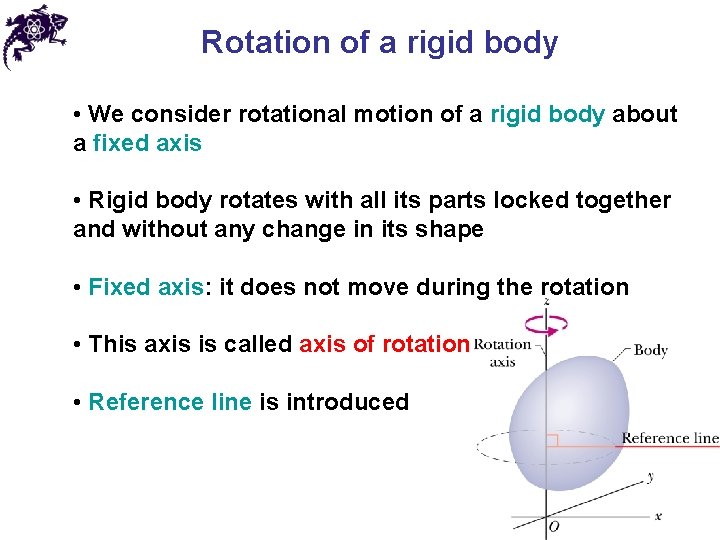
Rotation of a rigid body • We consider rotational motion of a rigid body about a fixed axis • Rigid body rotates with all its parts locked together and without any change in its shape • Fixed axis: it does not move during the rotation • This axis is called axis of rotation • Reference line is introduced

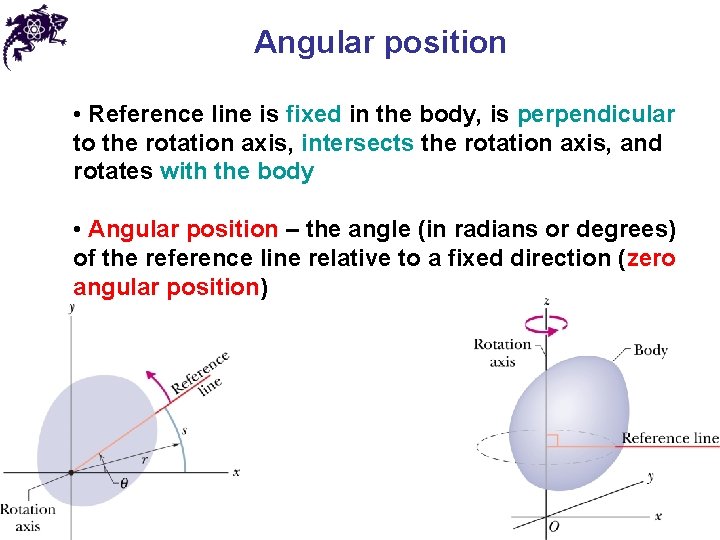
Angular position • Reference line is fixed in the body, is perpendicular to the rotation axis, intersects the rotation axis, and rotates with the body • Angular position – the angle (in radians or degrees) of the reference line relative to a fixed direction (zero angular position)

Angular displacement • Angular displacement – the change in angular position. • Angular displacement is considered positive in the CCW direction and holds for the rigid body as a whole and every part within that body

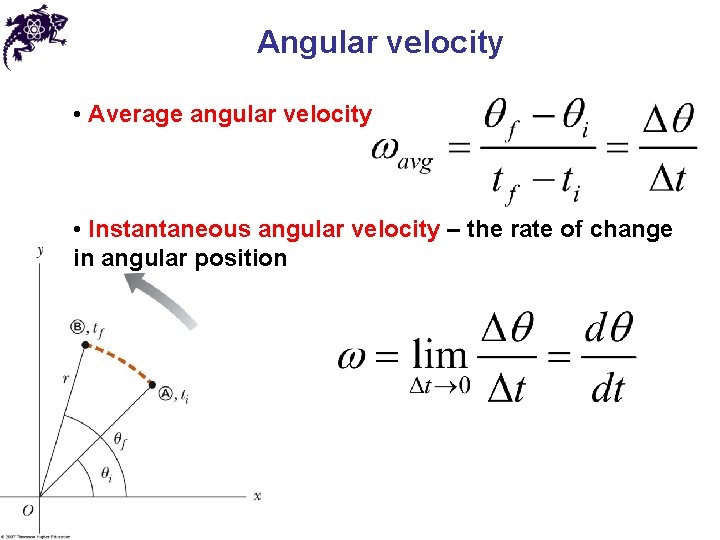
Angular velocity • Average angular velocity • Instantaneous angular velocity – the rate of change in angular position

Angular acceleration • Average angular acceleration • Instantaneous angular acceleration – the rate of change in angular velocity

Rotation with constant angular acceleration • Similarly to the case of 1 D motion with a constant acceleration we can derive a set of formulas:

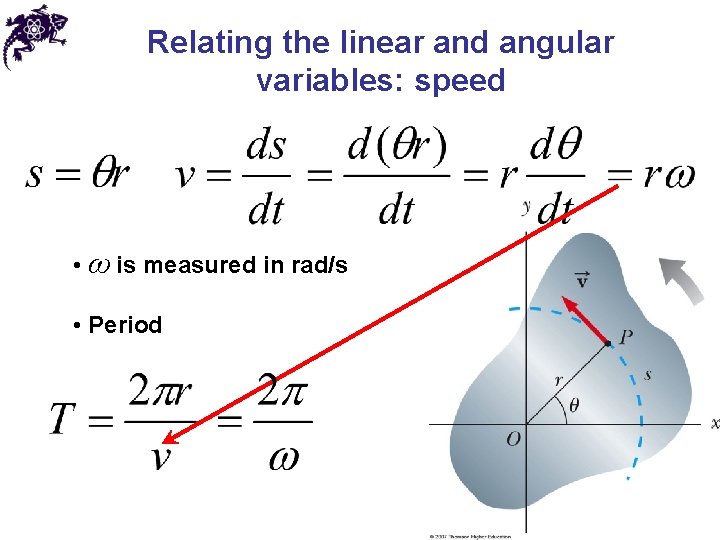
Relating the linear and angular variables: position • For a point on a reference line at a distance r from the rotation axis: • θ is measured in radians

Relating the linear and angular variables: speed • ω is measured in rad/s • Period

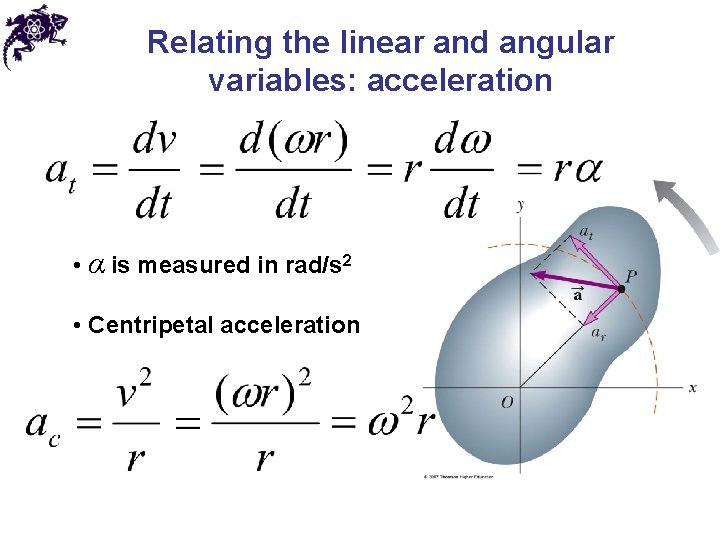
Relating the linear and angular variables: acceleration • α is measured in rad/s 2 • Centripetal acceleration

Rotational kinetic energy • We consider a system of particles participating in rotational motion • Kinetic energy of this system is • Then

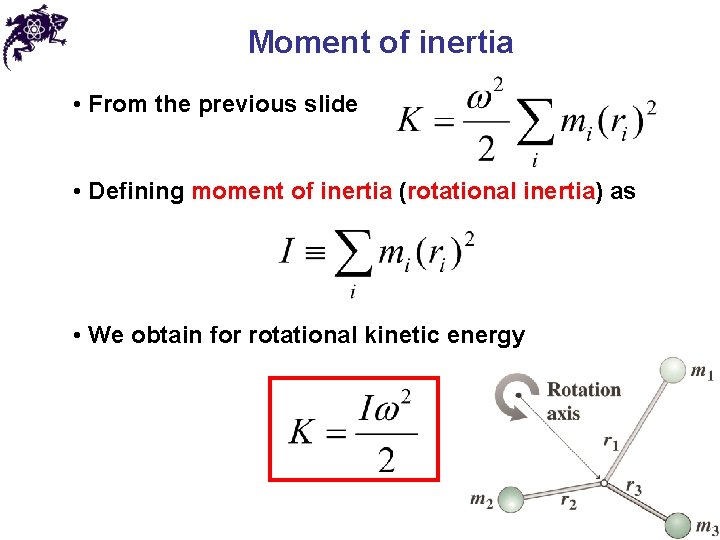
Moment of inertia • From the previous slide • Defining moment of inertia (rotational inertia) as • We obtain for rotational kinetic energy

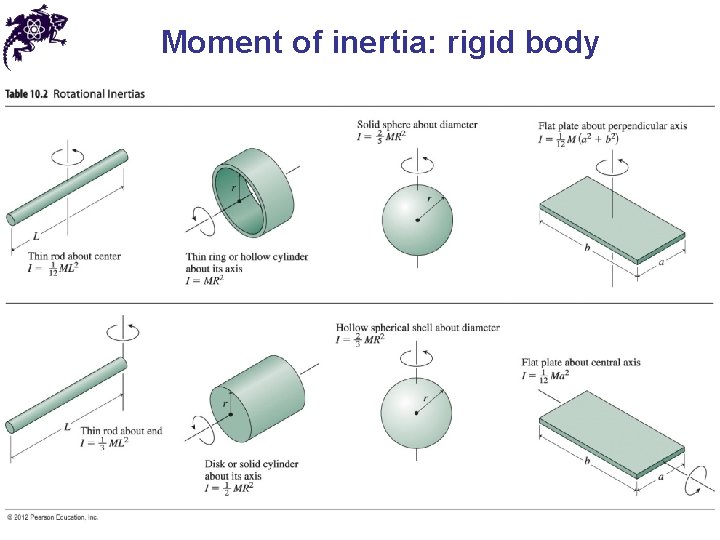
Moment of inertia: rigid body • For a rigid body with volume V and density ρ(V) we generalize the definition of a rotational inertia: • This integral can be calculated for different shapes and density distributions • For a constant density and the rotation axis going through the center of mass the rotational inertia for 8 common body shapes is given in Table 10 -2 (next slide)

Moment of inertia: rigid body

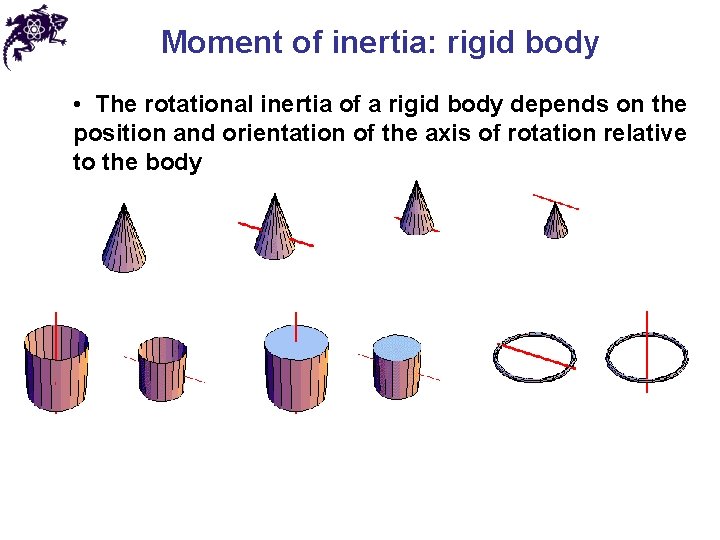
Moment of inertia: rigid body • The rotational inertia of a rigid body depends on the position and orientation of the axis of rotation relative to the body

Chapter 10 Problem 25 Four equal masses m are located at the corners of a square of side L, connected by essentially massless rods. Find the rotational inertia of this system about an axis (a) that coincides with one side and (b) that bisects two opposite sides.

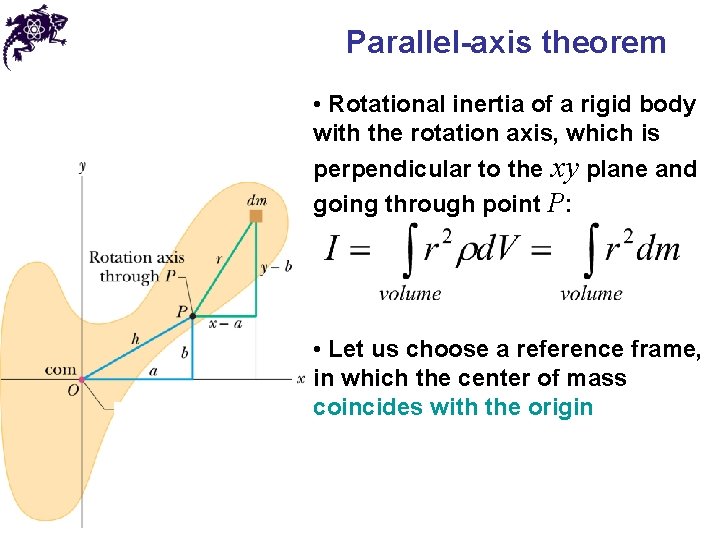
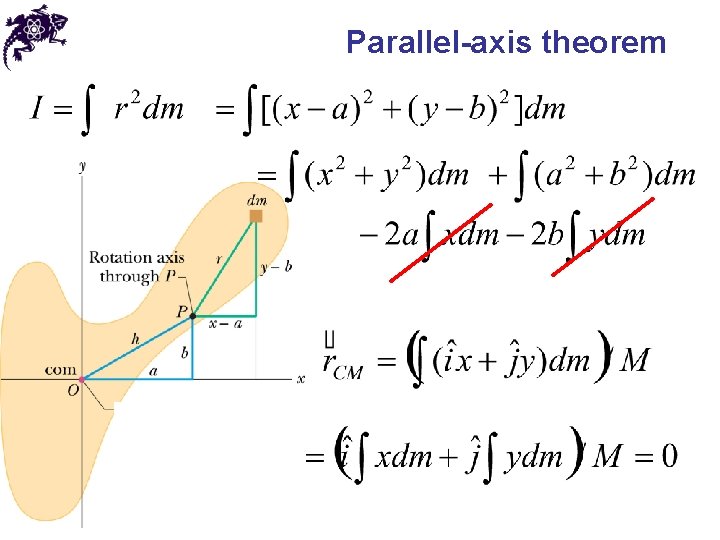
Parallel-axis theorem • Rotational inertia of a rigid body with the rotation axis, which is perpendicular to the xy plane and going through point P: • Let us choose a reference frame, in which the center of mass coincides with the origin

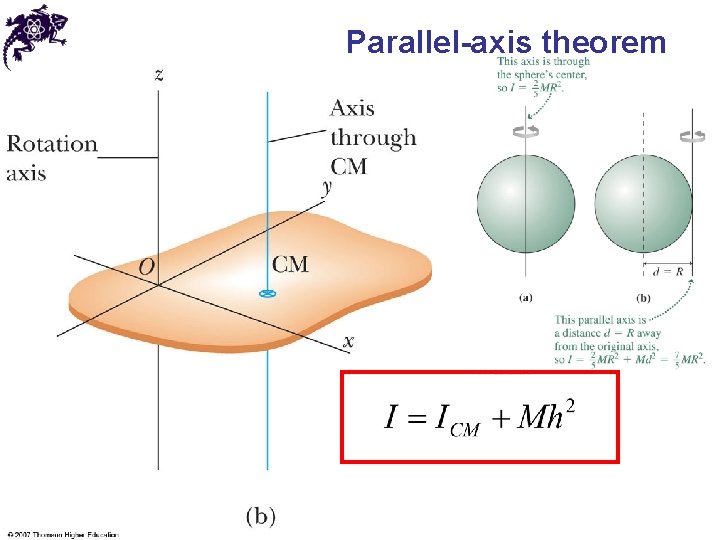
Parallel-axis theorem

Parallel-axis theorem R

Parallel-axis theorem

Chapter 10 Problem 51 A uniform rectangular flat plate has mass M and dimensions a by b. Use the parallel-axis theorem in conjunction with Table 10. 2 to show that its rotational inertia about the side of length b is Ma 2/3.

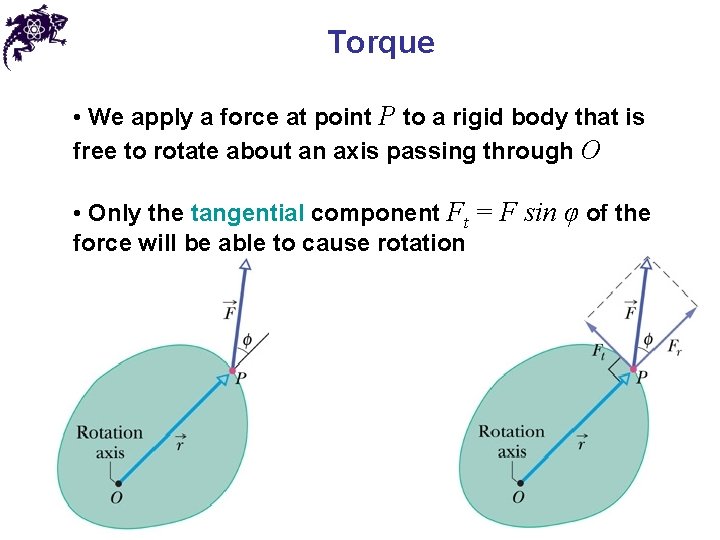
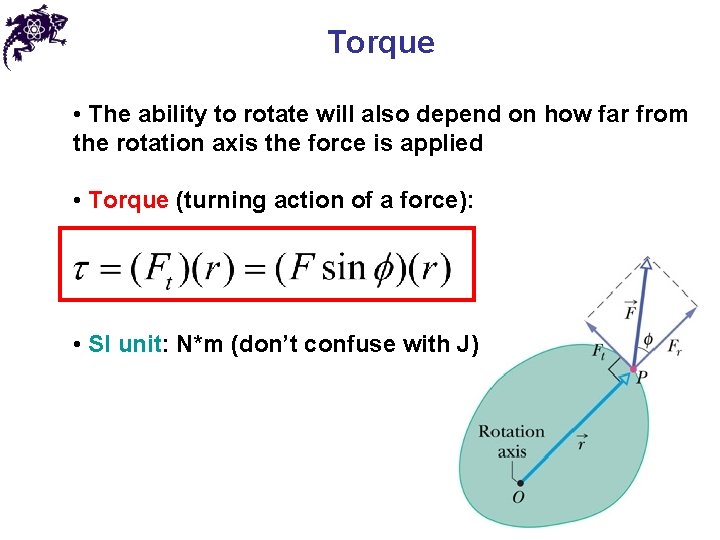
Torque • We apply a force at point P to a rigid body that is free to rotate about an axis passing through O • Only the tangential component Ft = F sin φ of the force will be able to cause rotation

Torque • The ability to rotate will also depend on how far from the rotation axis the force is applied • Torque (turning action of a force): • SI unit: N*m (don’t confuse with J)

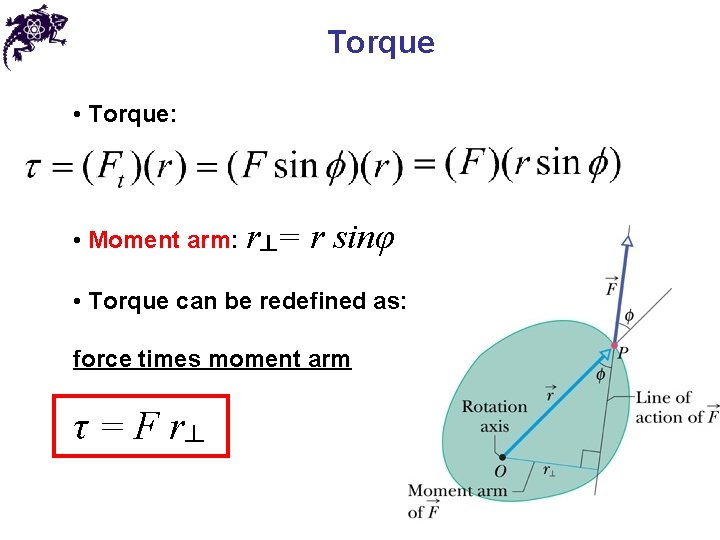
Torque • Torque: • Moment arm: r┴= r sinφ • Torque can be redefined as: force times moment arm τ = F r┴

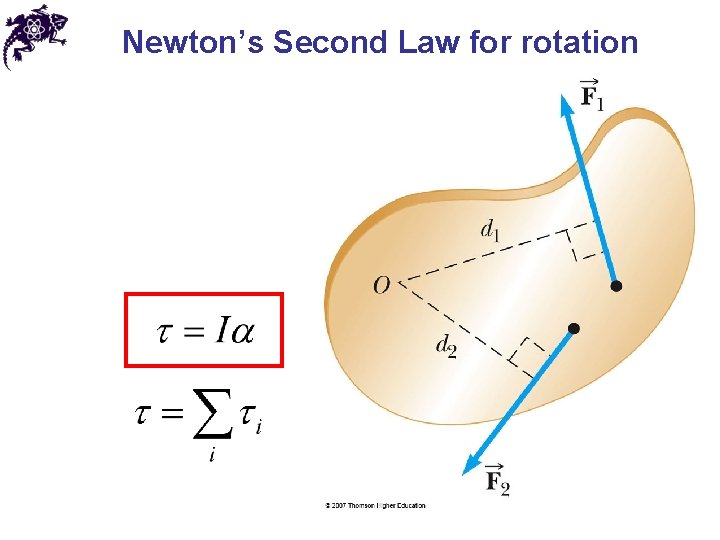
Newton’s Second Law for rotation • Consider a particle rotating under the influence of a force • For tangential components • Similar derivation for rigid body

Newton’s Second Law for rotation

Chapter 10 Problem 57 A 2. 4 -kg block rests on a slope and is attached by a string of negligible mass to a solid drum of mass 0. 85 kg and radius 5. 0 cm, as shown in the figure. When released, the block accelerates down the slope at 1. 6 m/s 2. Find the coefficient of friction between block and slope.

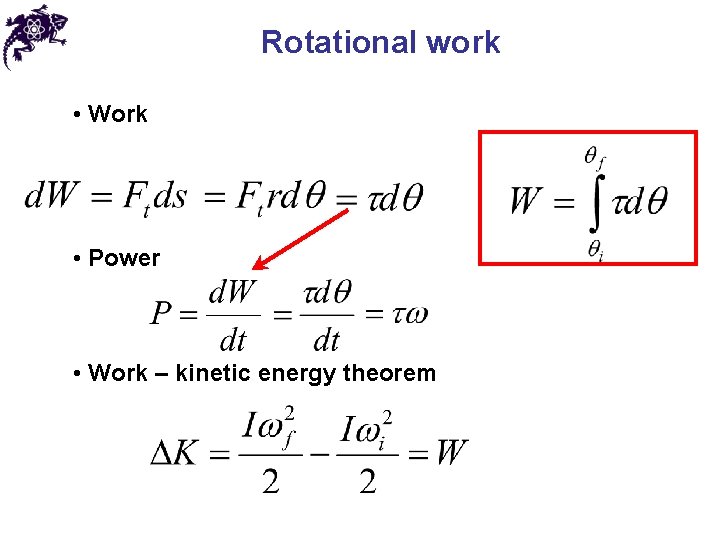
Rotational work • Work • Power • Work – kinetic energy theorem

Corresponding relations for translational and rotational motion

Smooth rolling • Smooth rolling – object is rolling without slipping or bouncing on the surface • Center of mass is moving at speed v. CM • Point of momentary contact between the two surfaces is moving at speed v. CM s = θR ds/dt = d(θR)/dt = R dθ/dt v. CM = ds/dt = ωR

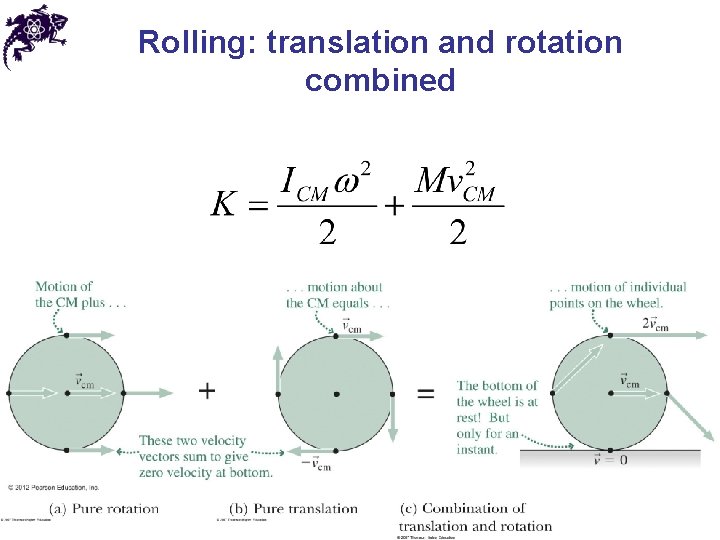
Rolling: translation and rotation combined • Rotation – all points on the wheel move with the same angular speed ω • Translation – all point on the wheel move with the same linear speed v. CM

Rolling: translation and rotation combined

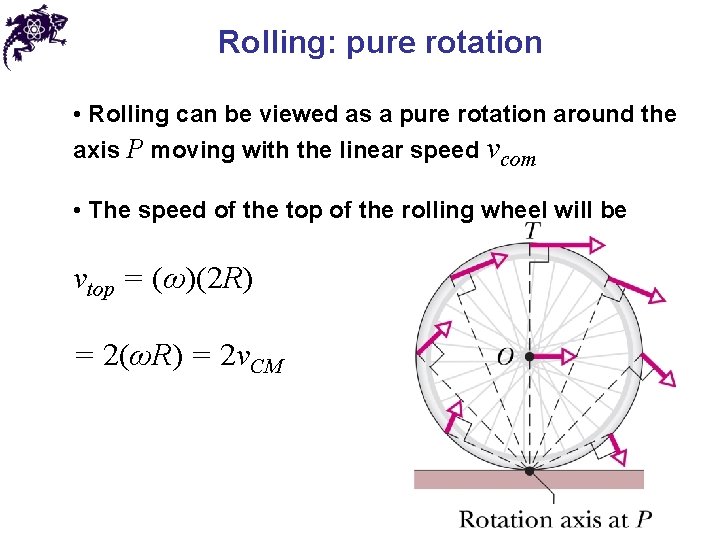
Rolling: pure rotation • Rolling can be viewed as a pure rotation around the axis P moving with the linear speed vcom • The speed of the top of the rolling wheel will be vtop = (ω)(2 R) = 2(ωR) = 2 v. CM

Friction and rolling • Smooth rolling is an idealized mathematical description of a complicated process • In a uniform smooth rolling, P is at rest, so there’s no tendency to slide and hence no friction force • In case of an accelerated smooth rolling a. CM = α R fs opposes tendency to slide

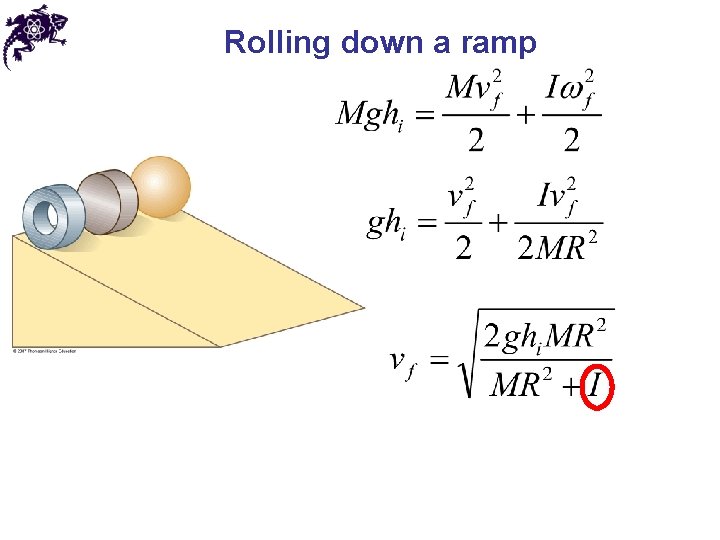
Rolling down a ramp

Chapter 10 Problem 39 What fraction of a solid disk’s kinetic energy is rotational if it’s rolling without slipping?

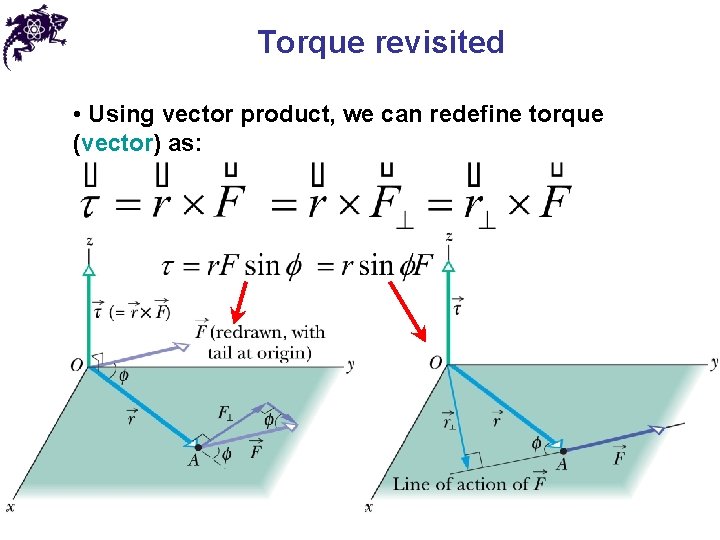
Vector product of two vectors • The result of the vector (cross) multiplication of two vectors is a vector • The magnitude of this vector is • Angle φ is the smaller of the two angles between and

Vector product of two vectors • Vector is perpendicular to the plane that contains vectors and its direction is determined by the right-hand rule • Because of the right-hand rule, the order of multiplication is important (commutative law does not apply) • For unit vectors

Vector product in unit vector notation

Torque revisited • Using vector product, we can redefine torque (vector) as:

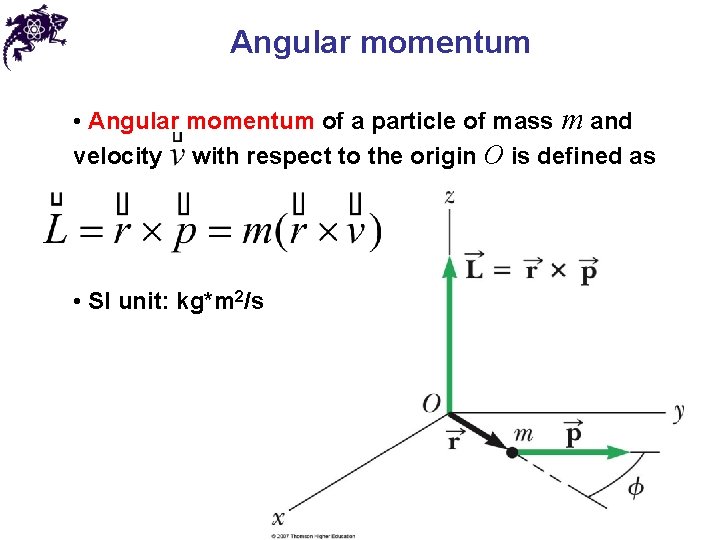
Angular momentum • Angular momentum of a particle of mass m and velocity with respect to the origin O is defined as • SI unit: kg*m 2/s

Newton’s Second Law in angular form

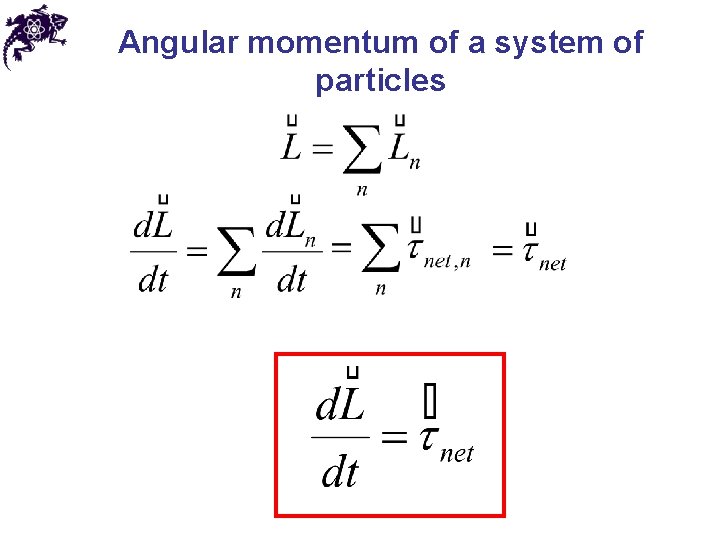
Angular momentum of a system of particles

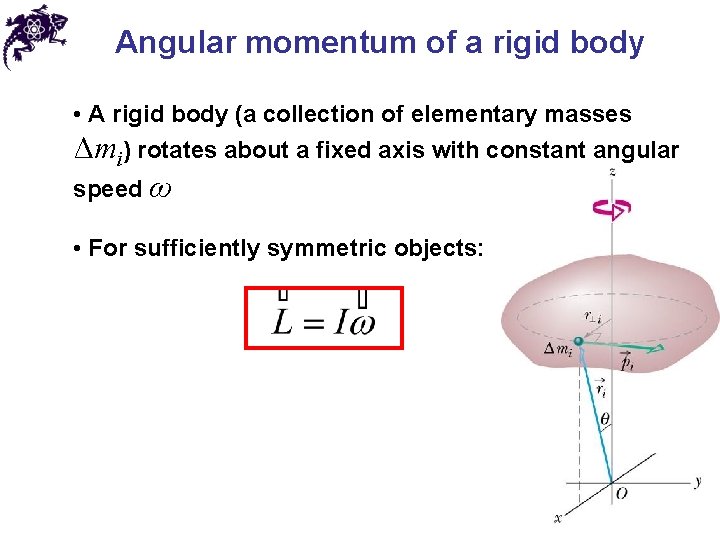
Angular momentum of a rigid body • A rigid body (a collection of elementary masses Δmi) rotates about a fixed axis with constant angular speed ω • For sufficiently symmetric objects:

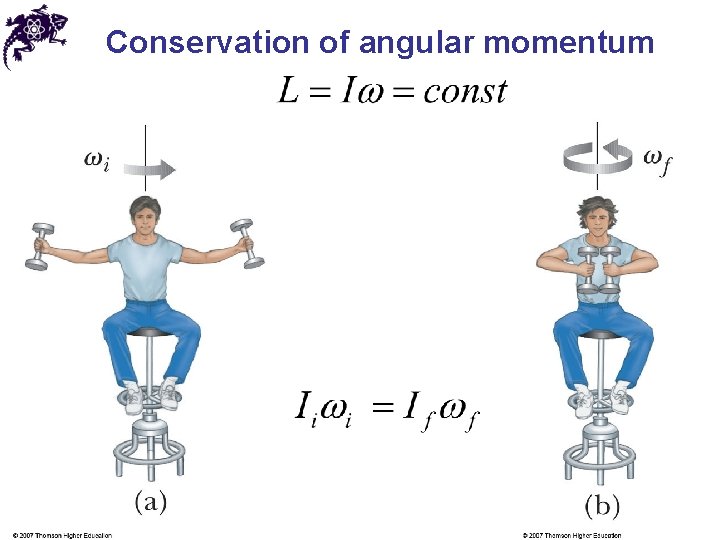
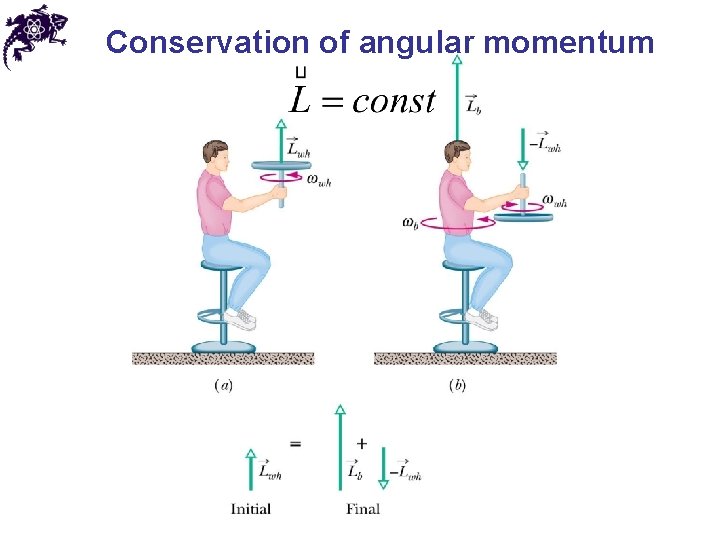
Conservation of angular momentum • From the Newton’s Second Law • If the net torque acting on a system is zero, then • If no net external torque acts on a system of particles, the total angular momentum of the system is conserved (constant) • This rule applies independently to all components

Conservation of angular momentum

Conservation of angular momentum

More corresponding relations for translational and rotational motion

Chapter 11 Problem 28 A skater has rotational inertia 4. 2 kg·m 2 with his fists held to his chest and 5. 7 kg·m 2 with his arms outstretched. The skater is spinning at 3. 0 rev/s while holding a 2. 5 -kg weight in each outstretched hand; the weights are 76 cm from his rotation axis. If he pulls his hands in to his chest, so they’re essentially on his rotation axis, how fast will he be spinning?

Questions?

Answers to the even-numbered problems Chapter 10 Problem 24 0. 072 N⋅m

Answers to the even-numbered problems Chapter 10 Problem 30 2. 58 × 1019 N⋅m

Answers to the even-numbered problems Chapter 10 Problem 40 hollow

Answers to the even-numbered problems Chapter 11 Problem 16 69 rad/s; 19° west of north

Answers to the even-numbered problems Chapter 11 Problem 18 (a) 8. 1 N⋅m kˆ (b) 15 N⋅m kˆ

Answers to the even-numbered problems Chapter 11 Problem 24 1. 7 × 10 -2 J⋅s

Answers to the even-numbered problems Chapter 11 Problem 26 (a) 1. 09 rad/s (b) 386 J

Answers to the even-numbered problems Chapter 11 Problem 30 along the x-axis or 120° clockwise from the x-axis

Answers to the even-numbered problems Chapter 11 Problem 42 26. 6°