Chapter9 Multiple Integrals In this Chapter n 1

Chapter-9 Multiple Integrals

In this Chapter: n 1 Double Integrals over Rectangles n 2 Double Integrals over General Regions n 3 Double Integrals in Polar Coordinates n 4 Applications of Double Integrals n 5 Triple Integrals n 6 Triple Integrals in Cylindrical Coordinates n 7 Triple Integrals in Spherical Coordinates n 8 Change of Variables in Multiple Integrals

What is a definite Integral?

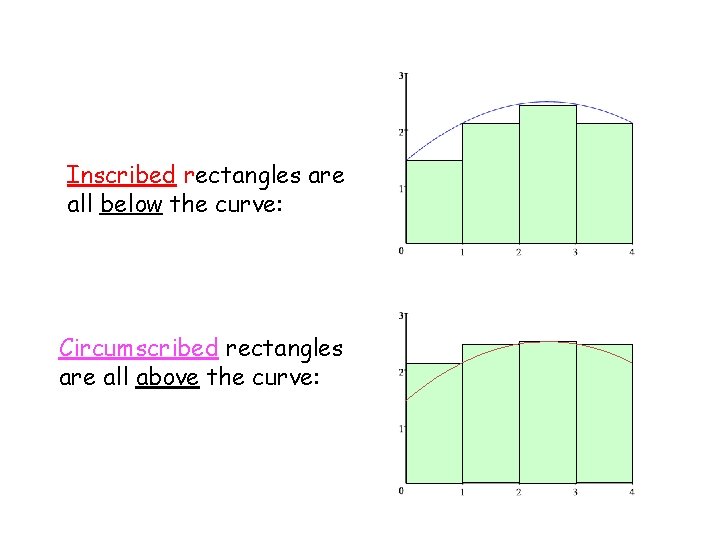
Inscribed rectangles are all below the curve: Circumscribed rectangles are all above the curve:

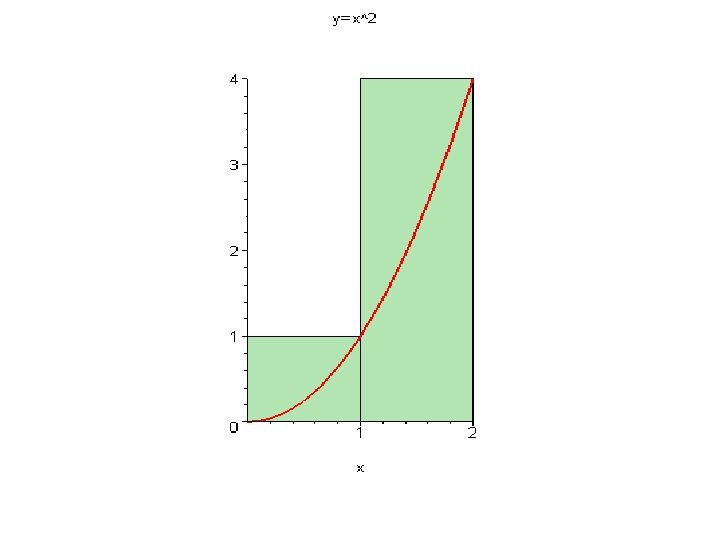
By taking the limit as n (the number of rectangles) approaches infinity, the actual area is approached.

Riemann Sum The area under the curve is subdivided into n subintervals. Each subinterval is treated as a rectangle. The area of all subintervals are added to determine the area under the curve. There are several variations of Riemann sum as applied to composite integration.

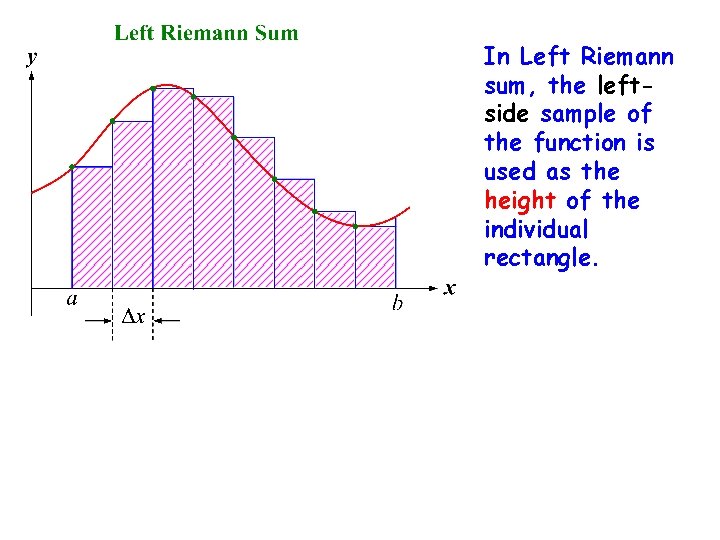
In Left Riemann sum, the leftside sample of the function is used as the height of the individual rectangle.

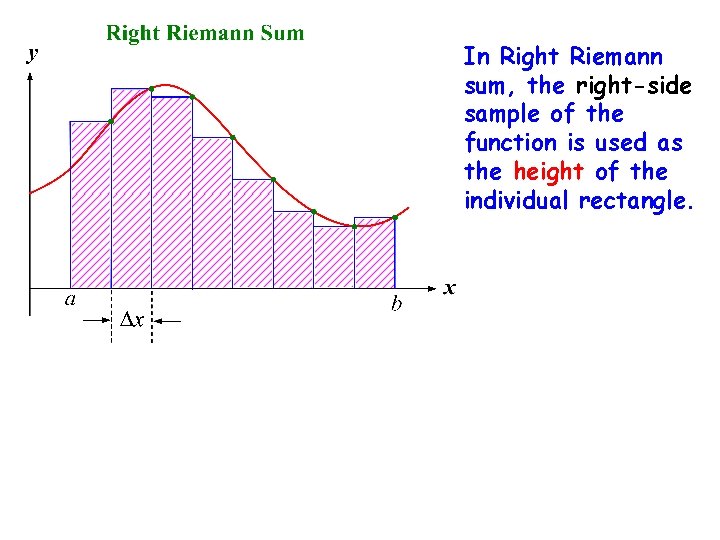
In Right Riemann sum, the right-side sample of the function is used as the height of the individual rectangle.

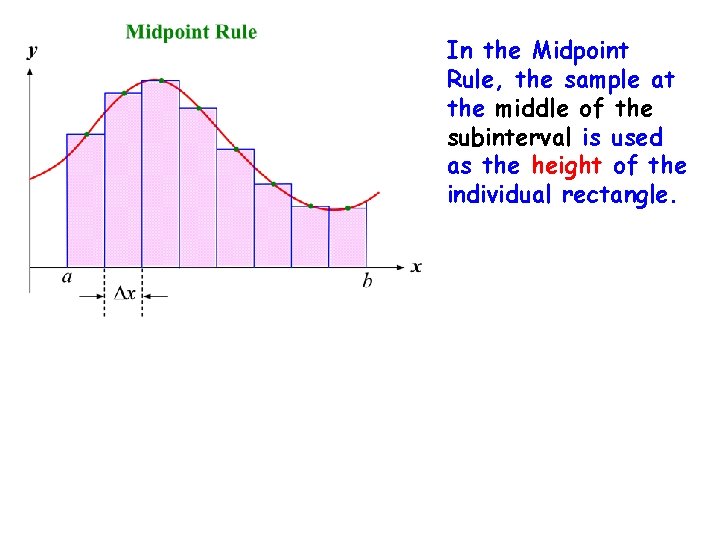
In the Midpoint Rule, the sample at the middle of the subinterval is used as the height of the individual rectangle.

Riemann Sum Definition: A sum such as the one below is called a Riemann sum.

Note that the very small change in becomes dx. x

Multiple integrals

Multiple Integrals • In this chapter, we extend the idea of a definite integral to double and triple integrals of functions of two or three variables. • These ideas are then used to compute volumes, masses, and centroids of more general regions , probabilities when two random variables are involved.

• We will see that polar coordinates are useful in computing double integrals over some types of regions. Triple Integrals: – Cylindrical coordinates – Spherical coordinates

Double Integrals • Just as our attempt to solve the area problem led to the definition of a definite integral, we now seek to find the volume of a solid. • In the process, we arrive at the definition of a double integral.

- With functions of one variable, we integrated over interval (one-dimensional space) - How about functions of two-variables?

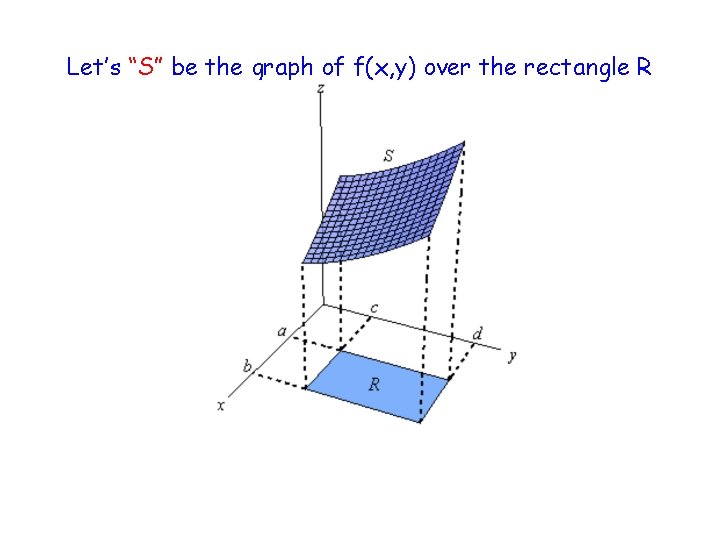
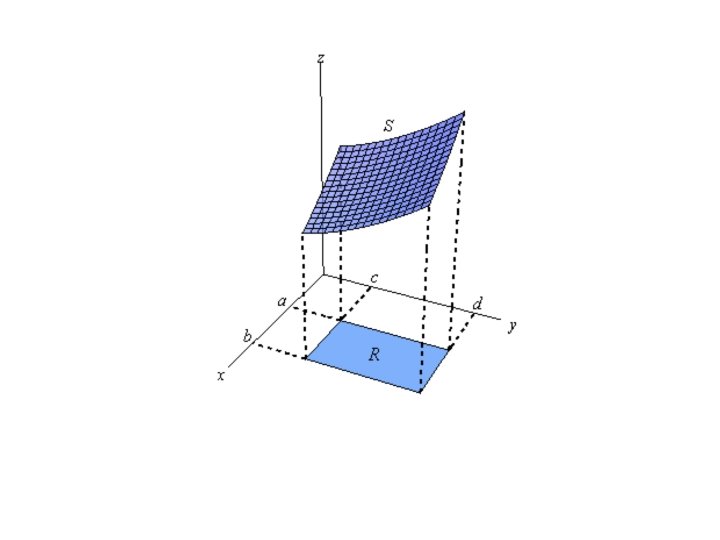
• Let’s consider a function f of two variables defined on a closed rectangle • R = [a, b] x [c, d] = {(x, y) in R 2 | a ≤ x ≤ b, c ≤ y ≤ d • and we first suppose that f(x, y) ≥ 0. – The graph of f is a surface with equation z = f(x, y).

Let’s “S” be the graph of f(x, y) over the rectangle R

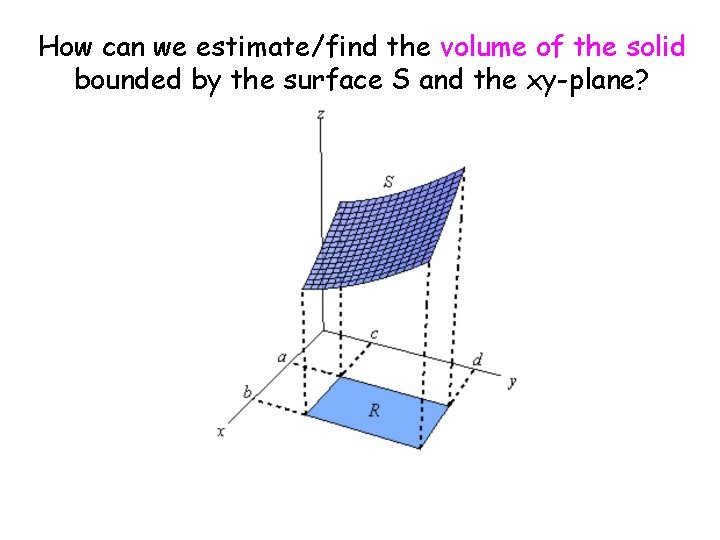
How can we estimate/find the volume of the solid bounded by the surface S and the xy-plane?

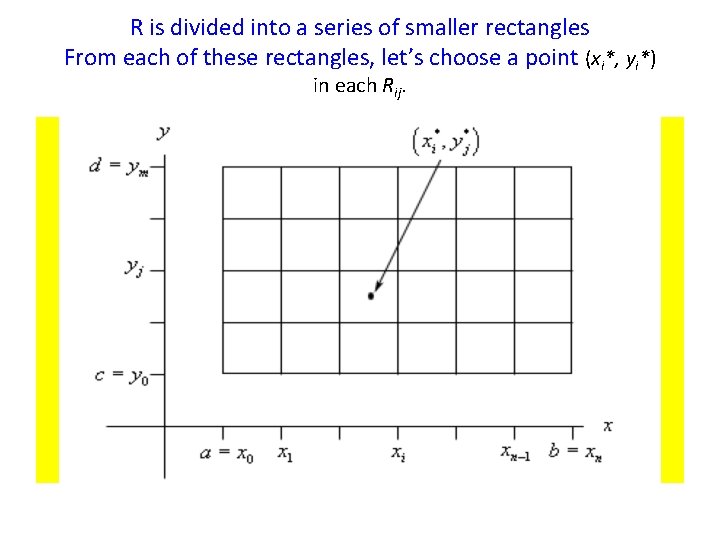
• The first step is to divide the rectangle R into subrectangles. – We divide the interval [a, b] into m subintervals [xi– 1, xi] of equal width ∆x = (b – a)/m. – Then, we divide [c, d] into n subintervals [yj– 1, yj] of equal width ∆y = (d – c)/n.

R is divided into a series of smaller rectangles From each of these rectangles, let’s choose a point (xi*, yi*) in each Rij.

Over each of these smaller rectangles, let’s construct a box whose height: f (xi*, yi*)

• What is the area of each rectangle? • ∆A = ∆x ∆y • How about its height? • f (xi*, yj*) So volume of the box ? f(xi *, yj *) ∆A

Volume of the solid- double sum?

• Our intuition tells us that the approximation given in becomes better as m and n become larger and larger. • So, we would expect that:

Double Integral • The double integral of f over the rectangle R is: if this limit exists .

One Interpretation of the Double Integral: If f (x, y) ≥ 0, then the volume V of the solid that lies above the rectangle R and below the surface z=f (x, y) is

How to calculate this double Reimann sum Or Double Integral?

Midpoint rule for Double Integrals where xi is the midpoint of [xi-1, xi] midpoint of [yj-1, yj ]. and yj is the

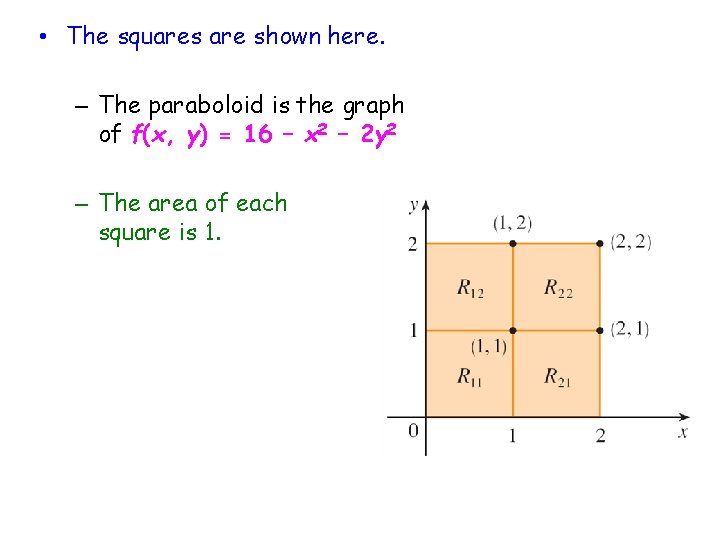
Example: Estimate the volume of the solid that lies above the square R = [0, 2] x [0, 2] and below the elliptic paraboloid z = 16 – x 2 – 2 y 2. – Divide R into four equal squares (m = n= ? ) and choose the sample point to be the upper right corner of each square Rij.

• The squares are shown here. – The paraboloid is the graph of f(x, y) = 16 – x 2 – 2 y 2 – The area of each square is 1.

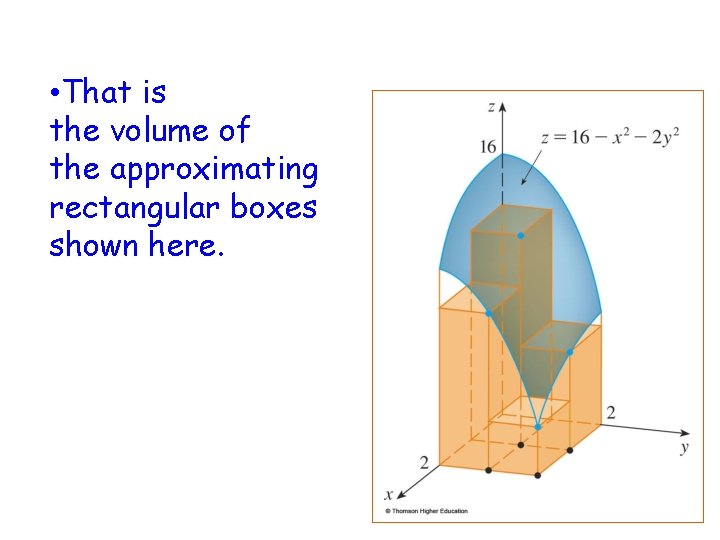
• Approximating the volume by the Riemann sum with m = n = 2, we have:

• That is the volume of the approximating rectangular boxes shown here.

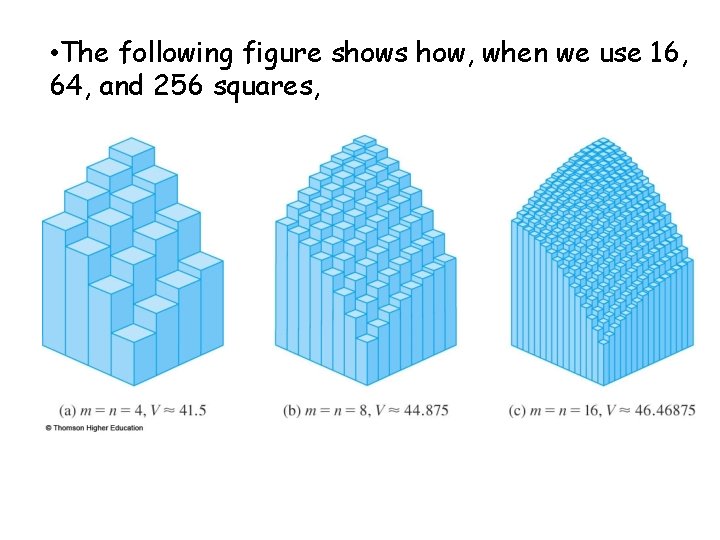
• The following figure shows how, when we use 16, 64, and 256 squares,

Class/Home work

Don’t be confused with Double sum!!!