Chapter V Illumination and Shaders 3 D Graphics

Chapter V Illumination and Shaders 3 D Graphics for Game Programming

What is Illumination? § Illumination or lighting refers to the techniques handling the interaction between light sources and objects. § The lighting models are divided into two categories. § § Local illumination considers only direct lighting in the sense that the illumination of a surface depends solely on the properties of the light sources and the surface materials. This has been dominant in real-time graphics. In the real world, however, every surface receives light indirectly. (Even though a light source is invisible from a particular point of the scene, light can still be transferred to the point through reflections or refractions from other surfaces of the scene. ) For indirect lighting, the global illumination (GI) model considers the scene objects as potential lighting sources. § Problems of interactive GI § § The cost is often too high to permit interactivity. The rasterization-based architecture of GPU is more suitable for local illumination. § Current status of GI § § Approximate GI instead of pursuing precise GI. Pre-compute GI, store the result in a texture, and use it at run time. 3 D Graphics for Game Programming 5 -2 2

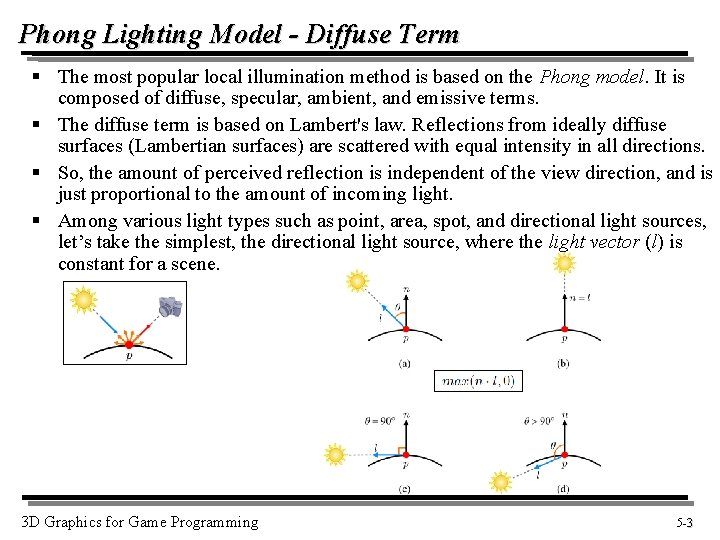
Phong Lighting Model - Diffuse Term § The most popular local illumination method is based on the Phong model. It is composed of diffuse, specular, ambient, and emissive terms. § The diffuse term is based on Lambert's law. Reflections from ideally diffuse surfaces (Lambertian surfaces) are scattered with equal intensity in all directions. § So, the amount of perceived reflection is independent of the view direction, and is just proportional to the amount of incoming light. § Among various light types such as point, area, spot, and directional light sources, let’s take the simplest, the directional light source, where the light vector (l) is constant for a scene. 3 D Graphics for Game Programming 5 -3 3

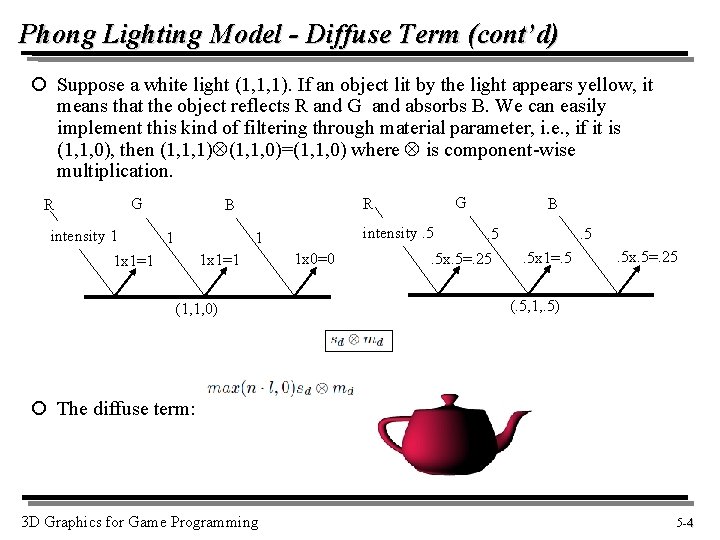
Phong Lighting Model - Diffuse Term (cont’d) ¡ Suppose a white light (1, 1, 1). If an object lit by the light appears yellow, it means that the object reflects R and G and absorbs B. We can easily implement this kind of filtering through material parameter, i. e. , if it is (1, 1, 0), then (1, 1, 1) (1, 1, 0)=(1, 1, 0) where is component-wise multiplication. G R intensity 1 1 intensity. 5 1 1 x 1=1 G R B (1, 1, 0) 1 x 0=0 B. 5 . 5 x. 5=. 25 . 5. 5 x 1=. 5 . 5 x. 5=. 25 (. 5, 1, . 5) ¡ The diffuse term: 3 D Graphics for Game Programming 5 -4 4

Phong Lighting Model - Specular Term § The specular term is used to make a surface look shiny via highlights, and it requires view vector (v) and reflection vector (r) in addition to light vector (l). § Computing the reflection vector 3 D Graphics for Game Programming 5 -5 5

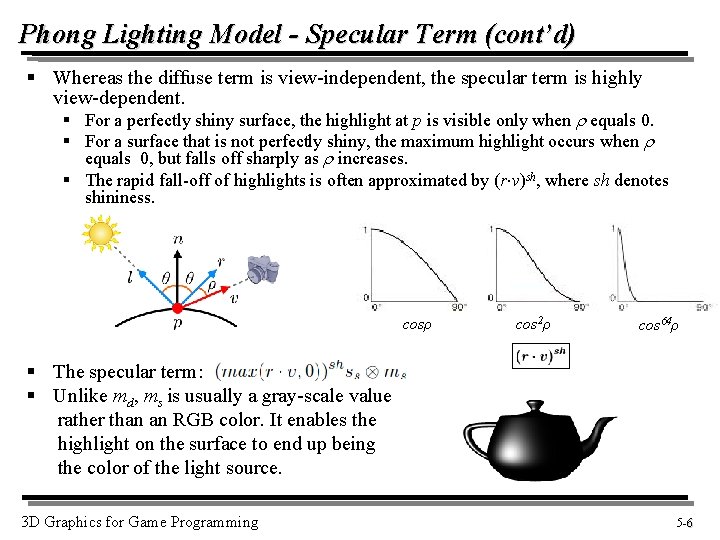
Phong Lighting Model - Specular Term (cont’d) § Whereas the diffuse term is view-independent, the specular term is highly view-dependent. § For a perfectly shiny surface, the highlight at p is visible only when equals 0. § For a surface that is not perfectly shiny, the maximum highlight occurs when equals 0, but falls off sharply as increases. § The rapid fall-off of highlights is often approximated by (r v)sh, where sh denotes shininess. cosρ cos 2ρ cos 64ρ § The specular term: § Unlike md, ms is usually a gray-scale value rather than an RGB color. It enables the highlight on the surface to end up being the color of the light source. 3 D Graphics for Game Programming 5 -6 6

Phong Lighting Model - Specular Term (cont’d) 3 D Graphics for Game Programming 5 -7 7

Phong Lighting Model – Ambient and Emissive Terms § The ambient light describes the light reflected from the various objects in the scene, i. e. , it accounts for indirect lighting. § As the ambient light has bounced around so much in the scene, it arrives at a surface point from all directions, and reflections from the surface point are also scattered with equal intensity in all directions. § The last term of the Phong model is the emissive term me that describes the amount of light emitted by a surface itself. 3 D Graphics for Game Programming 5 -8 8

Phong Lighting Model § The Phong model sums the four terms!! 3 D Graphics for Game Programming 5 -9 9

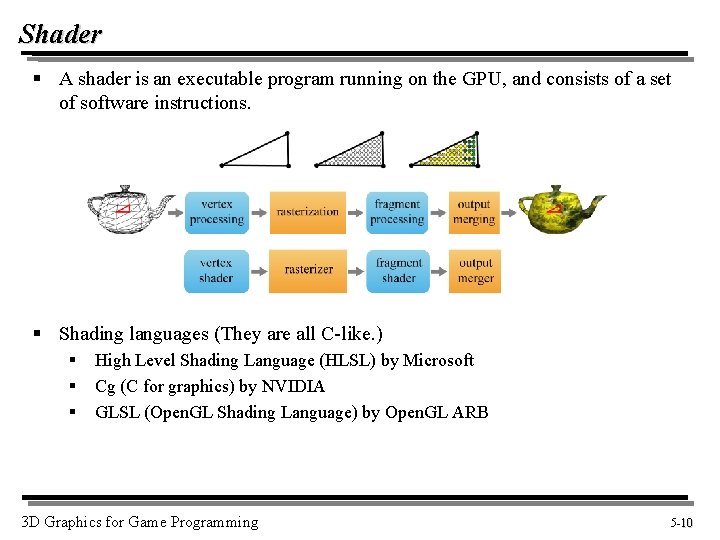
Shader § A shader is an executable program running on the GPU, and consists of a set of software instructions. § Shading languages (They are all C-like. ) § § § High Level Shading Language (HLSL) by Microsoft Cg (C for graphics) by NVIDIA GLSL (Open. GL Shading Language) by Open. GL ARB 3 D Graphics for Game Programming 5 -10 10

Shader (cont’d) § Special data types such as float 4 (a four-element vector) and float 2 x 3 (a 2 x 3 element matrix) are supported. § Two kinds of input data § Varying data: unique to each execution of a shader (e. g. , vertex position) § Uniform data: constant for multiple executions of a shader (e. g. , world matrix) – specified as global variables or with the keyword uniform § Intrinsic functions such as mul() 3 D Graphics for Game Programming 5 -11 11

Shader (cont’d) § All varying inputs must have associated semantic labels such as POSITION and TEXCOORD 0. The semantics can be assigned by two methods: § § Appending a colon and the semantic label to the parameter declaration. Defining a structure with semantics assigned to the structure members. § The output data can be described using the keyword out if the data are included in the parameter list. (Otherwise, the return value of a shader is automatically taken as the output. ) § All outputs must have associated semantic labels. A shader provides output data to the next stage of the rendering pipeline, and the output semantics are used to specify how the data should be linked to the inputs of the next stage. For example, the output semantic POSITION represents the clip-space position of the transformed vertex that is fed to the rasterizer. 3 D Graphics for Game Programming 5 -12 12

Per-vertex Lighting § The vertex shader processes a vertex at a time. 3 D Graphics for Game Programming 5 -13 13

Per-vertex Lighting (cont’d) § Recall what the rasterizer does. § The simplest fragment shader for per-vertex lighting 3 D Graphics for Game Programming 5 -14 14

Problems in Per-vertex Lighting § Per-vertex lighting followed by “color interpolation” makes the colors at vertices evenly interpolated along the edges and then along the scan lines. So, highlights inside a triangle cannot be caught. § Such a problem of per-vertex lighting can be overcome by employing perfragment lighting, which is often called a normal interpolation shading. 3 D Graphics for Game Programming 5 -15 15

Problems in Per-vertex Lighting (cont’d) § When the camera moves, the scene rendered by per-vertex lighting can have a popping effect. 3 D Graphics for Game Programming 5 -16 16

Per-fragment Lighting § The vertex shader computes the clip-space vertex position (It’s required!) and outputs the world-space position and normal of each vertex to the rasterizer. § The fragment shader processes a fragment at a time. 3 D Graphics for Game Programming 5 -17 17

Ivan Sutherland § Kendall Station at Boston (MIT) 3 D Graphics for Game Programming 4 -18 18

Ivan Sutherland (cont’d) Turing Award Steven A. Coons Award 1966 A. J. Perlis 1983 Ivan Sutherland 1969 Marvin Minsky 1985 Pierre Bezier 1971 John Mc. Carthy 1987 Donald Greenberg 1972 E. W. Dijkstra 1989 David Evans 1975 Herbert A. Simon 1991 Andries van Dam 1977 John Backus 1993 Ed Catmull 1980 C. Antony R. Hoare 1995 Jose Luis Encarnacao 1983 Ken Thompson 1997 James Foley Dennis M. Ritchie 1999 James Blinn 1984 Niklaus Wirth 2001 Lance Williams 1988 Ivan Sutherland … 1999 F. Brooks 2002 R. Rivest, A. Shamir, L. Adleman … 3 D Graphics for Game Programming 4 -19 19

Ivan Sutherland (cont’d) § Ivan Sutherland's students § § § § Edwin Catmull - founder of Pixar and now president of Walt Disney and Pixar Animation Studios James H. Clark - founder of Silicon Graphics and Netscape John Warnock - founder of Adobe Nolan Bushnell - founder of Atari Alan Kay - inventor of the Smalltalk language Henri Gouraud - inventor of Gouraud shading algorithm (per-vertex lighting with Phong model) Bui Tuong Phong - inventor of Phong shading algorithm (per-fragment lighting with Phong model) 3 D Graphics for Game Programming 4 -20 20

Global Illumination – Ray Tracing § When a primary ray is shot and intersects an object, three secondary rays would be spawned: a shadow ray, a reflection ray, and a refraction ray. 3 D Graphics for Game Programming 5 -21 21

Global Illumination – Ray Tracing § The refraction ray is computed using the Snell’s law. 3 D Graphics for Game Programming 5 -22 22

Global Illumination – Ray Tracing (cont’d) 3 D Graphics for Game Programming 5 -23 23

Global Illumination – Radiosity § Radiosity algorithm simulates bounced light between diffuse surfaces. Light hitting a surface is reflected back to the environment. As light bounces around an environment, each surface of the environment works itself as a light source. The radiosity algorithm does not distinguish light sources from the objects to be lit by the light sources. § Radiosity of a surface describes the brightness of the surface, and is defined to be the rate at which light leaves the surface. § All surfaces of the scene are subdivided into patches, and then the form factors among all the patches are computed. The form factor describes the fraction of light that leaves one patch and arrives at another. 3 D Graphics for Game Programming 5 -24 24

Global Illumination – Radiosity (cont’d) § In principle, the point-to-point form factor needs to be integrated to define a patch-to-patch form factor. Assuming the radiosities are constant over the extent of a patch, computing the patch-to -patch form factor is reduced to computing a point-to-patch form factor. § The form factor between p and sj is conceptually calculated using the hemisphere placed at p. The form factor is defined to be the area projected on the hemisphere's base divided by the base area. § The hemisphere is often replaced by the hemicube. The per-pixel form factors can be pre-computed. Then, patch sj is projected onto the hemicube. The form factor is the sum of the form factors of the pixels covered by the projection. 3 D Graphics for Game Programming 5 -25 25

Global Illumination – Radiosity (cont’d) § Once the form factors are computed, solve the linear system. § The radiosity of each patch is obtained. Then, the irradiance of each patch can also be computed as Bi-Ei. 3 D Graphics for Game Programming 5 -26 26

Global Illumination – Radiosity (cont’d) 3 D Graphics for Game Programming 5 -27 27