Chapter two Regular expressions and Finite automata Regular

Chapter two Regular expressions and Finite automata

Regular expressions A finitary denotation of certain kinds of infinitary languages over Σ. Bases: ∅ denotes L∅ = ∅ σ denotes Lσ = {σ} for any σ ∈ Σ Induction: r + s denotes Lr ∪ Ls r · s denotes Lr · Ls; r* denotes Lr* Notation: r is a regular expression which denotes a set of strings Examples: 6/8/2021 a(a + b)* All binary strings which contain 11. All binary strings which exclude 11. Theory of Computation: Chapter 2 2

Example Claim: (0 + 10)*(1 + 10)* is the language of strings in which every pair of adjacent zeros appears before any pair of adjacent ones. Justification: w ∈ (0 + 10)*(1 + 10)* implies w = w₁w₂ with w₁ ∈ (0 + 10)* and w₂ ∈ (1 + 10)*. Since (0 + 10)* cannot have double ones and (1 + 10)* cannot have double zeros we cannot have a 11 before a 00. So every double zero appears before any double one. 6/8/2021 Theory of Computation: Chapter 2 3

Continued Conversely any string w ≠ … 11… 00…, i. e. w = … 00… 11… with this property can be written w = xyz where x is the shortest prefix containing all the double zeros (i. e. ε or ending in 0 or 00) and z is the shortest suffix containing all the double ones (i. e. ε or beginning with 1 or 11). This is possible precisely because w satisfies the requirement of all double zeros before any double ones. Now see that y must be of the form (10)*. Since x ∈ (0 + 10)* and z ∈ (1 + 10)*, w = xyz ∈ (0 + 10)*(1 + 10)*, since (10)* is subsumed by its neighbors. 6/8/2021 Theory of Computation: Chapter 2 4

Identities ∅ is the additive identity: ∅·r = ∅ = r·∅ ∅+r=r=r+∅ ∅* is the multiplicative identity: ∅*·r = r·∅* = r where ∅* = {ε} r+r=r r*r* = r* (r*)* = r* r(st) = (rs)t r + s = s + r (r + s) + t = r + (s + t) r(s + t) = rs + rt (r + s)t = rt + st (r*s*)* = (r + s)* [HW problem] Hint: Regular operations are monotone: r ⊆ s ⇒ f(r) ⊆ f(s), where f is ‘*’, or ‘+ t’, or ‘· t’, or ‘t ·’. 6/8/2021 Theory of Computation: Chapter 2 5

Disjunctive normal form (DNF) Theorem: Every regular expression can be written as r₁ +…+ rᵢ where each individual term does not containing the ‘+’ symbol. Proof: By structural induction. The bases are trivial, as well as r + s. r · s = (r₁ + … + rᵢ)·(s₁ + … + sⱼ) by induction hypothesis. Use the distributive laws to finish. r* = (r₁ + … + rᵢ)* by induction hypothesis. Use the identity (r + s)* = (r*s*)* to show that (r₁ + … + rᵢ)* = (r₁* ····· rᵢ*)* follows by induction. 6/8/2021 Theory of Computation: Chapter 2 6

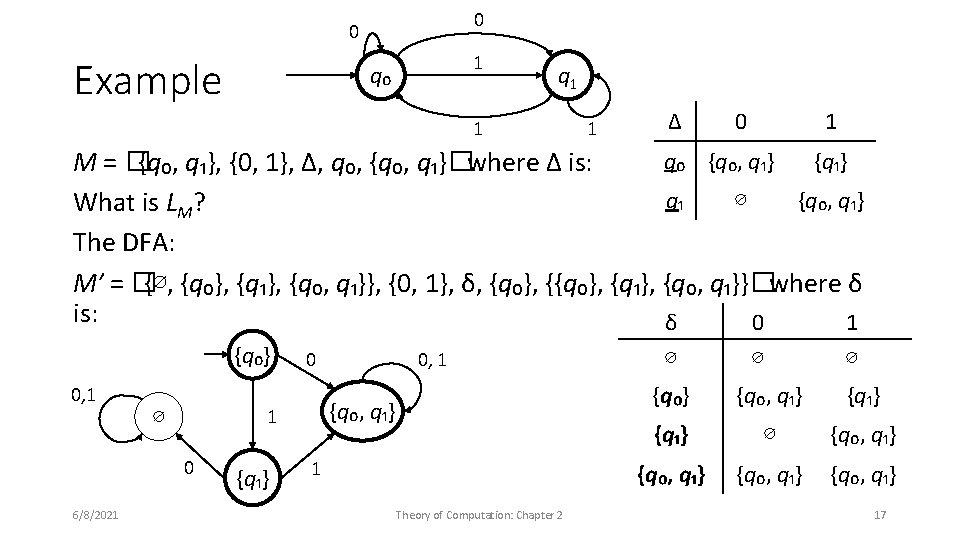
Deterministic finite automaton The input tape contains symbols from Σ. A read head moves left-toright across the input, and the state of the machine is in a finite control. Formally: �Q, Σ, δ, s, F�where Q is a finite set of states Σ is the (finite) alphabet δ : Q × Σ → Q is the transition function s ∈ Q is the start state F ⊆ Q is the set of final states 6/8/2021 Theory of Computation: Chapter 2 7

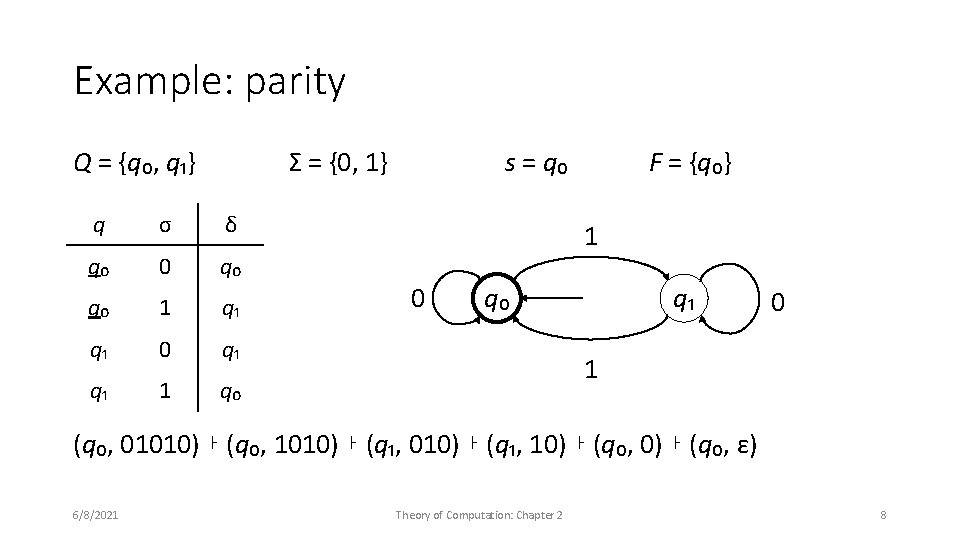
Example: parity Q = {q₀, q₁} Σ = {0, 1} q σ δ q₀ 0 q₀ q₀ 1 q₁ q₁ 0 q₁ q₁ 1 q₀ s = q₀ F = {q₀} 1 0 q₀ q₁ 0 1 (q₀, 01010) ⊦ (q₀, 1010) ⊦ (q₁, 10) ⊦ (q₀, ε) 6/8/2021 Theory of Computation: Chapter 2 8

Algorithm (operational semantics) q←s h← 1 while σ(h) ≠ blank q ← δ(q, σ(h)) h←h+1 If q ∈ F then accept Else reject 6/8/2021 {M begins in state s} {with head leftmost} {as long as head is reading a symbol} {change state} {move head right one symbol} {accept if we end in a final state} {reject otherwise} Theory of Computation: Chapter 2 9

Formal (denotational) semantics A configuration (q, w) of M is an element of Q × Σ*, where w is the portion of the input that hasn’t been read yet. A configuration is terminal if w = ε. The yields function ⊦ : Q × Σ⁺ → Q × Σ* is a map (q, σw) ⊦ (δ(q, σ), w) M accepts w if and only if (s, w) ⊦* (f, ε) for some f ∈ F. 6/8/2021 Theory of Computation: Chapter 2 10

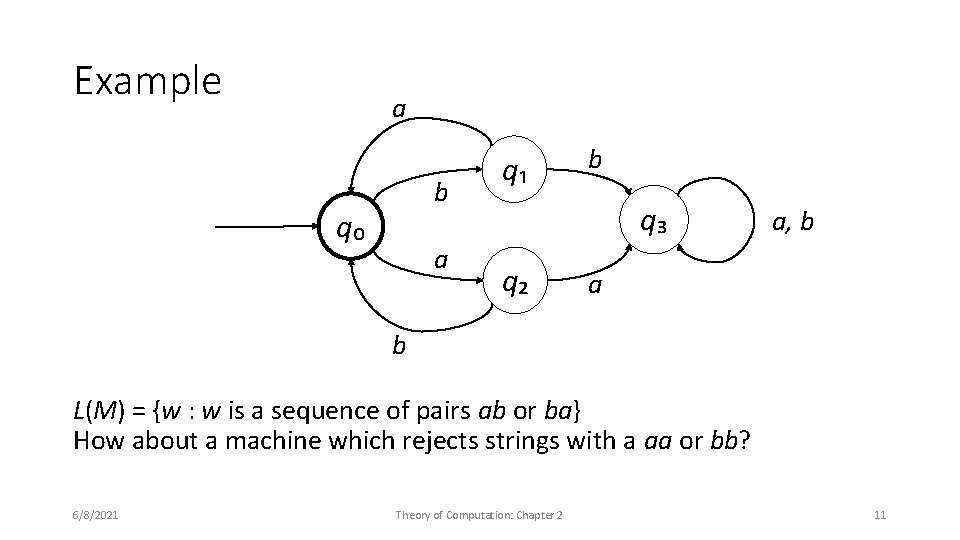
Example a b q₀ a q₁ b q₃ q₂ a, b a b L(M) = {w : w is a sequence of pairs ab or ba} How about a machine which rejects strings with a aa or bb? 6/8/2021 Theory of Computation: Chapter 2 11

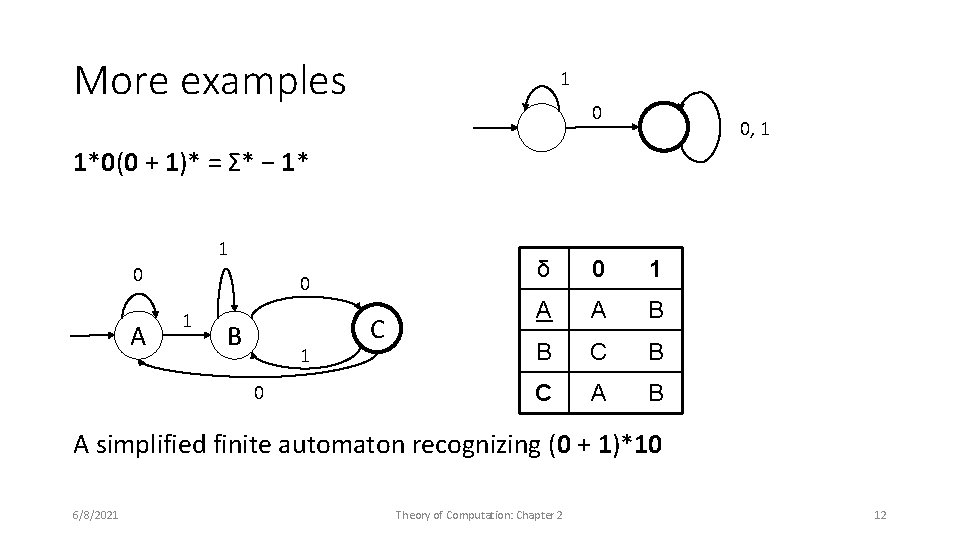
More examples 1 0 0, 1 1*0(0 + 1)* = Σ* − 1* 1 0 A 0 1 B 1 0 C δ 0 1 A A B B C A B A simplified finite automaton recognizing (0 + 1)*10 6/8/2021 Theory of Computation: Chapter 2 12

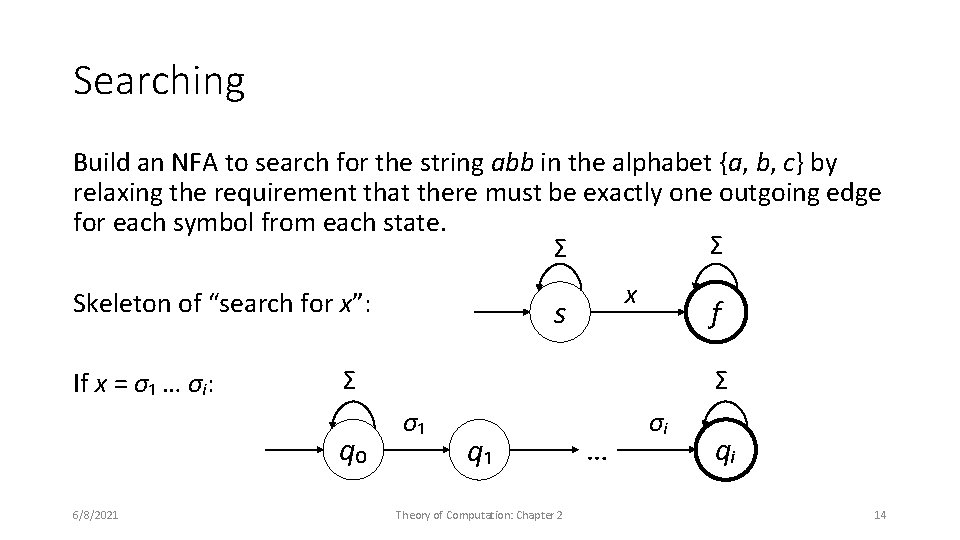
Searching Build an NFA to search for the string abb in the alphabet {a, b, c} by relaxing the requirement that there must be exactly one outgoing edge for each symbol from each state. Σ Σ Skeleton of “search for x”: If x = σ₁ … σᵢ: s f Σ q₀ 6/8/2021 x Σ σ₁ q₁ Theory of Computation: Chapter 2 … σᵢ qᵢ 14

Nondeterministic finite automaton Same as deterministic except that the transition function is a relation. Δ⊆Q×Σ×Q i. e. Δ : Q × Σ → 2 Q p σ q iff q ∈ Δ(p, σ) The yields relation is no longer a function: (q, σx) ⊦ (q′, x) ⇔ q′ ∈ Δ(q, σ) Acceptance is the same: M accepts w iff (s, w) ⊦* (f, ε) for some f ∈ F 6/8/2021 Theory of Computation: Chapter 2 15

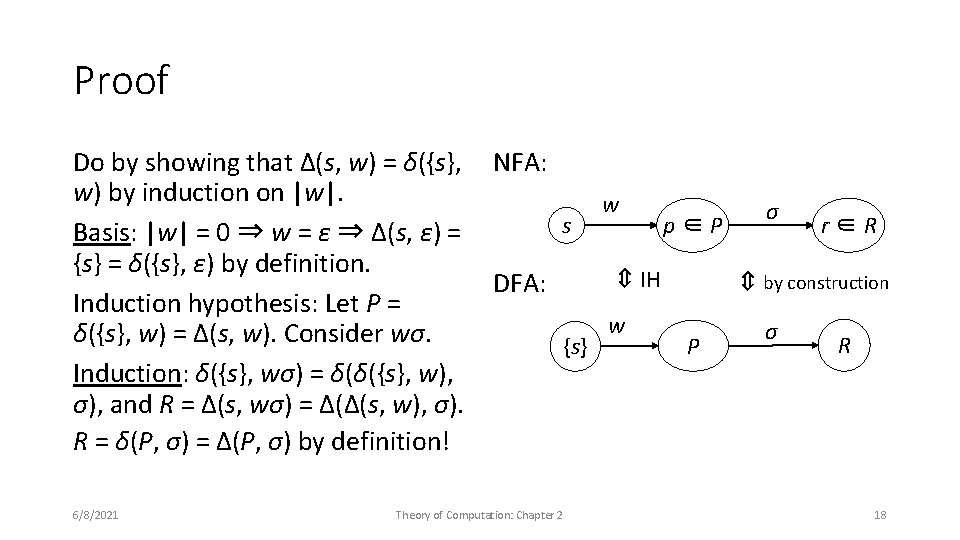
NFA to DFA conversion Define: δ(p, ε) = p; δ(P, σ) = {δ(p, σ) : p ∈ P} ; δ(P, wσ) = δ(δ(P, w), σ) Δ(P, σ) = ⋃ {Δ(p, σ) : p ∈ P} ; Δ(p, ε) ≡ {p}; Δ(P, wσ) = Δ(Δ(P, w), σ) Theorem: For every NFA M = �Q, Σ, Δ, s, F�, there is an equivalent DFA. Proof: Let M′ = � 2 Q, Σ, δ(P ⊆ Q, σ) = Δ(P, σ) , {s}, {P ⊆ Q : P ∩ F ≠ ∅}� Idea: A single state in M′ is a set of states in M. Show M can reach f ∈ F iff M′ reaches a state containing f. 6/8/2021 Theory of Computation: Chapter 2 16

Proof s DFA: w {s} Theory of Computation: Chapter 2 w σ p∈P IH ⇔ 6/8/2021 NFA: ⇔ Do by showing that Δ(s, w) = δ({s}, w) by induction on |w|. Basis: |w| = 0 ⇒ w = ε ⇒ Δ(s, ε) = {s} = δ({s}, ε) by definition. Induction hypothesis: Let P = δ({s}, w) = Δ(s, w). Consider wσ. Induction: δ({s}, wσ) = δ(δ({s}, w), σ), and R = Δ(s, wσ) = Δ(Δ(s, w), σ). R = δ(P, σ) = Δ(P, σ) by definition! P r∈R by construction σ R 18

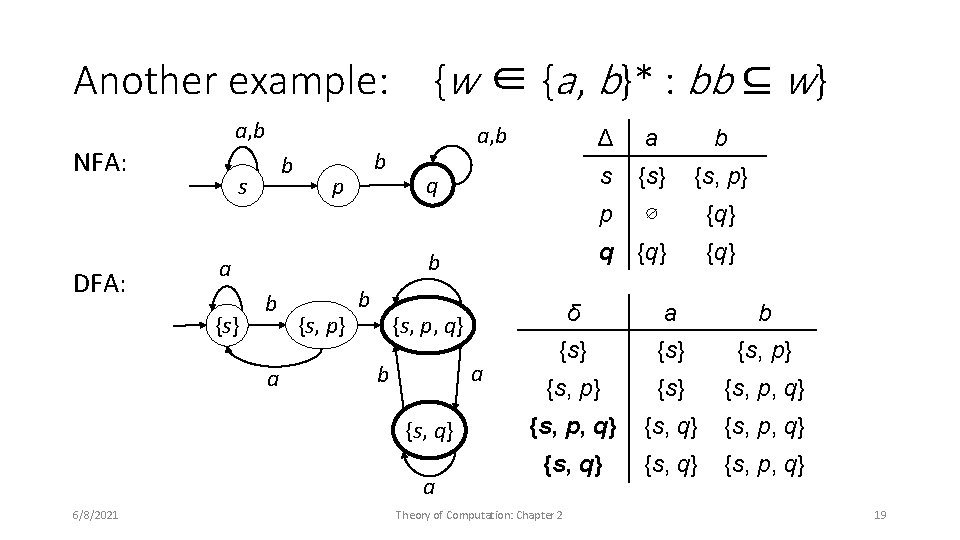
Another example: {w ∈ {a , b}* : bb ⊆ w} a, b NFA: DFA: b s b p q b a {s} a, b b a {s, p} b {s, p, q} a b {s, q} a 6/8/2021 Δ a b s {s} {s, p} p ∅ {q} q {q} δ a b {s} {s, p} {s} {s, p, q} {s, q} {s, p, q} Theory of Computation: Chapter 2 19

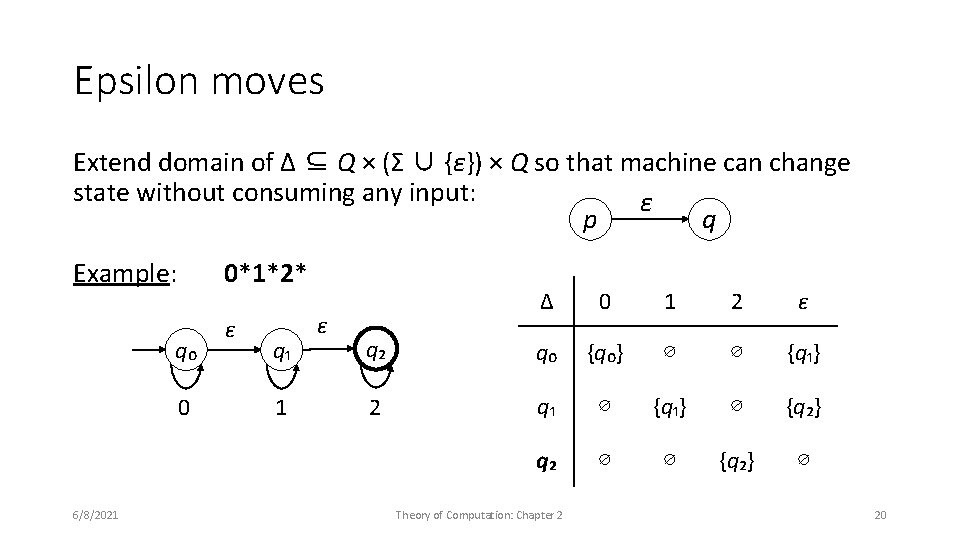
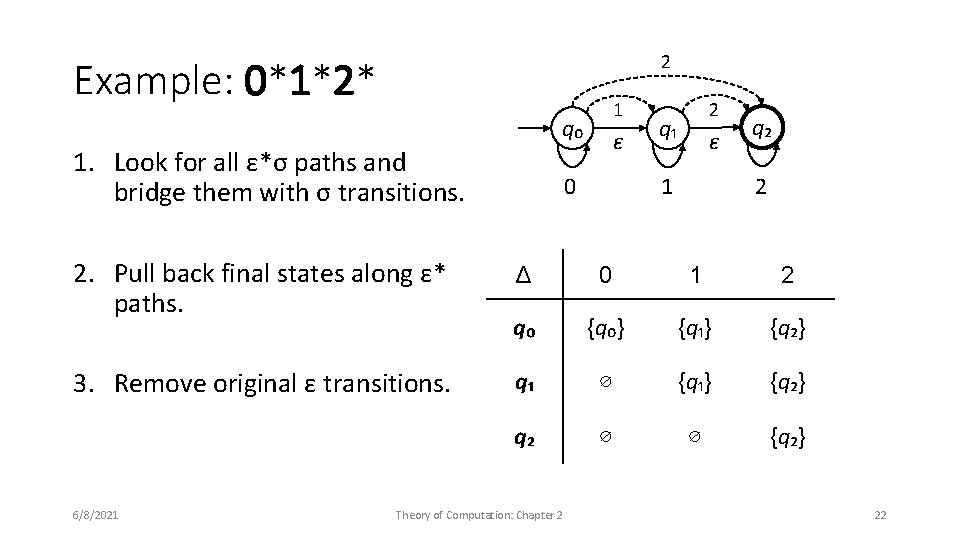
Epsilon moves Extend domain of Δ ⊆ Q × (Σ ∪ {ε}) × Q so that machine can change state without consuming any input: ε p q Example: 0*1*2* q₀ 0 6/8/2021 ε q₁ 1 ε Δ 0 1 2 ε q₂ q₀ {q₀} ∅ ∅ {q₁} 2 q₁ ∅ {q₁} ∅ {q₂} q₂ ∅ ∅ {q₂} ∅ Theory of Computation: Chapter 2 20

Eliminating ε-moves Let Δε* = Δ* ∩ [Q × {ε} × Q] be the transitive reflexive closure of the ε-edges. ε* So Δε*(p) = {q : (p, q) ∈ Δε*} p Extend Δ to Δ′(p, σ) = Δ(Δε*(p), σ) p Extend F to F′ = {p : Δε*(p) ∩ F ≠ ∅} q ε⁺ σ q σ p ε⁺ f Remove all ε-edges and claim that new machine is equivalent to the old. Idea: Break up ε-paths in old machine into ε*σ₁ … ε*σᵢε*. 6/8/2021 Theory of Computation: Chapter 2 21

2 Example: 0*1*2* 1 q₀ 1. Look for all ε*σ paths and bridge them with σ transitions. 2. Pull back final states along ε* paths. 3. Remove original ε transitions. 6/8/2021 ε 0 2 q₁ ε 1 q₂ 2 Δ 0 1 2 q₀ {q₀} {q₁} {q₂} q₁ ∅ {q₁} {q₂} q₂ ∅ ∅ {q₂} Theory of Computation: Chapter 2 22

Regular expression to NFA Theorem: Every regular language is accepted by some finite automata. Proof: By induction on the structure of a regular expression r. Bases: r=∅ r=σ Inductions: r₁ + r₂ r₁ · r₂ r* 6/8/2021 a machine that accepts nothing a machine that accepts only σ ∈ Σ nondeterministic parallelism nondeterministic serialism nondeterministic iteration Theory of Computation: Chapter 2 23

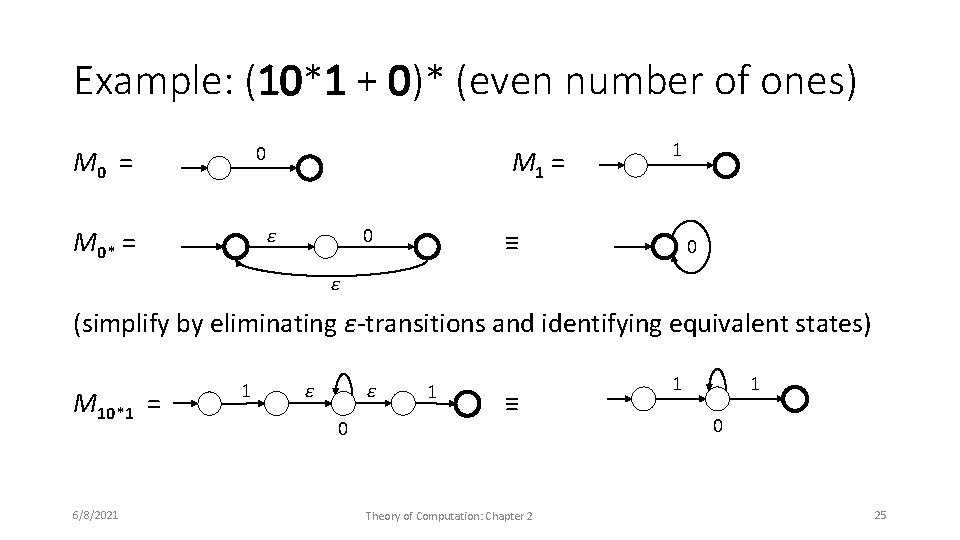
Example: (10*1 + 0)* (even number of ones) 0 M 0 = M 1 = ε M 0* = 0 1 ≡ 0 ε (simplify by eliminating ε-transitions and identifying equivalent states) M 10*1 = 6/8/2021 1 ε ε 0 1 ≡ Theory of Computation: Chapter 2 1 1 0 25

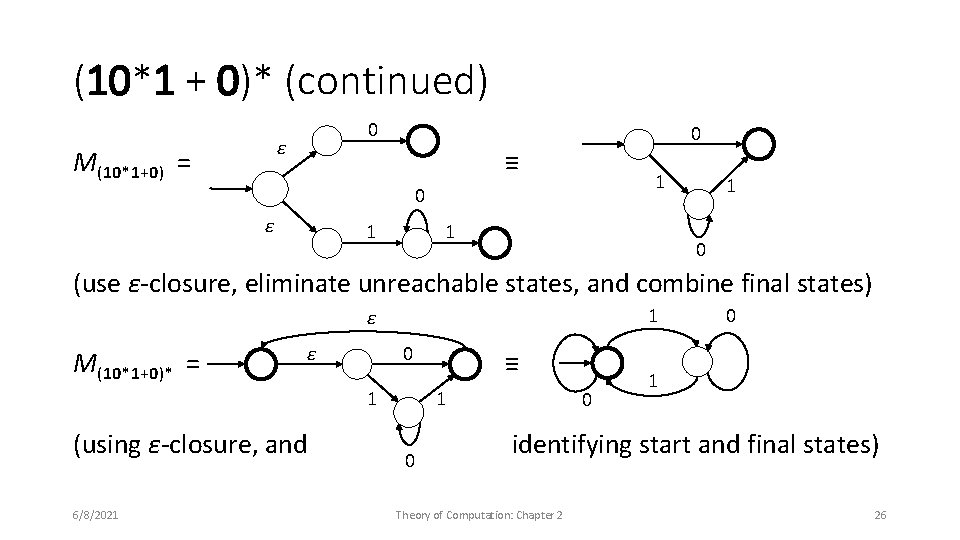
(10*1 + 0)* (continued) 0 ε M(10*1+0) = 0 ≡ 1 0 ε 1 1 1 0 (use ε-closure, eliminate unreachable states, and combine final states) 1 ε M(10*1+0)* = ε 0 1 (using ε-closure, and 6/8/2021 ≡ 1 0 0 0 1 identifying start and final states) Theory of Computation: Chapter 2 26

Finite automata to Regular expression Start: Number the states s = q 0, …, qn. Idea: Find a solution to: Aᵢ = {w ∈ Σ* : Δ(qᵢ, w) ∩ F ≠ ∅} when i = 0 Solve the mutually recursive equations: Aᵢ = ∑ {σAⱼ : qⱼ ∈ Δ(qᵢ, σ), σ ∈ Σ} + {ε : if qᵢ ∈ F} Show this can be solved by a regular expression. 6/8/2021 Theory of Computation: Chapter 2 27

Arden’s fixed-point Lemma: Let A and B be any languages, such that ε ∉ A. Then the recursive equation X = AX + B has a unique solution X = A*B. Proof: Obviously A(A*B) + B = (A⁺ + ε)B = A*B is a solution. Clearly B ⊆ X, ⇒ AB ⊆ X ⇒ … ⇒ A*B ⊆ X means it is minimal. If a larger solution L existed, then C = L A*B ≠ ∅. Then A*B + C = A(A*B + C) + B = A⁺B + AC + B = A*B + AC. Now, C is disjoint from A*B, so (A*B + C) ∩ C = (A*B + AC) ∩ C ⇒ C = AC ∩ C ⇒ C ⊆ AC. Let x ∈ AC be of minimal length. Then x = yz, y ∈ A, z ∈ C. But ε ∉ A by hypothesis ⇒ z ∈ AC with |z| < |x|, contradiction. Note: The condition ε ∉ A is not a restriction because in a finite automaton, any epsilon loop from a state to itself can be removed. 6/8/2021 Theory of Computation: Chapter 2 28

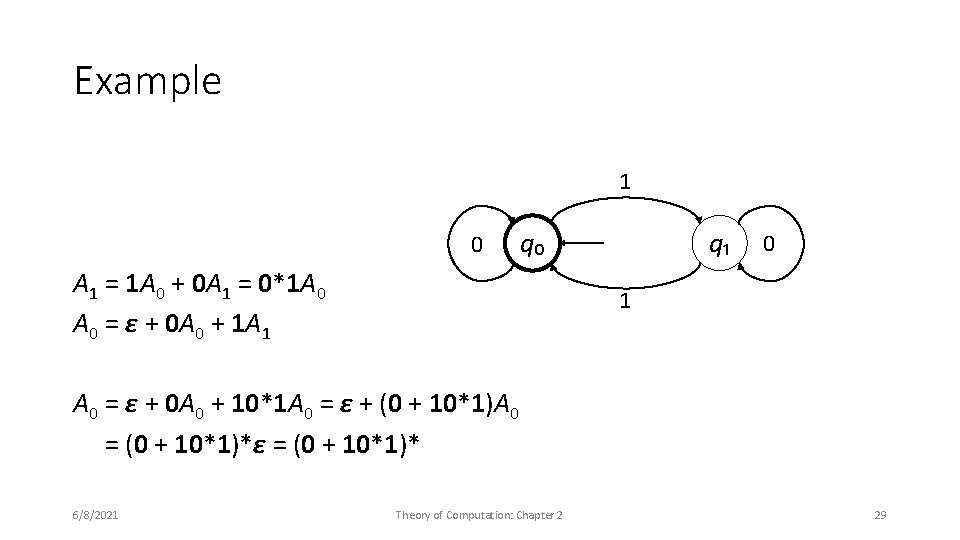
Example 1 0 q₀ A 1 = 1 A 0 + 0 A 1 = 0*1 A 0 = ε + 0 A 0 + 1 A 1 q₁ 0 1 A 0 = ε + 0 A 0 + 10*1 A 0 = ε + (0 + 10*1)A 0 = (0 + 10*1)*ε = (0 + 10*1)* 6/8/2021 Theory of Computation: Chapter 2 29

Solving sets of recursive equations Given a set of equations with numbered variables, start at the highest: Aᵢ = (A₀ … Aᵢ) use Arden to eliminate Aᵢ: Aᵢ = (A₀ … Aᵢ₋₁) Aᵢ₋₁ = (A₀ … Aᵢ) substitute for Aᵢ: Aᵢ₋₁ = (A₀ … Aᵢ₋₁) � Aⱼ = (A₀ … Aⱼ) use Arden to eliminate Aⱼ: Aⱼ = (A₀ … Aⱼ₋₁) Aⱼ₋₁ = (A₀ … Aᵢ) repeated substitution Aᵢ … Aⱼ: Aⱼ₋₁ = (A₀ … Aⱼ₋₁) � A₀ = (A₀) use Arden to eliminate A₀: A₀ = () solved! 6/8/2021 Theory of Computation: Chapter 2 31

Are all languages regular? Is L = {aⁿbⁿ : n ≥ 0} a regular language? Why not? Can you prove it? Suppose a machine M accepted L. Consider a string in L long enough to cause state repetition. Find a string not in L that is also accepted by M. 6/8/2021 Theory of Computation: Chapter 2 32

The pumping lemma Theorem: Let L be an infinite regular language. Then there is an n such that for all w ∈ L with |w| ≥ n, w can be written as w = uvx with |v| ≥ 1 and |uv| ≤ n such that for all i ≥ 0, uvix ∈ L. Proof: Let L = LM for some DFA M with n states. Running M on w ∈ L with |w| ≥ n means it visits ≥ n + 1 states, so some state appears twice, in which case M accepts uvix for all i ≥ 0, making uv*x ⊆ L. Uses PHP: Temporally: state appears twice on the path from start to final Spatially: we must pass through a loop on the diagram 6/8/2021 Theory of Computation: Chapter 2 33

Showing a language is not regular Take an infinite language L, assume it is regular toward a contradiction: ∀n, ∃w ∈ L, |w| ≥ n, so ∀uvx = w, |uv| ≤ n & v ≠ ε, ∃i ≥ 0 with uvⁱx ∉ L. Example: Suppose L = {ambm : m ≥ 0} is regular. Given any n, take w = aⁿbⁿ. Since w = uvx with |uv| ≤ n and |v| ≥ 1, v ∈ a⁺. Choose i = 0, to get uv⁰x = an−|v|bn ∉ L. Contradiction to the pumping lemma. Example: Suppose L = {0 i² : i ≥ 1} is regular. Take w = 0 n² = uvx, with 1 ≤ |v| ≤ n. So uv²x = 0 n²+|v|, but n² + |v| < (n + 1)2 = n² + 2 n + 1. Hence uv²x ∉ L. This contradicts the PL. 6/8/2021 Theory of Computation: Chapter 2 34

Explanation of pumping lemma Idea: If an infinite language L is regular, it must satisfy the property: PL: ∃n ∀w ∈ L ∃uvx = w |w| ≥ n ¬PL: ∀n ∀i ≥ 0 uvⁱx ∈ L |v| ≥ 1 |uv| ≤ n ∃w ∈ L ∀uvx = w ∃i ≥ 0 uvⁱx ∉ L i. e. if an infinite L doesn’t satisfy the property, then it can’t be regular. 6/8/2021 Theory of Computation: Chapter 2 35

Using closure properties Intersection can show irregularity, together with the pumping lemma: Example: {ww. R : w ∈ {a, b}*} ∩ a*bba* = {aⁿb²aⁿ : n ≥ 0} which is easy to show irregular by the PL. Therefore, {ww. R : w ∈ {a, b}*} is irregular. 6/8/2021 Theory of Computation: Chapter 2 36

Deciding emptiness and infinitude (machines) Suppose L is given by a finite automaton M (without ε transitions) with start state s ∈ Q and final states F ⊆ Q. Let → be the DAG of M in which transition labels are ignored. Then the following problems are decidable: LM ≠ ∅ ⇔ |LM| = ∞ ⇔ s →* f ∈ F s →* q →⁺ q →* f ∈ F for some q ∈ Q Equivalence: L₁ = L₂ iff (L₁ ⊆ L₂ and L₂ ⊆ L₁) ⇔ (L₁ ∪ L₂) ∖ (L₁ ∩ L₂) = ∅. 6/8/2021 Theory of Computation: Chapter 2 37

Simplifying regular expressions Fact: If we let the multiplicative identity ∅* = ε, then every non-empty regular expression can be written without the use of the empty set. Reason: Remove ∅ bottom-up from every sub-expression, except ∅*. Fact: Every regular language not containing the empty string can be written without the use of ε. Reason: Remove ∅* top-down from every sub-expression without ε. Fact: Once these exceptional cases are removed, a regular expression denotes an infinite language iff it contains a Kleene star (*). Example: 6/8/2021 Theory of Computation: Chapter 2 38