Chapter Three Quantum Theory the Structure of the

Chapter Three Quantum Theory & the Structure of the Atom

Objectives/Goals for Today Discuss logistics of graded assignments Quiz over Chapter 2 Chapter three notes Section 3. 1 Section 3. 2 Section 3. 3 Section 3. 4 Section 3. 5 Section 3. 6 Section 3. 7 Section 3. 8 Section 3. 9 Section 3. 10

Section 3. 1 Energy & Types of Energy

Energy Types of Energy: Kinetic-Energy due to motion Thermal Potential-Energy due to position/arrangement Gravitational Chemical Electrostatic Energy is measured in Joules (J); N*m; kg*m/s 2

Section 3. 2 The Nature of Light

A slight history of the atom Last time in Chemistry… Atoms had protons, neutrons, & electrons Protons and neutrons in dense core called nucleus Electrons orbit nucleus (provide most of volume) The atom was assumed to look a little bit like a microscopic solar system

A Traditional View of the Atom

Newton, we have a problem… Classical descriptions: ◦ Dalton: atoms are hard particles, all atoms of the same element are the same ◦ Energy is continuous ◦ Planetary model of atom ◦ Newtonian laws (macroscopic) were not working for atomic behavior (microscopic)

Some Observations… New view of atomic behavior ◦ Blackbody Radiation—Max Planck: heat solids to red or white heat, matter did not emit energy continuously; in whole-number multiples of certain quantities ◦ Matter absorbs or emits energies in packets - quanta

Some More Observations: The Photoelectric Effect—Albert Einstein: used Planck’s theory to observe metals reacting to different colors of light –electrons are ejected from the surface of certain metals exposed to light at a certain minimum frequency Blue light (n = 6. 7 x 1014 Hz) causes Na to emit electrons, red light (n = 4. 0 x 1014 Hz) does not Energy of electrons dependent solely on frequency, not light intensity

What’s Going on Inside the Atom? Scientists began studying the structure and composition of individual atoms. They used substances’ interactions with light to explain the structure of atoms and develop a model to explain how atoms affected properties of light. In order to understand interactions, we must understand behavior of light.

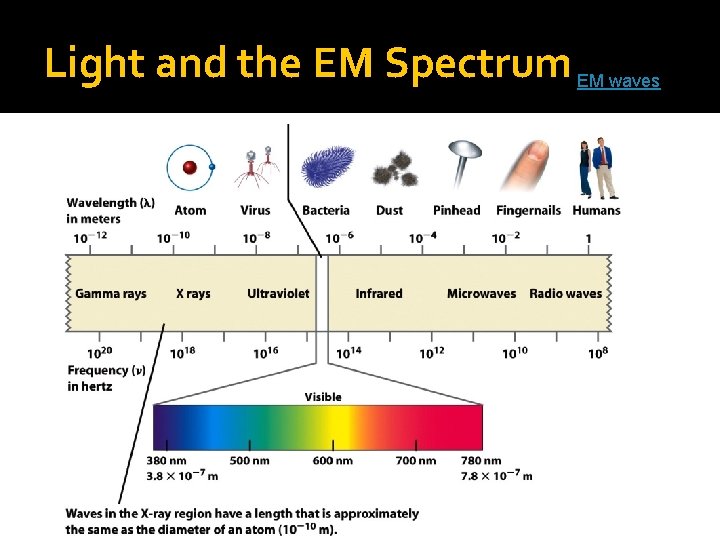
Light is typically described as traveling in waves (similar to water); All electromagnetic (EM) waves (including visible light) are made of two components: electric and magnetic ALL EM waves travel at the speed of light, c (2. 998 x 10 8) c = ln (Know these!) c = speed of light; l (lambda) = wavelength (m, nm); n (nu) = frequency (1/s, s-1, Hz)

Light and the EM Spectrum EM waves

EM Spectrum Different colors of light correspond to different wavelengths in the visible portion of the EM spectrum. Two wavelengths (l) are shown below. Determine the frequency (n) for each wave. Blue light Red light 1 nm = 1 x 10 -9 m OR 1 x 109 nm = 1 m

Double Slit Experiment From the many experiments about light, light exhibits wave and particle properties Double Slit Experiment

Section 3. 3 Quantum Theory

From Classical to Quantum Theory Quantum has come to mean small; originated from Planck’s observation of quantized energy New set of “rules” had to be used for the subatomic world

Wave-Particle Duality Based on photoelectric effect, light acts as a wave but also exists as a stream of particles called photons Energy of photons is proportional to frequency, inversely proportional to wavelength h = 6. 626 x 10 -34 J • s J = kg • m 2 / s 2

Calculation Practice c = ln; E = hn 1) Which has a higher frequency: light from a red stoplight with a wavelength of 750 nm or a yellow light with a wavelength of 600 nm? 2) What is the wavelength of a radio station’s waves transmitting at a frequency of 101. 5 MHz (megahertz)? (FM radio waves range from 30 – 300 MHz. ) 3) Red lights at traffic stops have wavelengths of about 650 nm. What is the frequency (in Hz) of this light? 4) Calculate the energy (in Joules) of a photon with a wavelength of 5. 00 x 104 nm (infrared region). Answers: yellow, 2. 956 m, 4. 62 x 1014 Hz, 3. 98 x 10 -21 J

Beginning of Quantum Theory Video

Section 3. 4 Bohr’s Theory of the Hydrogen Atom

The Problem… As electrons orbit, they radiate energy (due to acceleration) If electrons radiate energy, they must eventually start spiraling towards nucleus Electron would eventually hit the nucleus where the proton is and the atom would annihilate itself This doesn’t happen…whew!

The Solution… Neils Bohr proposed the idea that electrons orbit the nucleus in FIXED orbits

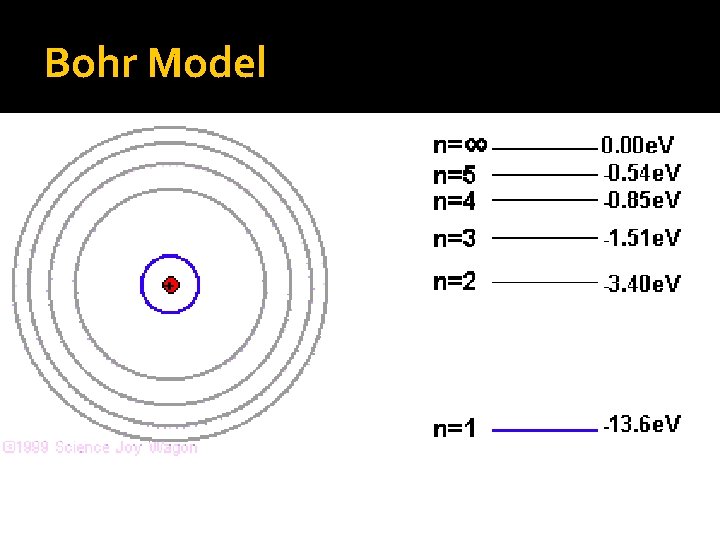
Bohr’s Model of the Atom Electrons travel in discrete, quantized circular orbits; like going up or down stairs. Each orbit has a specific energy associated with it, labeled as n = 1, 2, etc. Ground state is the lowest energy level for an atom (n = 1).

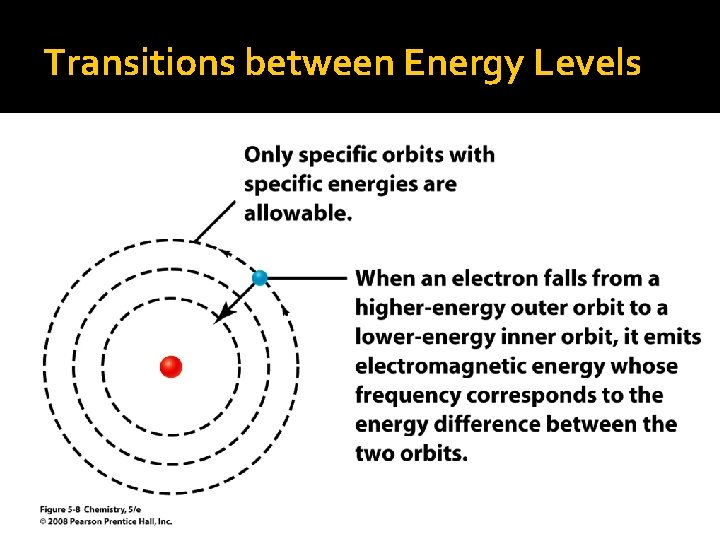
Electrons Jumping Electrons CANNOT exist in BETWEEN orbits If an electron is to “jump” orbits (move away from the nucleus), it needs to ABSORB energy in just the right quantity If an electron is to “drop” orbits (move closer to the nucleus), it will RELEASE energy in the form of electromagnetic radiation Sometimes visible light, sometimes not

Bohr’s Model of the Atom

Bohr Model The Hydrogen Atom

Transitions between Energy Levels

Visible Light White light we see consists of all colors in the visible spectrum. Use a prism (or CD) to break them up. Light given off by atoms doesn’t necessarily correspond to all visible colors.

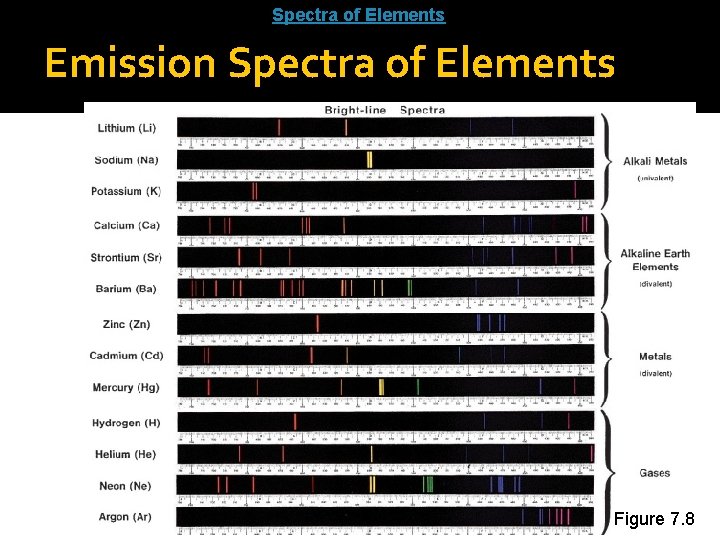
Emission Spectra Hydrogen Each element gives off unique spectrum Tubes Each element has its own individual emission spectrum. This allowed scientists to identify elements in different minerals.

Spectra of Elements: http: //www. wwnorton. com/college/chemistry/chemconnections/Blue. Light/pages/elements. html Emission Spectra of Elements Figure 7. 8

Section 3. 5 Wave Properties of Matter

Another Problem… Bohr stated that electrons move in FIXED orbits. But why? ? ?

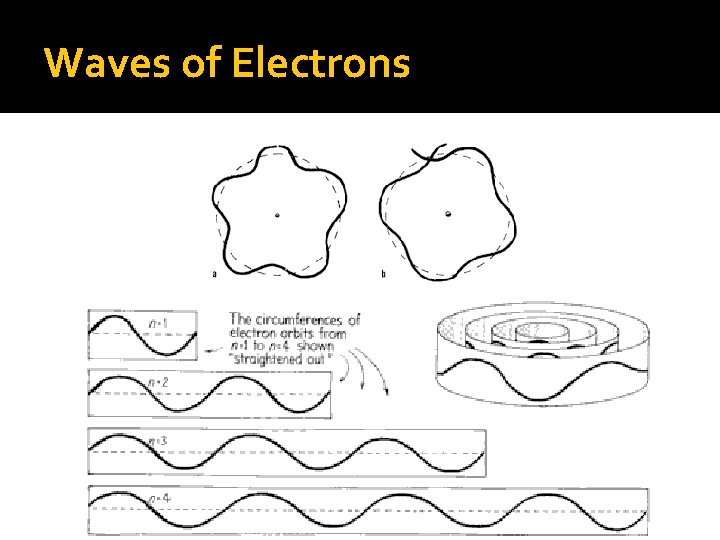
Wavelike Properties of Matter de Broglie: If light can behave like a wave and a particle, then matter (i. e. , electrons) can behave like a wave If an electron behaves like a standing wave, then it can only have specific wavelengths Can calculate wavelength for matter if we know its velocity (use v instead of c): l = h / m v (This is the de Broglie equation. ) h = Planck’s constant, m = mass (electron’s have constant mass: 9. 11 x 10 -31 kg), v = velocity (speed)

Waves of Electrons

Group Quiz #1 1) The energy of a photon is 5. 87 x 10 -20 J. What is the frequency of the photon? 2) What is the wavelength of an electron that travels at 34. 7 m/s and has a mass of 9. 11 x 10 -31 kg? 3) A 0. 143 kg baseball is thrown at a velocity of 42. 5 m/s. Calculate the wavelength of the baseball. How does the baseball’s wavelength compare to the electron from the example above?

Group Quiz #2 4) Calculate the energy of a photon that has a wavelength of 35. 6 nm (in the x-ray region). (Hint: Watch units!!!)

Section 3. 6 Quantum Mechanics

Heisenberg Uncertainty Principle If electrons have wave-like properties and particle-like, then we can’t know both its position and velocity (momentum) at the same time In order to determine the position of an electron, we hit it with a photon of light, but this will change its position and velocity.

Quantum Mechanical Model The Bohr model worked well for hydrogen, but failed for elements with more than one proton and one electron. Quantum Mechanics was developed (by Schrödinger in the 1920’s) to describe the motion of subatomic particles Did not attempt to describe exact position of particles; used mathematical equations to describe the probability of finding the particles The probability density (map of likely locations) is the “electron cloud”

Atomic Orbitals (NOT ORBITS) The region of highest probability for finding an electron is an “electron cloud”. This region of high probability is also called an atomic orbital. Each orbital holds at most 2 electrons. 41

Section 3. 7 Quantum Numbers

Quantum Numbers There are 4 quantum number that help describe the orbitals for electrons We use these numbers to describe where electrons are most likely to be found for an atom. Can also use the periodic table!!! 43

Four Quantum “Numbers” n l ms

The Principal Quantum Number The Principal Quantum Number, n describes distance of the electron from the nucleus; called shells n = 1, 2, 3, etc; larger number is farther from nucleus n corresponds to a row in the periodic table

The Next Quantum Number The Angular Momentum Quantum Number, l In the periodic table are different groups of orbitals with different shapes. These groups of orbitals are called subshells and labeled s (0), p (1), d (2), and f (3). s subshells are spherical (first two columns) p subshells are dumb-bell shaped (last six columns) d subshells are intersecting dumb-bells (transition metals) f subshells are lanthanides/actinides 46

The Last Two Quantum Numbers The Magnetic Quantum Number, ml describes the orientation of the orbital with respect to x, y, and z axes s, p, and d orbitals have different shapes and therefore different orientations The Spin Quantum Number, ms describes the spin of an electron in an orbital (shown as up and down arrows in orbital diagrams)

Section 3. 8 Atomic Orbitals

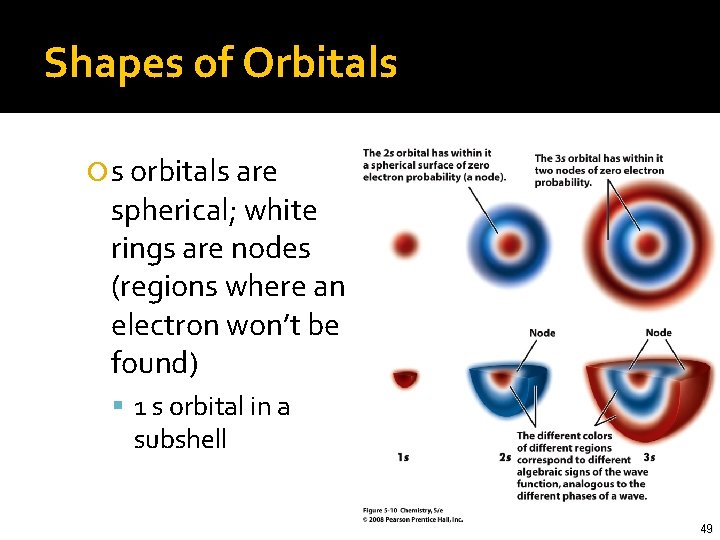
Shapes of Orbitals s orbitals are spherical; white rings are nodes (regions where an electron won’t be found) 1 s orbital in a subshell 49

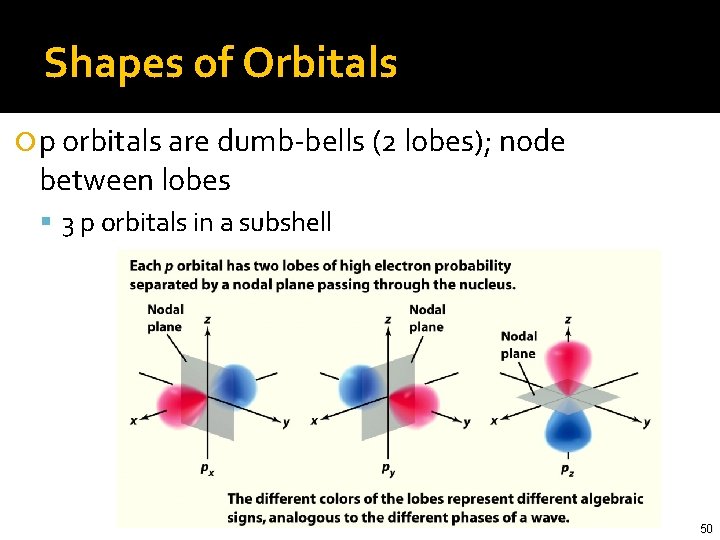
Shapes of Orbitals 2 px orbital 2 py orbital 2 pz orbital p orbitals are dumb-bells (2 lobes); node between lobes 3 p orbitals in a subshell 50

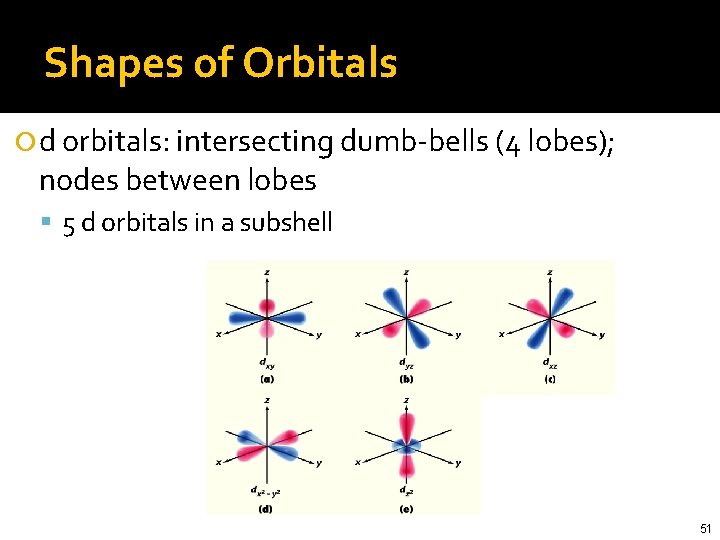
Shapes of Orbitals d orbitals: intersecting dumb-bells (4 lobes); nodes between lobes 5 d orbitals in a subshell 51

Orbitals of Scandium

Shells and Subshells The first shell (row) has 1 subshell (s) s only 1 orbital An s subshell can hold at most 2 electrons The 2 nd shell (row) has 2 subshells (s and p) p set of 3 orbitals A p subshell can hold at most 6 electrons, 2 per orbital The 3 rd shell (row) has 3 subshells (s, p, and d) d set of 5 orbitals A d subshell can hold at most ? electrons The 4 th shell (row) has 4 subshells (s, p, d, and f) f set of 7 orbitals What is the maximum number of electrons allowed in the f subshell? 53

Section 3. 9 & 3. 10 Electron Configurations

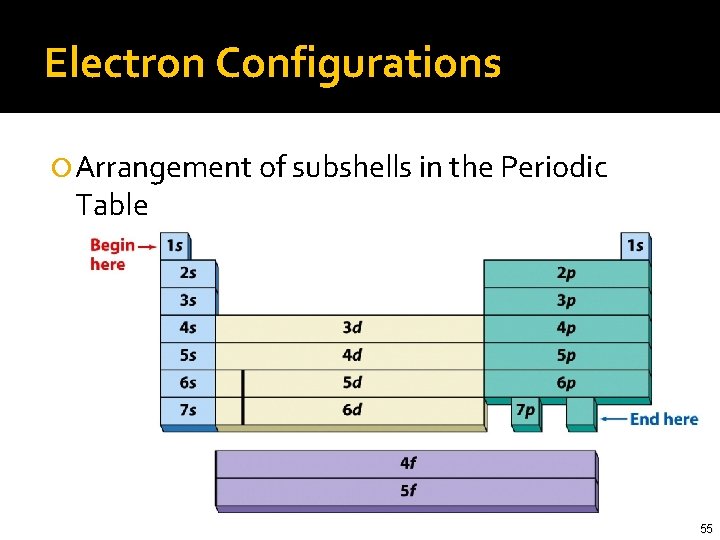
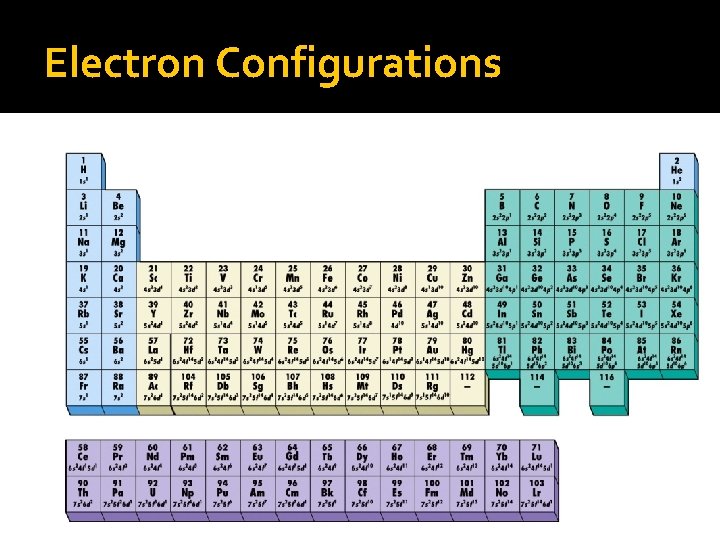
Electron Configurations Arrangement of subshells in the Periodic Table 55

Things that make you go hmmm…. What is the maximum number of: electrons allowed in the 2 px orbital? subshells allowed in the 4 th shell? electrons allowed in the 3 d subshell? electrons allowed in the 4 d subshell? electrons allowed in the 3 p subshell? electrons allowed in the 3 rd shell?

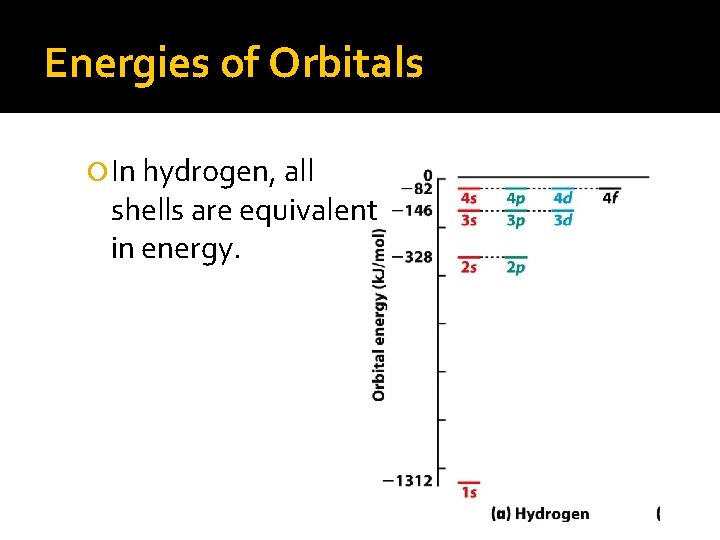
Energies of Orbitals In hydrogen, all shells are equivalent in energy.

Energies of Orbitals In many-electron models, the energy levels depend on the shell and subshell.

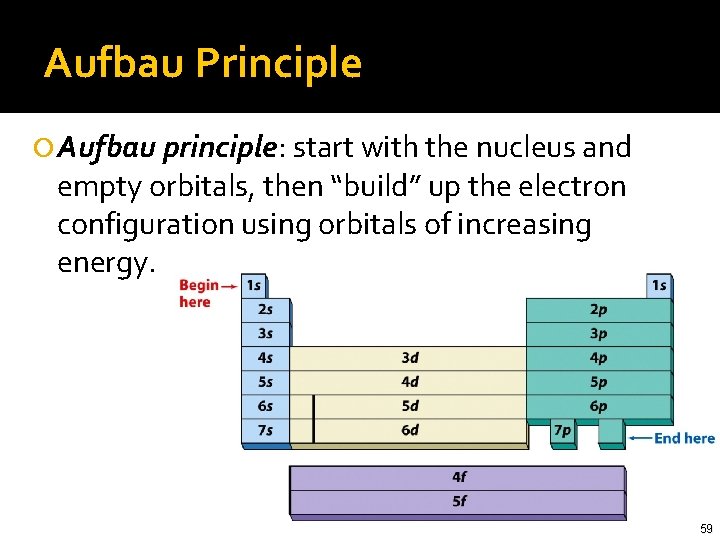
Aufbau Principle Aufbau principle: start with the nucleus and empty orbitals, then “build” up the electron configuration using orbitals of increasing energy. 59

Electron Configurations Arrangement of subshells in the Periodic Table 60

Electron Configurations Arrangement of subshells in the Periodic Table 61

Electron Configurations Arrangement of subshells in the Periodic Table 62

Electron Configurations Arrangement of subshells in the Periodic Table 63

Electron Configurations Arrangement of subshells in the Periodic Table 64

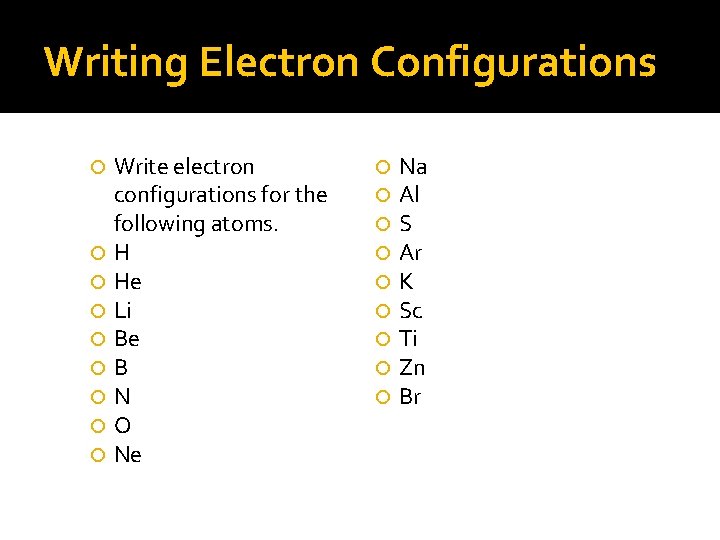
Writing Electron Configurations Write electron configurations for the following atoms. H He Li Be B N O Ne Na Al S Ar K Sc Ti Zn Br

Electron Configurations

Valence Electrons in the outermost shell. 1 s 2 2 s 2 2 p 6 3 s 2 3 p 5 Identify the number of valence electrons (v. e. ) in the following configurations: 1 s 2 2 p 6 3 s 2 1 s 2 2 p 33 s 2 1 s 2 2 s 2 67

Shorthand Notation Rather than writing out complete electron configurations, we can use the previously filled shell (noble gas) and show the valence electrons (v. e. ): P: 1 s 2 2 p 6 3 s 2 3 p 3 [Ne] 3 s 2 3 p 3 (5 v. e. ) Write the shorthand notation for: Ca Cl Sr Fe

Electron Configuration Some exceptions to the Aufbau order… What are the expected electron configurations for Cr and Cu? Filled and half-filled d subshells seem to be especially stable. Cr: 1 s 2 2 p 6 3 s 2 3 p 6 4 s 1 3 d 5 Also true for Mo and W Cu: 1 s 2 2 p 6 3 s 2 3 p 6 4 s 1 3 d 10 Also true for Ag and Au 69

Hund’s Rule If two or more orbitals (i. e. , a p orbital) with the same energy are available, one electron goes into each orbital until they have to pair up. Fighting siblings For example, an atom with 2 p electrons: 1 electron will go into the first (px) orbital, the next electron will go into the second (py) orbital.

Pauli Exclusion Principle Pauli Exclusion Principle: no two electrons can have the same values of all 4 quantum numbers Describes what happens when electrons share an orbital. Only two electrons can occupy a single orbital and they must have opposite spin (i. e. , the 4 th quantum number). The first electron is designated as positive spin (up arrow), the second electron in that orbital has negative spin (down arrow). 71

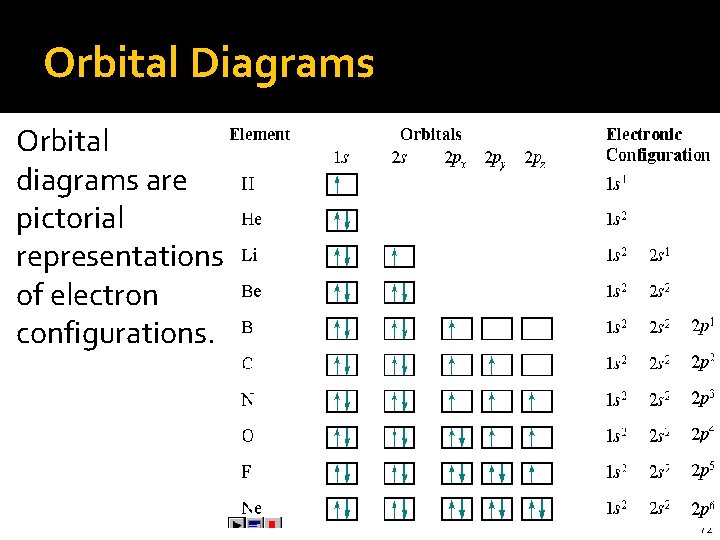
Orbital Diagrams Orbital diagrams are pictorial representations of electron configurations. 72

Group Quiz #3 Write electron configurations for the following elements (long-hand notation). Indicate the number of v. e. for each element. potassium sulfur carbon magnesium lithium