Chapter Three Baseband DemodulationDetection Dept of EE NDHU

Chapter Three Baseband Demodulation/Detection Dept. of EE, NDHU 1

Error Probability Performance • Error probability function where r is the time cross-correlation coefficient between two signals • Antitpodal signal – r equals to -1, then • Orthogonal signal – r equals to 0, then Dept. of EE, NDHU 2

Error Probability of Binary Signaling • Unipolar signaling • Detection of unipolar baseband signaling Dept. of EE, NDHU 3

Error Probability of Binary Signaling • Bipolar signaling • Detection of bipolar baseband signaling Dept. of EE, NDHU 4
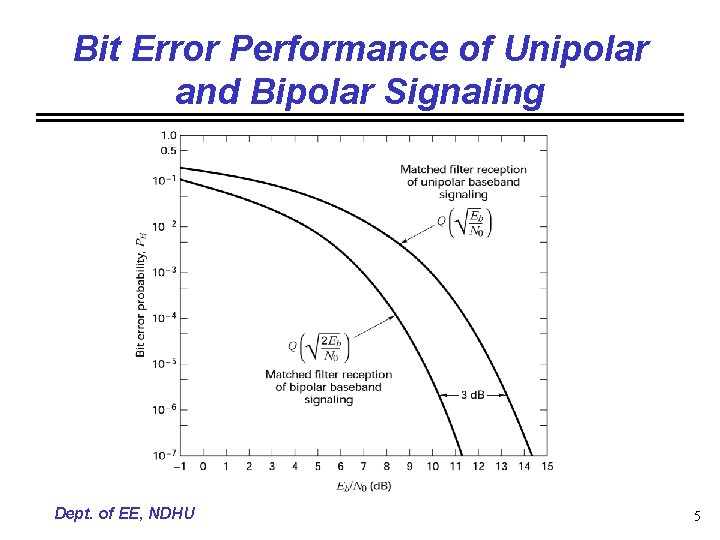
Bit Error Performance of Unipolar and Bipolar Signaling Dept. of EE, NDHU 5
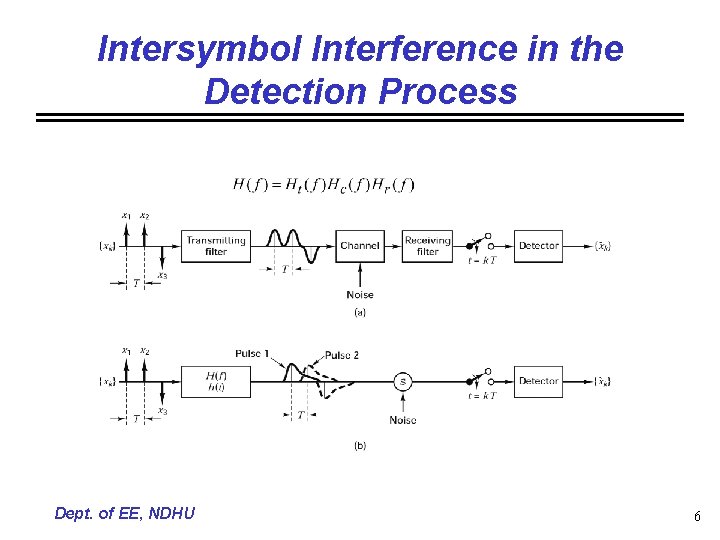
Intersymbol Interference in the Detection Process Dept. of EE, NDHU 6
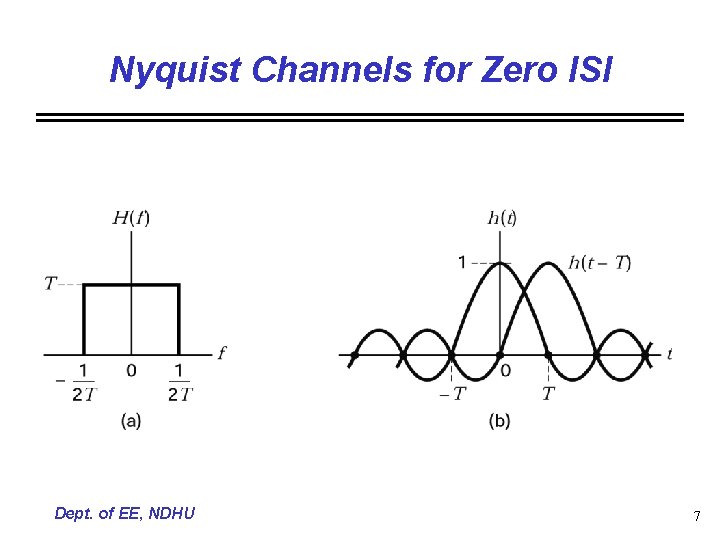
Nyquist Channels for Zero ISI Dept. of EE, NDHU 7

Pulse Shaping to Reduce ISI • Goals and Trade-offs – Compact signaling spectrum is to provide the higher allowable data rate – Time pulse would become spread in time, which induces ISI • The Raised-Cosine filter where W is the absolute bandwidth and W 0=1/2 T represents the minimum Nyquist bandwidth and the -6 d. B bandwidth Dept. of EE, NDHU 8
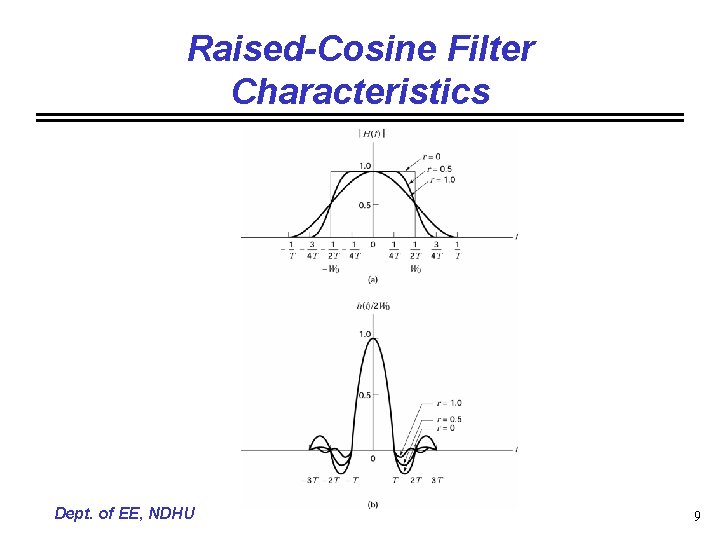
Raised-Cosine Filter Characteristics Dept. of EE, NDHU 9
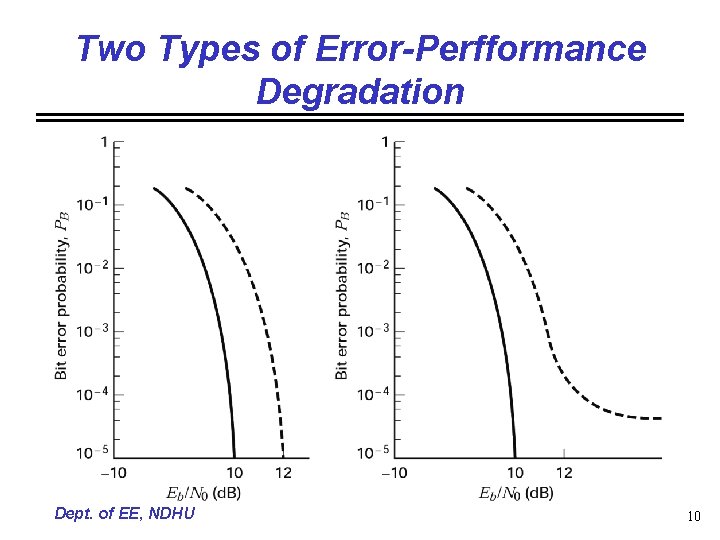
Two Types of Error-Perfformance Degradation Dept. of EE, NDHU 10

Example 3. 3 Bandwidth Requirements (a) Find the minimum required bandwidth for the baseband transmission of a four-level PAM pulse sequence having a data rate of R=2400 bits/s if the system transfer characteristic consists of a raised-cosine spectrum with 100% excess bandwidth (r=1) (b) The same 4 -ary PAM sequence is modulated onto a carrier wave, so that the baseband spectrum is shifted and centered at frequency f 0. Find the minimum required DSB bandwidth for transmitting the modulated PAM sequence Dept. of EE, NDHU 11
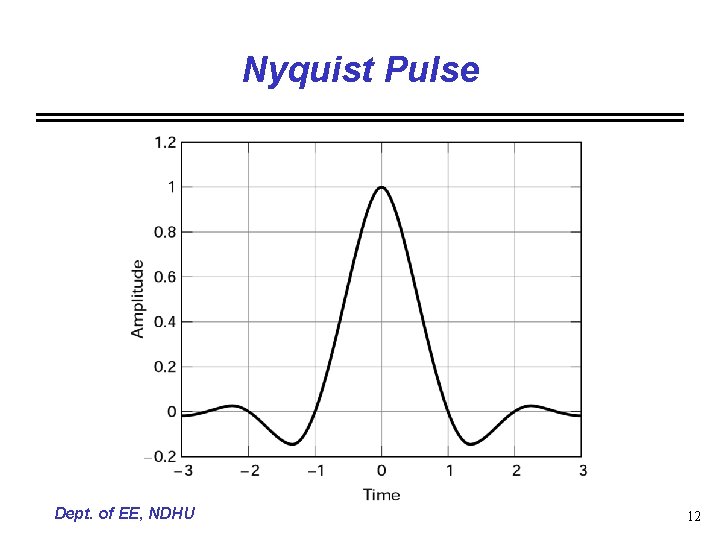
Nyquist Pulse Dept. of EE, NDHU 12
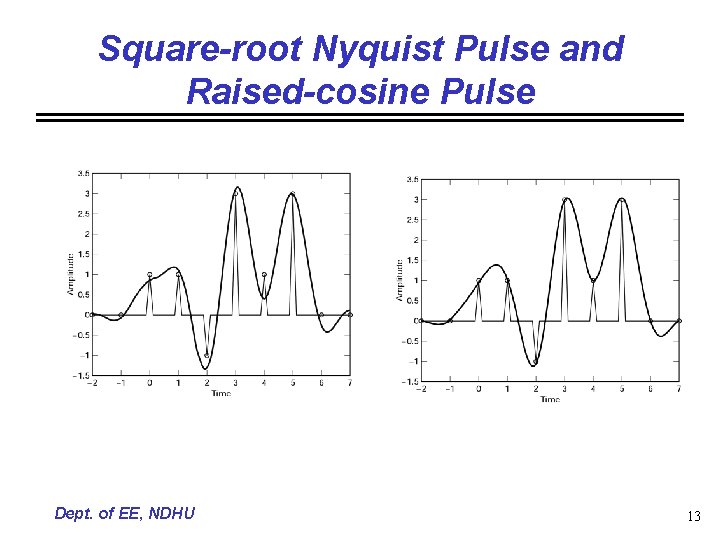
Square-root Nyquist Pulse and Raised-cosine Pulse Dept. of EE, NDHU 13

Equalization • Maximum-likelihood sequence estimation (MLSE) – Make measurement of channel response and adjust the receiver to the transmission environment – Enable the detector to make good estimates from the distorted pulse sequence (ex. Viterbi equalization) • Equalization with filtering – Use filter to compensate the distorted pulse – Linear filter contains only feedforward elements (ex. transversal equalizers) – Non-linear filter contains both feedforward and feedback elements (ex. decision feedback equalizers) – Preset or adaptive filter design – Filter’s resolution and update rate Dept. of EE, NDHU 14

Receiving / Equalizing Filter • The overall transfer function • System design goal then Ht(f) and Hr(f) each have frequency transfer functions that are the square root of the raised cosine. • Equalizing filter sometimes not only compensates the channel effect but compensates the ISI brought by the transmitter and receiver (ex. Gaussian filter) Dept. of EE, NDHU 15
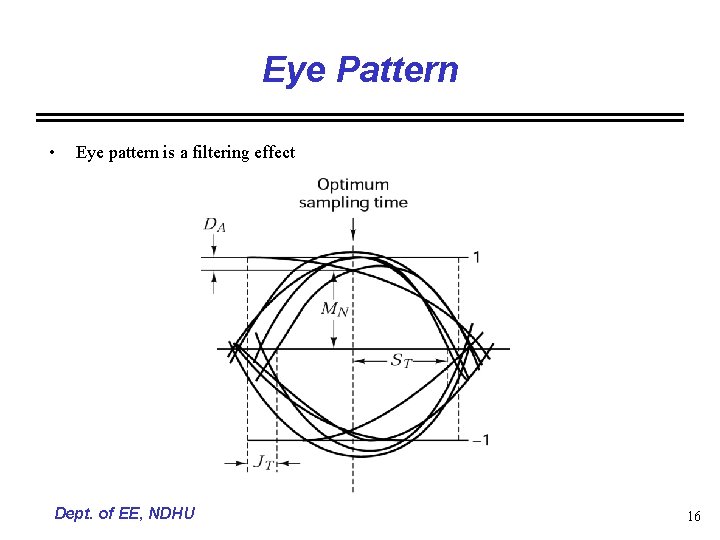
Eye Pattern • Eye pattern is a filtering effect Dept. of EE, NDHU 16
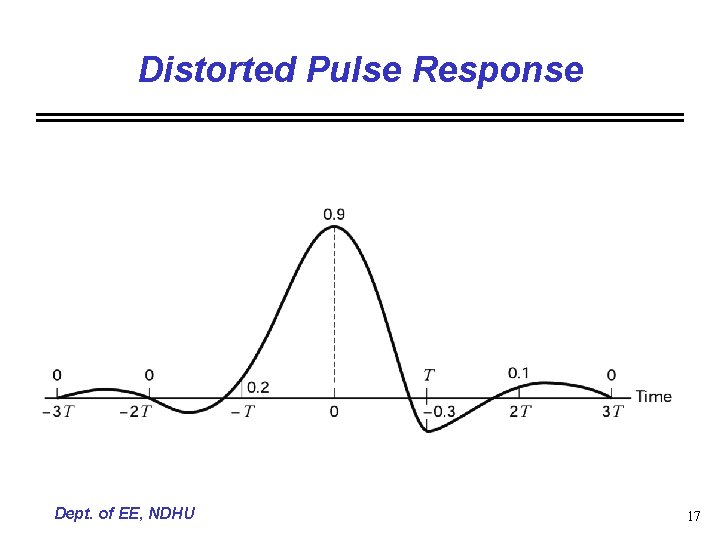
Distorted Pulse Response Dept. of EE, NDHU 17

Transversal Equalizer • A training sequence (like PN sequence) is needed to estimate the channel frequency response • A transversal filter is the most popular form of an easily adjustable equalizing filter consisting of a delay line with T-second tapes • The main contribution is from a central tap of a transversal filter • In practice, a finite-length transversal filter is realized to approximate the ideal filter (infinite-length transversal filter) • Consider there are (2 N+1) taps with weights c-N, c-N+1, …, c. N, the equalizer output samples {z(k)} Dept. of EE, NDHU 18
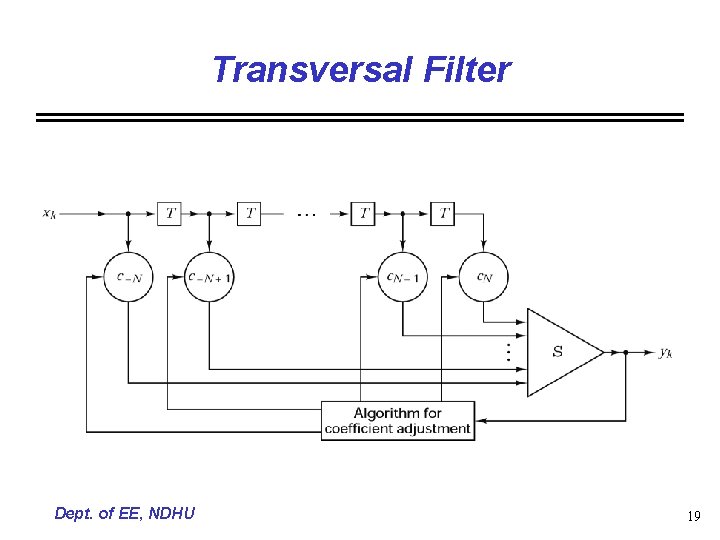
Transversal Filter Dept. of EE, NDHU 19

Zero-Forcing Solution • Relationship among {z(k)}, {x(k)}, and {cn} for the transversal filter • Disposing the top N the bottom N rows of the matrix X into a square matrix with dimension of 2 N+1 and transform Z vector into a vector of 2 N+1 • Rewrite the relationship • Select the weights {cn} so that the equalizer output is Dept. of EE, NDHU 20

Example: A Zero-Forcing Equalizer • Consider a three-taps transversal filter, the given received data {x(k)} are 0. 0, 0. 2, 0. 9, -0. 3, 0. 1. Using the zero-forcing solution to find the weights {c-1, c 0, c 1} – For the relationship Dept. of EE, NDHU 21

Minimum MSE Solution • Minimize the mean-square error (MSE) of all the ISI terms plus the noise power at the output of the equalizer • MSE is defined as the expected value of the squared difference between the desired data symbol and the estimated data symbol • MSE solution • Minimum MSE solution is superior to zero-forcing solution • Minimum MSE is more robust in the presence of noise and large ISI Dept. of EE, NDHU 22

Decision Feedback Equalizer • Limitation of a linear equalizer is that it performs poor on channel having spectral nulls • Decision feedback equalizer (DFE) is a non-linear equalizer and uses previous detector decisions to eliminate the ISI on pulse • Basic idea is that if the values of the symbols previously detected are known, then the ISI contributed by these symbols can be cancelled out • Forward filter and feedback filter are used in the DFE • The advantage of DFE is that the feedback filter operates on noiseless quantized levels, and thus its output is free of channel noise Dept. of EE, NDHU 23
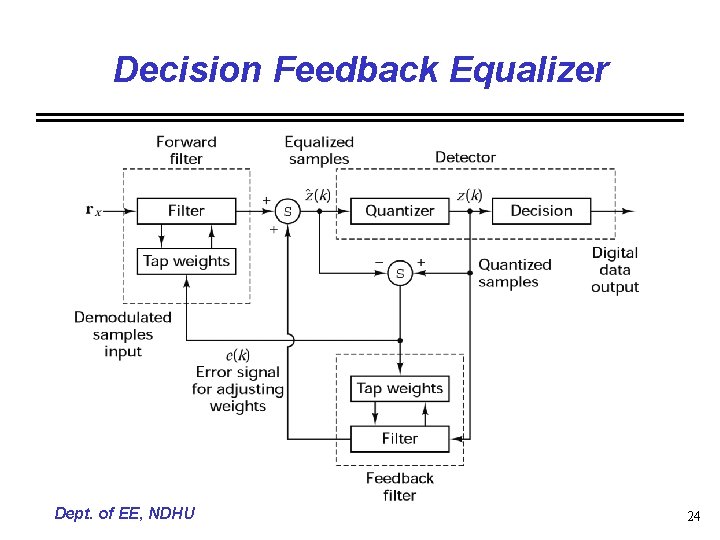
Decision Feedback Equalizer Dept. of EE, NDHU 24

Preset and Adaptive Equalization • The equalizer weights remain fixed during transmission of data, then the equalization is called preset equalization • Preset equalization sets the tap weights according to some average knowledge of the channel (Ex. Voice-grade telephone) • Adaptive equalization can be implemented to perform tap-weight adjustments periodically or continually • Periodic adjustments are accomplished by periodically transmitting a preamble sequence • Continually adjustment are performed by the decision directed procedure Dept. of EE, NDHU 25

Preset and Adaptive Equalization • • Disadvantages of preset equalization – Require an initial training period – A time-varying channel can degrade system performance If the probability of error exceeds one percent (rule of thumb), decision-directed adaptive equalizer might not converge • Common solution to the adaptive equalization – Initialize the equalizer with a preamble to provide good channel-error performance – Then switch to the decision-directed mode – Blind equalization algorithm can be used to form initial channel estimates without a preamble Dept. of EE, NDHU 26
- Slides: 26