Chapter One What Is Logical Thinking And Why

Chapter One What Is Logical Thinking? And Why Should We Care? Copyright © 2012 Pearson Education, Inc. All rights reserved.

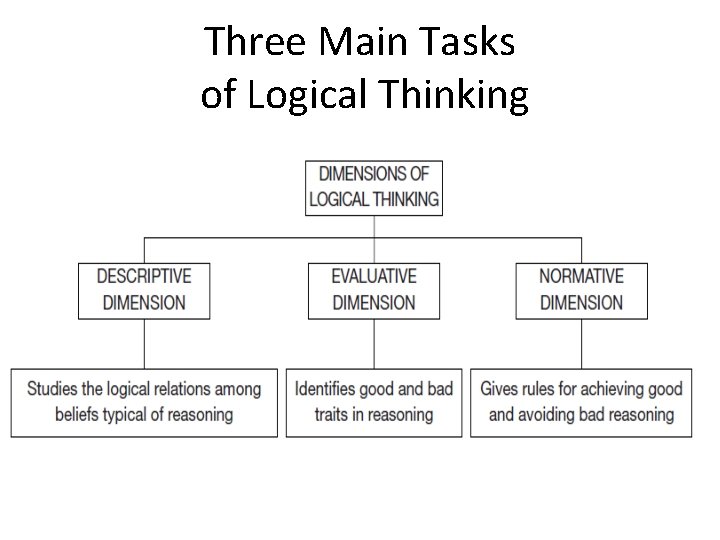
The Study of Reasoning • Logical thinking, or informal logic, is a branch of philosophy devoted to the study of reasoning. • Reasoning consists in logical relations. – One of the chief logical relations is the inference or argument. – In an inference or argument, the thinker entertains one or more beliefs as reasons in support of another belief. Copyright © 2012 Pearson Education, Inc. All rights reserved.

The Goals of Logical Thinking • To have true beliefs and avoid false ones. • To upgrade the set of beliefs we already have by acquiring new true beliefs and avoiding false ones. Copyright © 2012 Pearson Education, Inc. All rights reserved.

Strength of Inferences • An inference can be strong, weak, or failed. This is the central concept in logical thinking. • Example of a strong inference: – All whales are mammals, and Moby Dick is a whale; therefore, Moby Dick is a mammal. • Example of a weak inference: – No oranges from Florida are small; therefore, no oranges from the United States are small. • Example of a failed inference: – No oranges are apples; therefore all elms are trees. Copyright © 2012 Pearson Education, Inc. All rights reserved.

Three Main Tasks of Logical Thinking Copyright © 2012 Pearson Education, Inc. All rights reserved.

Formal vs. Informal Logic • Formal logic (or symbolic logic) uses a symbolic notation to deduce theorems from formulas. Formal logic is not concerned with the inferences people actually make in ordinary reasoning. • Informal logic is completely focused on the study of logical relations as they occur when ordinary reasoning is at work. Copyright © 2012 Pearson Education, Inc. All rights reserved.

Practical Uses of Logical Thinking Copyright © 2012 Pearson Education, Inc. All rights reserved.

What are Arguments? • Argument = the relation whereby one or more statements are offered in support of another statement. – Every argument must consist of at least two statements, one that makes a claim of some sort (conclusion), and one or more others that are offered in support of it (premise). Copyright © 2012 Pearson Education, Inc. All rights reserved.

The Building Blocks of Argument Copyright © 2012 Pearson Education, Inc. All rights reserved.

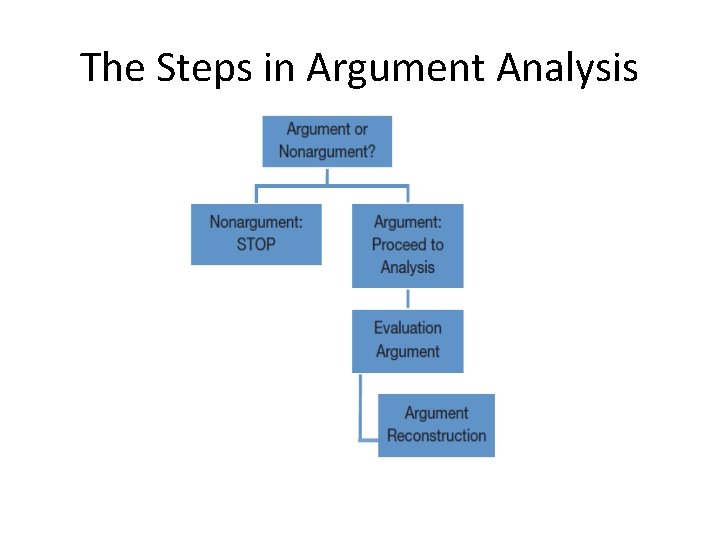
Analyzing Arguments • In order to analyze arguments you must be able to: – Recognize arguments. – Identify the logical relation between their parts. – Evaluate arguments. Copyright © 2012 Pearson Education, Inc. All rights reserved.

The Steps in Argument Analysis Copyright © 2012 Pearson Education, Inc. All rights reserved.

Reconstructing Arguments • Form for reconstructing arguments: – List the premises first and give each a number. – Draw a horizontal line after the last premise. – List the conclusion last and give it a number. • An example: 1. All lawyers are attorneys. 2. Jack Mc. Coy is a lawyer. __________________________________________ 3. Jack Mc. Coy is an attorney. Copyright © 2012 Pearson Education, Inc. All rights reserved.

Premise and Conclusion Indicators • In order to properly reconstruct an argument, you must be able to properly identify the premises and conclusion in a particular argument. • The following are words that indicate a premise: – because, since, for, given that, assuming that, provided that, as, whereas, after all, for the reason that, inasmuch as, in that, follows from, is a consequence of, considering that • The following words indicate a conclusion: – therefore, hence, so, entails that, suggest that, accordingly, supports that, consequently, from this we can see that, we may conclude that, we may infer that, it follows that, thus, recommends that, for this reason, as a result Copyright © 2012 Pearson Education, Inc. All rights reserved.

Identifying Premises and Conclusions • The premise and conclusion indicators are helpful for identifying premises and conclusions, but they are not foolproof. • In some arguments, words that are common indicators may not signal a premise or conclusion. • In other arguments, there may not be any indicators at all. • Remember, the most reliable way to identify premises and conclusions is to ask yourself: (1) what is the claim being made (that will be your conclusion) and (2) which statements are being made in support of the claim being made (those will be your premises). Copyright © 2012 Pearson Education, Inc. All rights reserved.

Arguments and Non-Arguments • An argument can be distinguished from other logical relations among statements chiefly by asking whether it offers some statements in support of a claim. If not, then it is not an argument. • Explanations often bear a superficial resemblance to arguments. Therefore, it is particularly important that the logical thinker be able to spot the difference between an argument and an explanation. Copyright © 2012 Pearson Education, Inc. All rights reserved.

Arguments vs. Explanations • In arguments, the reasons (premises) are offered to back up a claim (conclusion) that the arguer considers in need of support. • In explanations, reasons are offered to account for the events or states of affairs described by a claim that the arguer to be not in need of support. Copyright © 2012 Pearson Education, Inc. All rights reserved.

Conditionals • Conditionals are also commonly confused with arguments. – If … then statements are used to make compound statements called conditionals. • While conditionals may form a part of an argument, the conditional by itself is not an argument. Copyright © 2012 Pearson Education, Inc. All rights reserved.

Fictional Discourse • The truth value of statement-like sentences in fiction or poetry is ambiguous. • Therefore, any passage of fiction is nonargument. Copyright © 2012 Pearson Education, Inc. All rights reserved.