Chapter one Matrix Theory Background 1 Hermitian and

Chapter one Matrix Theory Background

1. Hermitian and real symmetric matrix

adj. A

Symmetric and Hermitian matrices n Symmetric matrix: n Hermitian matrix: n : Complex symmetric matrix

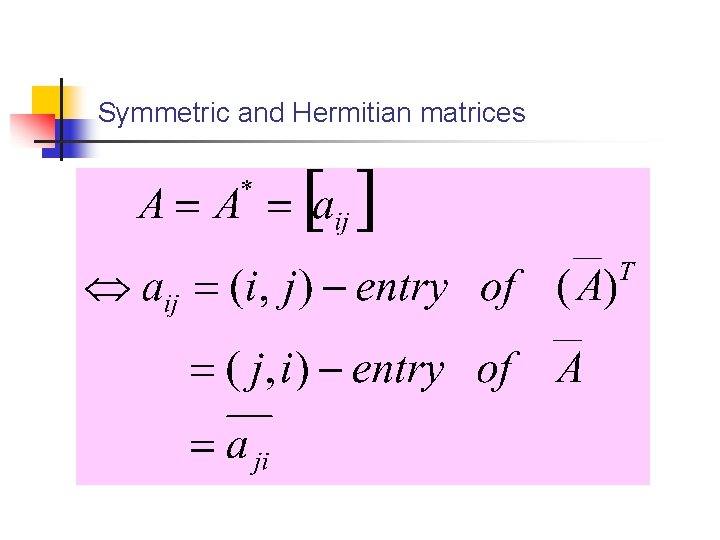
Symmetric and Hermitian matrices

Hermitian matrices

Hermitian matrices Form n Let H be a Hermitian matrix, then H is the following form conjugate compelx number

Skew-Symmetric and Skew- Hermitian n Skew-symmetric matrix: n Skew-Hermitian matrix:

Skew-symmetric matrices Form n Let A be a skew-symmetric matrix, then A is the following form r

Skew-Hermitian matrices

Skew-Hermitian matrices Form n Let H be a skew-Hermitian matrix, then H is the following form

Symmetric and Hermitian matrices n If A is a real matrix, then n For real matrice, Hermitian matrices and (real) symmetric matrices are the same.

Symmetric and Hermitian matrices n Since every real Hermitian matrix is real symmetric, almost every result for Hermitian matrices has a corresponding result for real symmetric matrices.

Given Example for almost n p. 1 A result for Hermitian matrice: If A is a Hermitian matrix, then there is a unitary matrix U such that n We must by a parallel proof obtain the following result for real symmetric matrices

Given Example for almost n p. 2 A result for real symmetric matrice: If A is a real symmetric matrix, then there is a real orthogonal matrix P such that

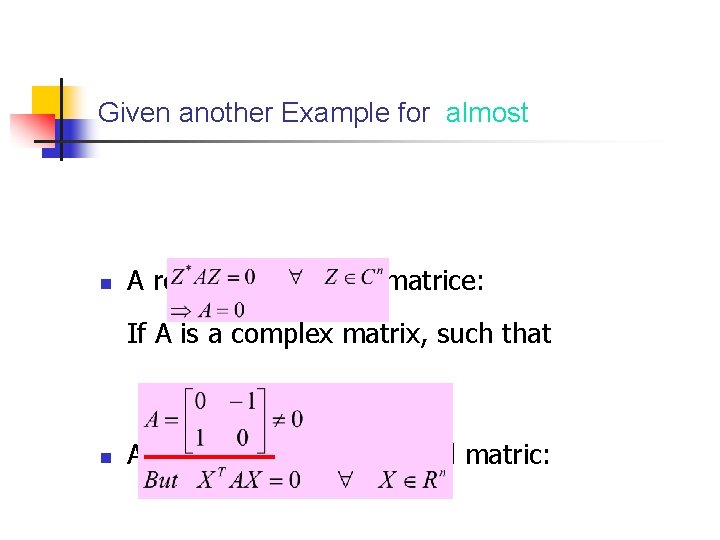
Given another Example for almost n A result for complex matrice: If A is a complex matrix, such that n A counterexample for real matric:

Eigenvalue of a Linear Transformation p. 1 n Eigenvalues of a linear transformation on a real vector space are real numbers. This is by definition.

Eigenvalue of a Linear Transformation p. 2 n We can extend T as following: n Similarly, we can extend A as following

Fact: 1. 1. 1 p. 1

Fact: 1. 1. 1 p. 2

Fact: 1. 1. 1 p. 3

Fact: 1. 1. 1 n p. 4 Corresponding real version also hold.

Fact: 1. 1. 1 p. 5 n If , in addition , m=n, then n Corresponding real version also hold.

Fact: 1. 1. 2 n p. 1 If A is Hermitian, then is Hermitian for k=1, 2, …, n n If A is Hermitian and A is nonsingular, then is Hermitian.

Fact: 1. 1. 2 n p. 1 Therefore, AB is Hermitian if and only if AB=BA

Theorem 1. 1. 4 n A square matrix A is a product of two Hermitian matrices if and only if A is similar to

Proof of Theorem 1. 1. 4 n p. 1 Necessity: Let A=BC, where B and C are Hermitian matrices Then and inductively for any positive integer k (*)

Proof of Theorem 1. 1. 4 n p. 2 We may write, without loss of generality visa similarity where J and K contain Jordan blocks of eigenvalues 0 and nonzero, respectively. Note that J is nilpotent and K is invertible.

Proof of Theorem 1. 1. 4 n p. 3 Partition B and C conformally with A as Then (*) implies that for any positive integer

Proof of Theorem 1. 1. 4 p. 4 Notice that It follows that M=0, since K is nonsingular Then A=BC is the same as

Proof of Theorem 1. 1. 4 p. 5 This yields K=NR, and hence N and R are nonsigular. Taking k=1 in (*), we have

Proof of Theorem 1. 1. 4 p. 6 which gives or, since N is invertible, In other words, K is similar to Since J is similar to , It follows that A is similar to

Proof of Theorem 1. 1. 4 n p. 7 Sufficiency: Notice that This says that if A is similar to a product of two Hermitian matrices, then A is in fact a product of two Hermitian matrice

Proof of Theorem 1. 1. 4 n p. 8 Theorem 3. 13 says that if A is similar to that , then the Jorden blocks of nonreal eigenvalues of A occur in cojugate pairs. Thus it is sufficient to show that

Proof of Theorem 1. 1. 4 n p. 9 Where J(λ) is the Jorden block with λ on the diagonal, is similar to a product of two Hermitian matrices. This is seen as follows:

Proof of Theorem 1. 1. 4 p. 10 which is equal to a product of two Hermitian matrices

=the set of all nxn Hermitian matrices =the set of all nxn skew Hermitian matrix. This means that every skew Hermitian matrix can be written in the form i. A where A is Hermitian and conversely.

n Given a skew Hermitian matrix B, B=i(-i. B) where -i. B is a Hermitian matrix.

n ( also ) form a real vector space under matrix addition and multiplication by real scalar with dimension.

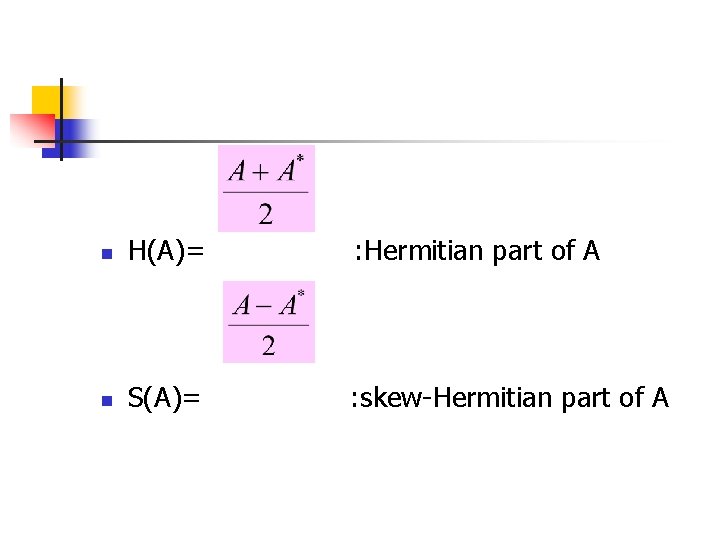
n H(A)= : Hermitian part of A n S(A)= : skew-Hermitian part of A

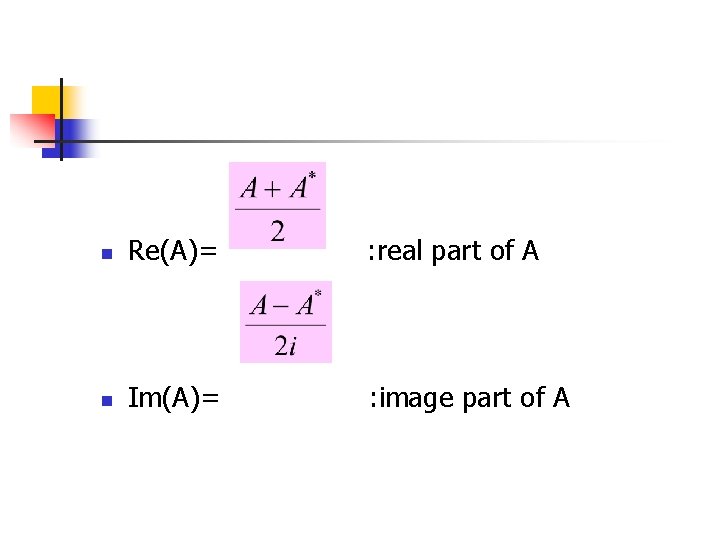
n Re(A)= : real part of A n Im(A)= : image part of A