Chapter One Introduction Single Line Diagram Per Unit

Chapter One : Introduction, Single Line Diagram, Per Unit System and Network Matrices. Prepared by: Ismael K. Saeed 1

INTRODUCTION Modern Power Systems v Power Producer q generation station • prime mover and generator • step-up transformer v Transmission System q HV transmission lines q switching stations • circuit breakers • transformers v Distribution Utility q distribution substations • step-down transformers q MV distribution feeders • distribution transformers Prepared by: Ismael K. Saeed 2

System Control v Network Protection v Energy Management Systems Energy Control Centre • computer control • SCADA - Supervisory Control And Data Acquisition Prepared by: Ismael K. Saeed 3

q Practical power systems • must be safe • reliable • economical q System Analysis • for system planning • for system operations • requires component modelling • types of analysis Ø transmission line performance Ø power flow analysis Ø economic generation scheduling Ø fault and stability studies Prepared by: Ismael K. Saeed 4

System Modelling v Systems are represented on a per-phase basis q A single-phase representation is used for a balanced system • The system is modelled as one phase of a Y-connected network q. Symmetrical components are used for unbalanced systems • Unbalance systems may be caused by: generation, network components, loads, or unusual operating conditions such as faults • The per-unit system of measurements is used Prepared by: Ismael K. Saeed 5

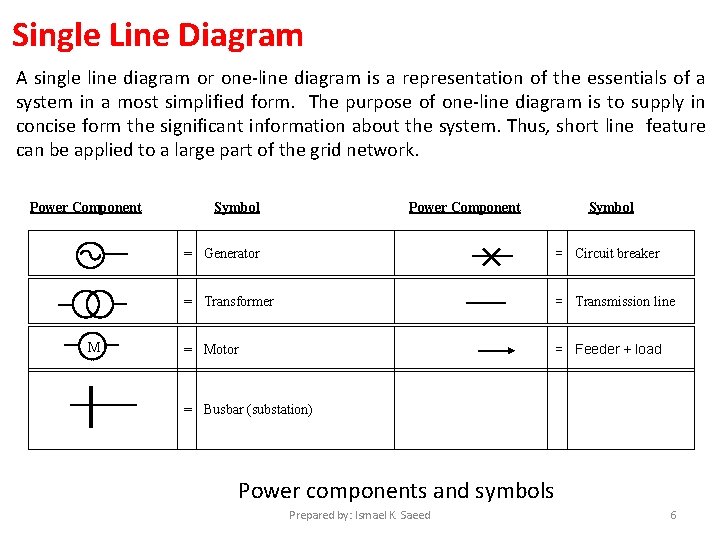
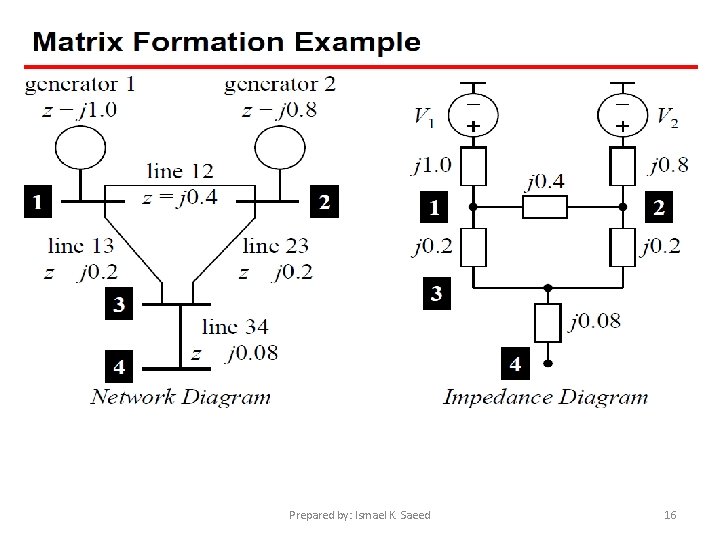
Single Line Diagram A single line diagram or one-line diagram is a representation of the essentials of a system in a most simplified form. The purpose of one-line diagram is to supply in concise form the significant information about the system. Thus, short line feature can be applied to a large part of the grid network. Power Component M Symbol Power Component Symbol = Generator = Circuit breaker = Transformer = Transmission line = Motor = Feeder + load = Busbar (substation) Power components and symbols Prepared by: Ismael K. Saeed 6

Per-Unit Quantities Prepared by: Ismael K. Saeed 7

Prepared by: Ismael K. Saeed 8

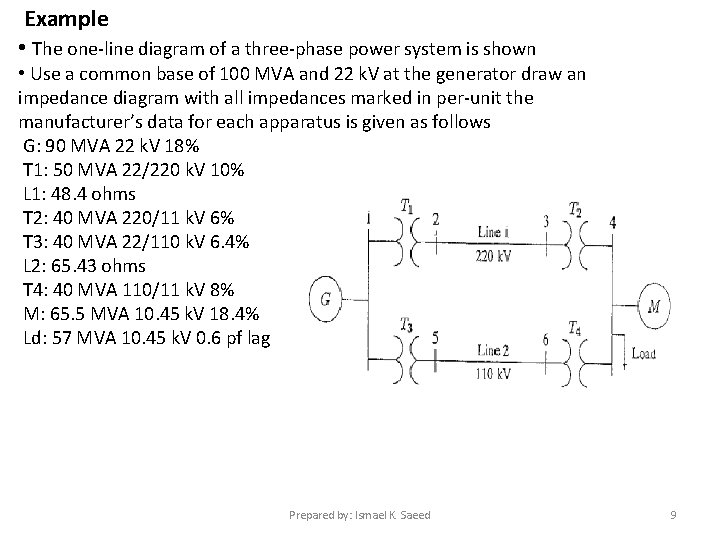
Example • The one-line diagram of a three-phase power system is shown • Use a common base of 100 MVA and 22 k. V at the generator draw an impedance diagram with all impedances marked in per-unit the manufacturer’s data for each apparatus is given as follows G: 90 MVA 22 k. V 18% T 1: 50 MVA 22/220 k. V 10% L 1: 48. 4 ohms T 2: 40 MVA 220/11 k. V 6% T 3: 40 MVA 22/110 k. V 6. 4% L 2: 65. 43 ohms T 4: 40 MVA 110/11 k. V 8% M: 65. 5 MVA 10. 45 k. V 18. 4% Ld: 57 MVA 10. 45 k. V 0. 6 pf lag Prepared by: Ismael K. Saeed 9

Since generator and Transformer voltage bases are the same as their rated values, their per-unit reactances on a 100 MVA base are: Prepared by: Ismael K. Saeed 10

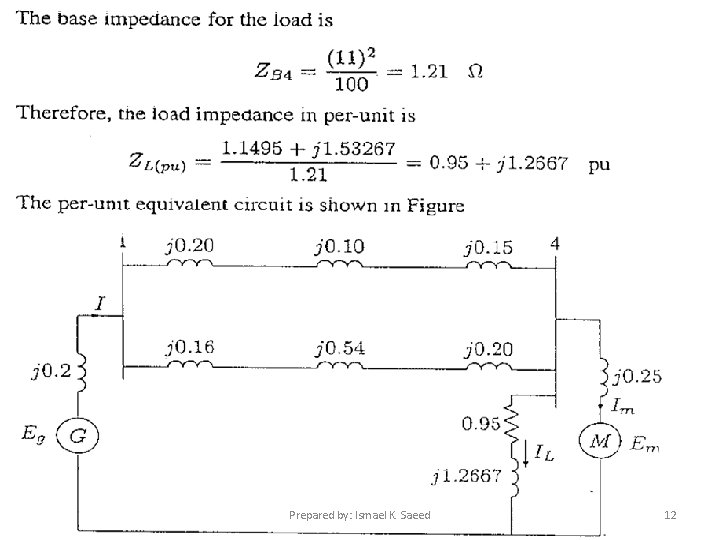
Motor reactance on a 100 MVA, 11 k. V base is Impedance bases for lines 1 and 2 are: Lines 1 and 2 per-unit reactances are: The load apparent power at 0. 6 power factor lagging is given by Hence, the load impedance in ohms is Prepared by: Ismael K. Saeed 11

Prepared by: Ismael K. Saeed 12

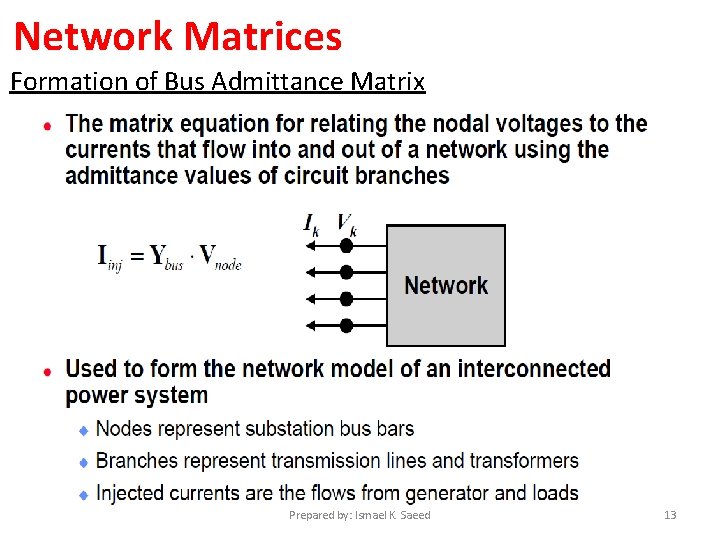
Network Matrices Formation of Bus Admittance Matrix Prepared by: Ismael K. Saeed 13

Consider node (bus) 1 that is connected to the nodes 2 and 3. Then applying KCL at this node we get In a similar way application of KCL at nodes 2, 3 and 4 results in the following equations Prepared by: Ismael K. Saeed 14

Prepared by: Ismael K. Saeed 15

Prepared by: Ismael K. Saeed 16

Prepared by: Ismael K. Saeed 17

Prepared by: Ismael K. Saeed 18

Node Elimination by Kron Reduction Consider an equation of the form where A is an ( n X n ) real or complex valued matrix, x and b are vectors in either Rn or Cn. assume that the b vector has a zero element in the n th row is given as We can then eliminate the kth row and kth column to obtain a reduced ( n - 1) number of equations of the form Prepared by: Ismael K. Saeed 19

Prepared by: Ismael K. Saeed 20

Example: The nodal admittance equations of the system in p. u values is using Y 22 as the initial pivot, eliminate node 2 and the corresponding voltage v 2 from 4 * 4 system. Solution: Prepared by: Ismael K. Saeed 21

Similar calculations yields the other elements of the KRON-reduced matrix (1) (3) (4) Prepared by: Ismael K. Saeed 22