Chapter IV Ship HydroStatics Dynamics Floatation Stability 4

Chapter IV (Ship Hydro-Statics & Dynamics) Floatation & Stability

4. 1 Important Hydro-Static Curves or Relations (see Fig. 4. 11 at p 44 & handout) • Displacement Curves (displacement [molded, total] vs. draft, weight [SW, FW] vs. draft (T)) • Coefficients Curves (CB , CM , CP , CWL, vs. T) • VCB (KB, ZB): Vertical distance of Center of Buoyancy (C. B) to the baseline vs. T • LCB (LCF, XB): Longitudinal Distance of C. B or floatation center (C. F) to the midship vs. T

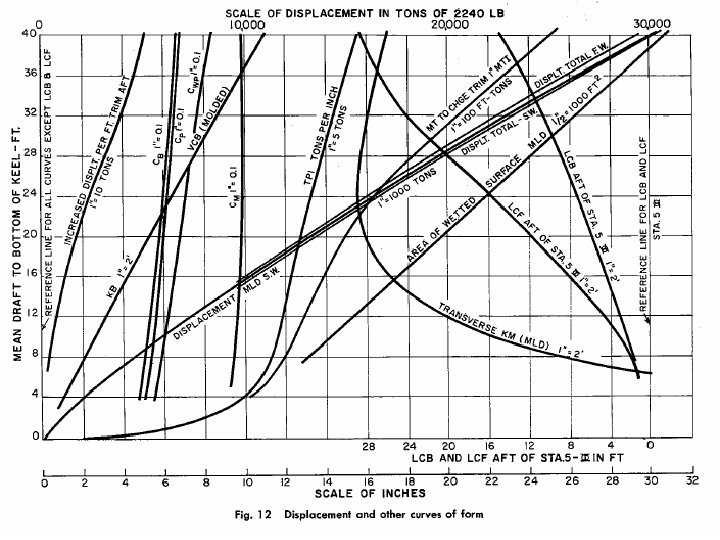
4. 1 Important Hydro-Static Curves or Relations (Continue) • TPI: Tons per inch vs. T (increase in buoyancy due to per inch increase in draft) • Bonbjean Curves (p 63 -66) a) Outline profile of a hull b) Curves of areas of transverse sections (stations) c) Drafts scales d) Purpose: compute disp. & C. B. , when the vessel has 1) a large trim, or 2)is poised on a big wave crest or trough.

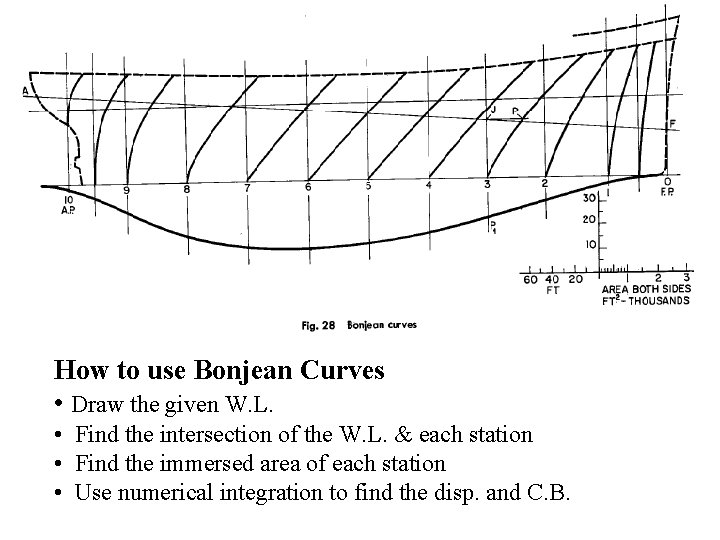
How to use Bonjean Curves • Draw the given W. L. • Find the intersection of the W. L. & each station • Find the immersed area of each station • Use numerical integration to find the disp. and C. B.

4. 2 How to Compute these curves • Formulas for Area, Moments & Moments of Inertia

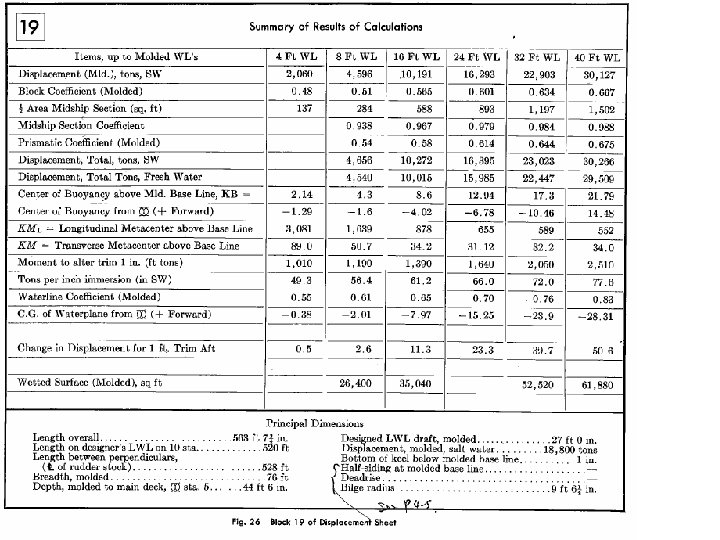
Examples of Hand Computation of Displacement Sheet (Foundation for Numerical Programming) • Area, floatation, etc of 24’ WL (Waterplane) • Displacement (molded) up to 8’ WL • Displacement (molded) up to 24’ and 40 ‘WL (vertical summation of waterplanes) • Displacement (molded) up to 24’ and 40 ‘WL (Longitudinal summation of stations) • Wetted surface • Summary of results of Calculations

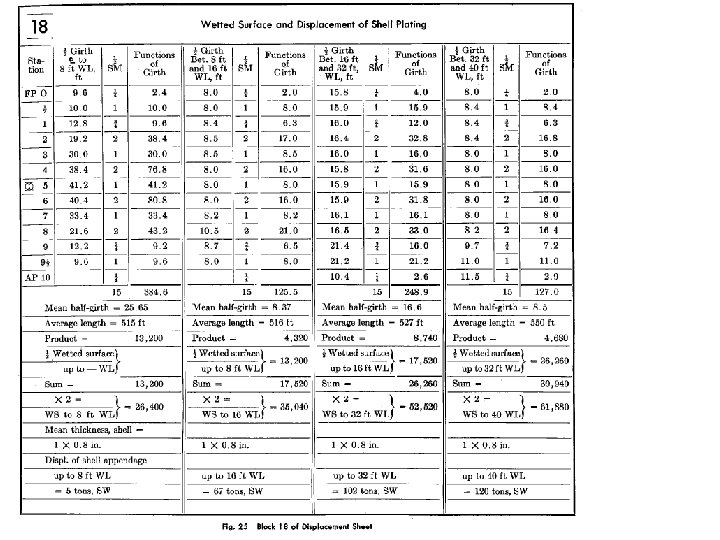
4’wl area 32’wl area 8’wl area 40’wl area 16’wl area Up to 4’wl 24’wl area Up to 8’wl MTI Disp. Up to 16’wl Disp. Up to 32’wl • 12 -15 Transverse station area, longitudinal integration for displacement, ZB , and XB MTI Wetted surface Disp. Up to 40’wl • 1 -6 Areas & properties (F. C. , Ic, etc) of W. L • 7 -11 Displacement, ZB , and XB up W. L. , vertical integration. Up to 24’ & 40 wl Disp. Up to 24’wl Red sheet will be studied in detail Summary • 16 -18 Specific Feature (wetted surface, MTI, etc. • 19 Summary

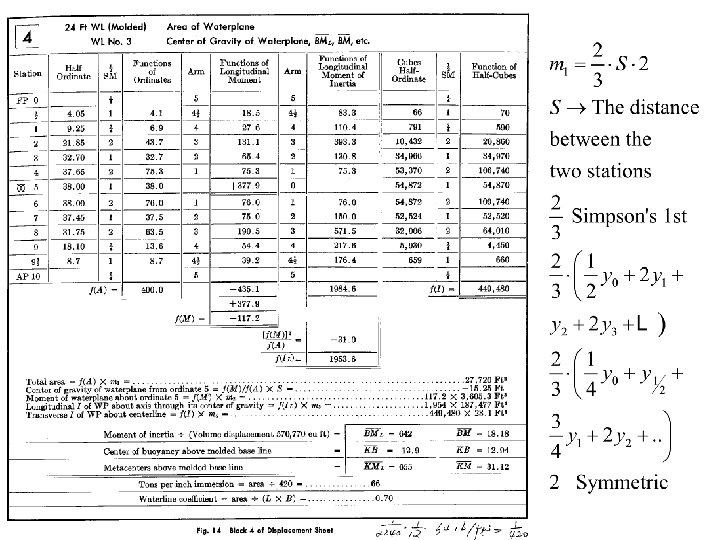
Illustration of Table 4: C 1 Station FP-0 C 2 Half Ordinate copy from line drawing table ( 24’ WL). (notice at FP. Modification of half ordinate) C 3 Simpson coefficient (Simpson rule 1) (1/2 because of half station) C 4 = C 3 x C 2 AP-10 (half station) (area function) displacement C 5 = Arm (The distance between a station and station of 5 (Midship) C 6 = C 5 x Function of Longitudinal Moment with respect to Midship (or station 5) C 7 = Arm (same as C 5) C 8 = C 6 x C 7 Function of Longitudinal moment of inertia with respect to Midship. C 9. = [C 2]3 C 10. Same as C 3. C 11. = C 9 x C 10. (Simpson Coeff. ) Transverse moment of inertia of WL about its centerline Table 5 is similar to Table 4, except the additional computation of appendage.

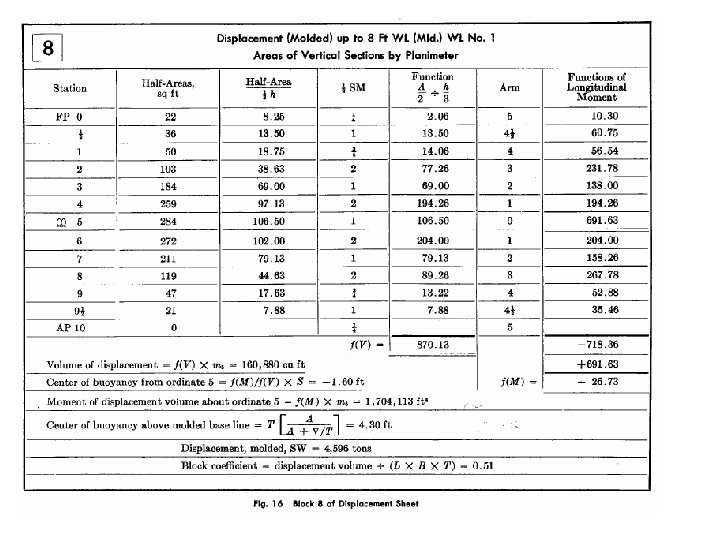
Illustration of Table 8 For low WLs, their change is large. Therefore, it is first to use planimeter or other means to compute the half-areas of each stations up to No. 1 WL (8’ WL). C 1. Station C 2. Half area (ft 2) of the given station C 3/(h/3) ( divided by h/3 is not meaningful, because it later multiplying by h/3) (h = 8’ the distance between the two neighboring WLs) C 4. ½ Simpson’s Coeff. C 5. C 4 x C 3 C 6. Arm distance between this station and station 5 (midship) C 7 C 5 x C 6 f(M)

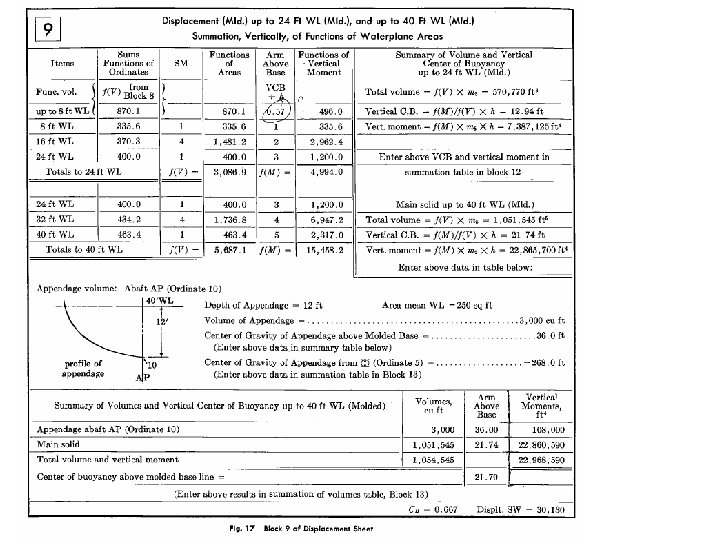
Illustration of Table 9 C 1. WL No. C 2. f(V) Notice first row up to 8’. f(v) C 3. Simpson’s coeff. C 4. C 2 x C 3 C 5. Vertical Arm above the base C 6. C 4 x C 5. f(m) vertical moment w. r. t. the Baseline. * Notice up the data in the first row is related to displacement up to 8’ WL. The Table just adding V)

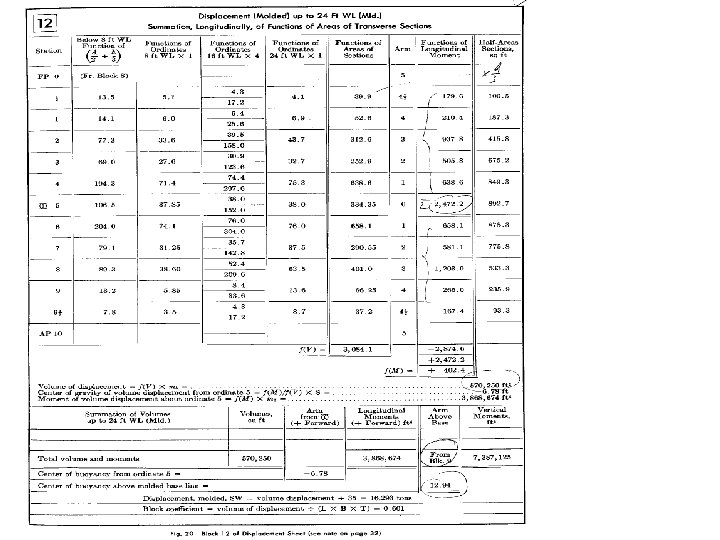
Illustration of Table 12 C 1. Station No. C 2. under 8’ WL. (From Table 8) C 3. 8’ WL x 1 C 4. 16’ WL x¼ C 5. 24’ WL x 1 C 6. (C 2 + C 3 + C 4 + C 5) Function of Area of Stations C 7. Arm C 8. C 7 x C 6 (Simpson rule) C 9. C 6*h/3 (SM 1 + 4 + 1) (Distance between this station to midship)

4. 3 Stability A floating body reaches to an equilibrium state, if 1) its weight = the buoyancy 2) the line of action of these two forces become collinear. The equilibrium: stable, or unstable or neutrally stable. • Stable equilibrium: if it is slightly displaced from its equilibrium position and will return to that position. • Unstable equilibrium: if it is slightly displaced form its equilibrium position and tends to move farther away from this position. • Neutral equilibrium: if it is displaced slightly from this position and will remain in the new position.

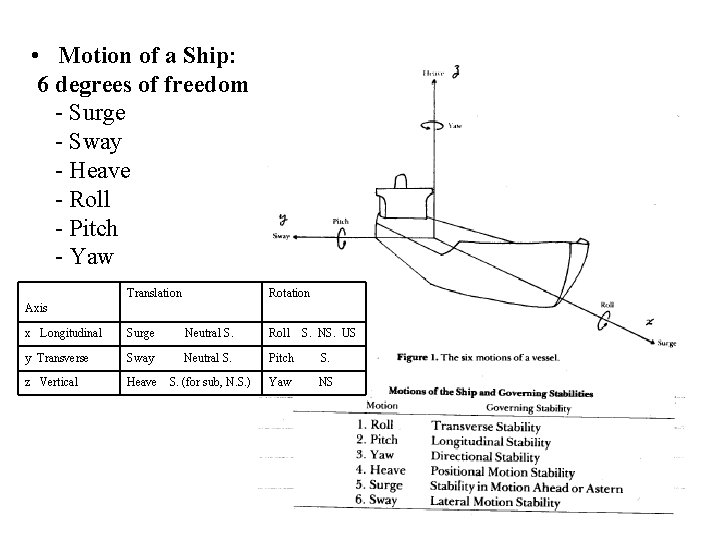
• Motion of a Ship: 6 degrees of freedom - Surge - Sway - Heave - Roll - Pitch - Yaw Translation Rotation Axis x Longitudinal Surge Neutral S. Roll S. NS. US y Transverse Sway Neutral S. Pitch S. z Vertical Heave S. (for sub, N. S. ) Yaw NS

Righting & Heeling Moments A ship or a submarine is designed to float in the upright position. • Righting Moment: exists at any angle of inclination where the forces of weight and buoyancy act to move the ship toward the upright position. • Heeling Moment: exists at any angle of inclination where the forces of weight and buoyancy act to move the ship away from the upright position.

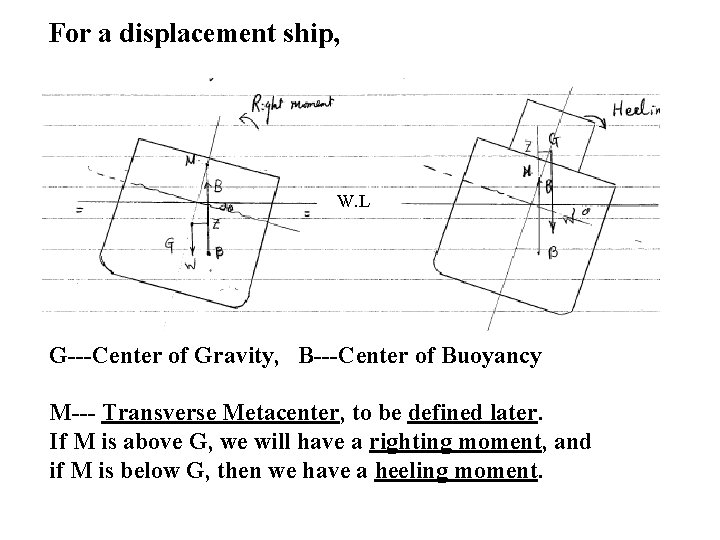
For a displacement ship, W. L G---Center of Gravity, B---Center of Buoyancy M--- Transverse Metacenter, to be defined later. If M is above G, we will have a righting moment, and if M is below G, then we have a heeling moment.

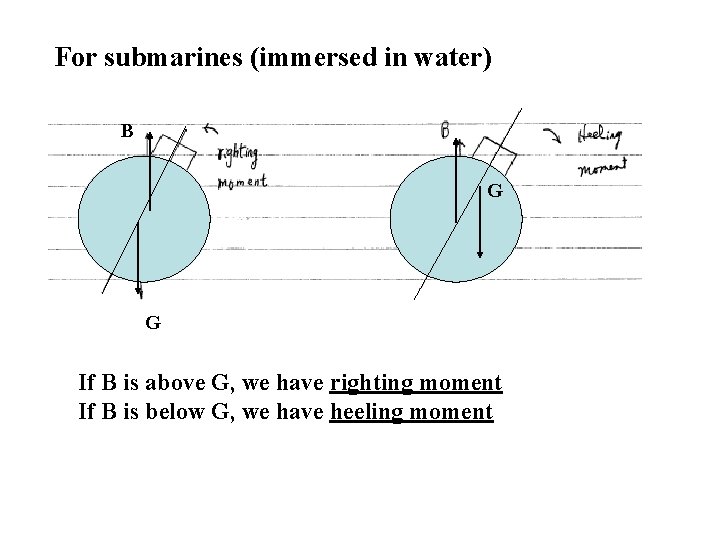
For submarines (immersed in water) B G G If B is above G, we have righting moment If B is below G, we have heeling moment

Upsetting Forces (overturning moments) • Beam wind, wave & current pressure • Lifting a weight (when the ship is loading or unloading in the harbor. ) • Offside weight (C. G is no longer at the center line) • The loss of part of buoyancy due to damage (partially flooded, C. B. is no longer at the center line) • Turning • Grounding

Longitudinal Equilibrium For an undamaged (intact) ship, we are usually only interested in determining the ship’s draft and trim regarding the longitudinal equilibrium because the ship capsizing in the longitudinal direction is almost impossible. We only study the initial stability for the longitudinal equilibrium.

Static Stability & Dynamical Stability Static Stability: Studying the magnitude of the righting moment given the inclination (angle) of the ship*. Dynamic Stability: Calculating the amount of work done by the righting moment given the inclination of the ship. The study of dynamic Stability is based on the study of static stability.

• Static Stability 1) The initial stability (aka stability at small inclination) and, 2) the stability at large inclinations. • The initial (or small angle) stability: studies the right moments or right arm at small inclination angles. • The stability at large inclination (angle): computes the right moments (or right arms) as function of the inclination angle, up to a limit angle at which the ship may lose its stability (capsizes). Hence, the initial stability can be viewed as a special case of the latter.

Initial stability • Righting Arm: A symmetric ship is inclined at a small angle dΦ. C. B has moved off the ship’s centerline as the result of the inclination. The distance between the action of buoyancy and weight, GZ, is called righting arm. • Transverse Metacenter: A vertical line through the C. B intersects the original vertical centerline at point, M.

Location of the Transverse Metacenter Transverse metacentric height : the distance between the C. G. and M (GM). It is important as an index of transverse stability at small angles of inclination. GZ is positive, if the moment is righting moment. M should be above C. G, if GZ >0. If we know the location of M, we may find GM, and thus the righting arm GZ or righting moment can be determined given a small angle dΦ. How to determine the location of M?

When a ship is inclined at small angle dΦ Wo. Lo – Waterline (W. L) at upright position W 1 L 1 – Inclined W. L Bo – C. B. at upright position, B 1 – C. B. at inclined position - The displacement (volume) of the ship v 1, v 2 – The volume of the emerged and immersed g 1, g 2 – C. G. of the emerged and immersed wedge, respectively

Equivolume Inclination (v 1 =v 2 ) If the ship is wall-sided with the range of inclinations of a small angle dΦ, then the volume v 1 and v 2 , of the two wedges between the two waterlines will be same. Thus, the displacements under the waterlines Wo. Lo and W 1 L 1 will be same. This inclination is called equivolume inclination. Thus, the intersection of Wo. Lo, and W 1 L 1 is at the longitudinal midsection. For most ships, while they may be wall-sided in the vicinity of WL near their midship section, they are not wall-sided near their sterns and bows. However, at a small angle of inclination, we may still approximately treat them as equivolume inclination.

When a ship is at equivolume inclination, According to a theorem from mechanics, if one of the bodies constituting a system moves in a direction, the C. G. of the whole system moves in the same direction parallel to the shift of the C. G. of that body. The shift of the C. G. of the system and the shift of the C. G of the shifted body are in the inverse ratio of their weights.

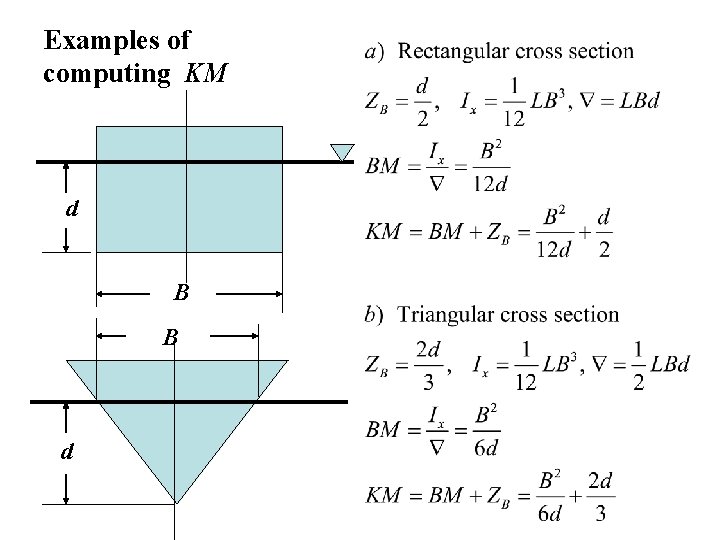
Examples of computing KM d B B d

Natural frequency of Rolling of A Ship

4. 4 Effects of free surfaces of liquids on the righting arm pp 81 -83 • When a liquid tank in a ship is not full, there is a free surface in this tank. • The effect of the free surface of liquids on the initial stability of the ship is to decrease the righting arm. For a small parallel angle inclination, the movement of C. G of liquid is

• The increase in the heeling moment due to the movement of C. G. of liquid If there is no influence of free-surface liquids, the righting moment of the ship at a small angle dΦ is: In the presence of a free-surface liquid, the righting moment is decreased due to a heeling moment of free-surface liquid. The reduced righting moment M’ is

The reduced metacentric height GM’: Comparing with the original GM, it is decreased by an amount, The decrease can also be viewed as an increase in height of C. G. w. r. t. the baseline. How to decrease IOL: • Longitudinal subdivision: reduce the width b, and thus reduces Anti rolling tank

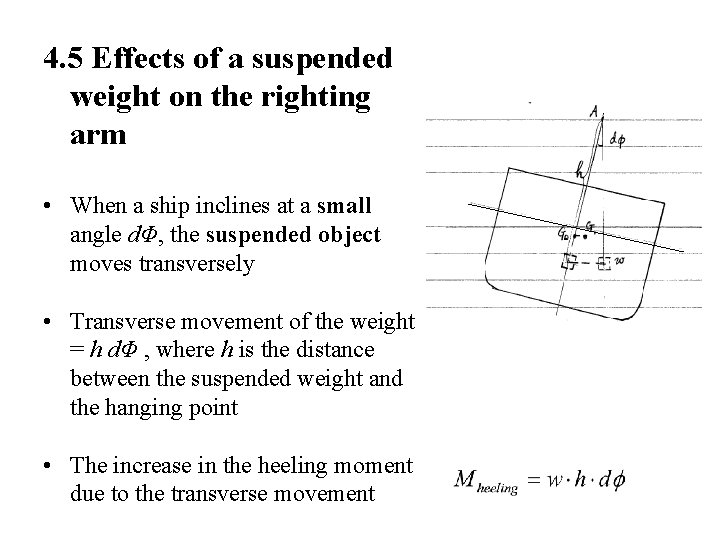
4. 5 Effects of a suspended weight on the righting arm • When a ship inclines at a small angle dΦ, the suspended object moves transversely • Transverse movement of the weight = h dΦ , where h is the distance between the suspended weight and the hanging point • The increase in the heeling moment due to the transverse movement

In the presence of a suspended object, the righting moment & righting arm are decreased due to a heeling moment of the suspended object. The reduced righting moment M’ & metacentric height GM’ are: In other words, the C. G of a suspended object is actually at its suspended point

Because the suspension weights & liquid with free surface tend to decrease the righting arm, or decrease the initial stability, we should avoid them. 1. Filling the liquid tank (in full) to get rid of the free surface. (creating a expandable volume) 2. Make the inertial moment of the free surface as small as possible by adding the separation longitudinal plates (bulkhead). 3. Fasten the weights to prevent them from moving transversely.

4. 6 The Inclining Experiment (Test) Purpose 1. To obtain the vertical position of C. G (Center of Gravity) of the ship. 2. It is required by “International convention on Safety of Life at Sea. ” (Every passenger or cargo vessel newly built or rebuilt)

4. 6 The Inclining Experiment (Continue) Basic Principle M: Transverse Metacenter (A vertical line through the C. B intersects the original vertical centerline at point, M) Due to the movement of weights, the heeling moment is where w is the total weight of the moving objects and h is the moving distance.

4. 6 The Inclining Experiment (Continue) The shift of the center of gravity is where W is the total weight of the ship. The righting moment = The heeling moment 1. w and h are recorded and hence known. 2. is measured by a pendulum known as stabilograph. 3. The total weight W can be determined given the draft T. (at FP, AP & midship, usually only a very small trim is allowed. ) 4. Thus GM can be calculated,

4. 6 The Inclining Experiment (Continue) The metacenter height and vertical coordinate of C. B have been calculated. Thus, C. G. can be obtained. Obtaining the longitudinal position of the gravity center of a ship will be explained in section 4. 8.

4. 6 The Inclining Experiment (Continue) 1. The experiment should be carried out in calm water & nice weather. No wind, no heavy rain, no tides. 2. It is essential that the ship be free to incline (mooring ropes should be as slack as possible, but be careful. ) . 3. All weights capable of moving transversely should be locked in position and there should be no loose fluids in tanks. 4. The ship in inclining test should be as near completion as possible. 5. Keep as few people on board as possible. 6. The angle of inclination should be small enough with the range of validity of theory. 7. The ship in experiment should not have a large trim.

4. 7 Effect of Ship’s Geometry on Stability Transverse metacenter height GM = BM – (ZG –ZB)

4. 7 (Continue)

• Conclusion: to increase GM ( Transverse metacenter height) 1. increasing the beam, B 2. decreasing the draft, T 3. lowering C. G (ZG) 4. increasing the freeboard will increase the ZG, but will improve the stability at large inclination angle. 5. Tumble home or flare will have effects on the stability at large inclination angle. 6. Bilge keels, fin stabilizers, gyroscopic stabilizers, antirolling tank also improve the stability (at pp 248 -252).

4. 7 (Continue) Suitable metacenter height • It should be large enough to satisfy the requirement of rules. • Usually under full load condition, GM~0. 04 B. • However, too large GM will result in a very small rolling period. Higher rolling frequency will cause the crew or passenger uncomfortable. This also should be avoided. (see page 37 of this notes)

4. 8 Longitudinal Inclination Longitudinal Metacenter: Similar to the definition of the transverse meta center, when a ship is inclined longitudinally at a small angle, A vertical line through the center of buoyancy intersects the vertical line through (before the ship is inclined) at.

• The Location of the Longitudinal Metacenter For a small angle inclination, volumes of forward wedge immersed in water and backward wedge emerged out of water are:

• Location of the Longitudinal Metacenter Using the same argument used in obtaining transverse metacenter.

• Location of the Longitudinal Metacenter

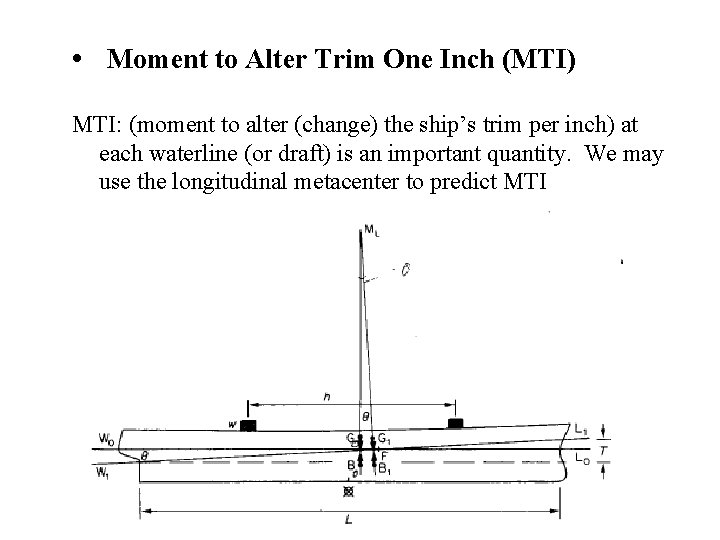
• Moment to Alter Trim One Inch (MTI) MTI: (moment to alter (change) the ship’s trim per inch) at each waterline (or draft) is an important quantity. We may use the longitudinal metacenter to predict MTI

• MTI ( a function of draft) Due to the movement of a weight, assume that the ship as 1” trim, and floats at waterline W. L. ,

• MTI ( a function of draft) • If the longitudinal inclination is small, MTI can be used to find out the longitudinal position of gravity center ( ).