Chapter Four Combinational Logic 1 Discrete quantities of

Chapter Four Combinational Logic 1

Discrete quantities of information are represented in digital systems by binary codes. A binary code of n bits is capable of representing up to 2 n distinct elements of coded information. DECODERS A decoder is a combinational circuit that converts binary information from n input lines to a maximum of 2 n unique output lines. If the n-bit coded information has unused combinations, the decoder may have fewer than 2 n outputs. 2
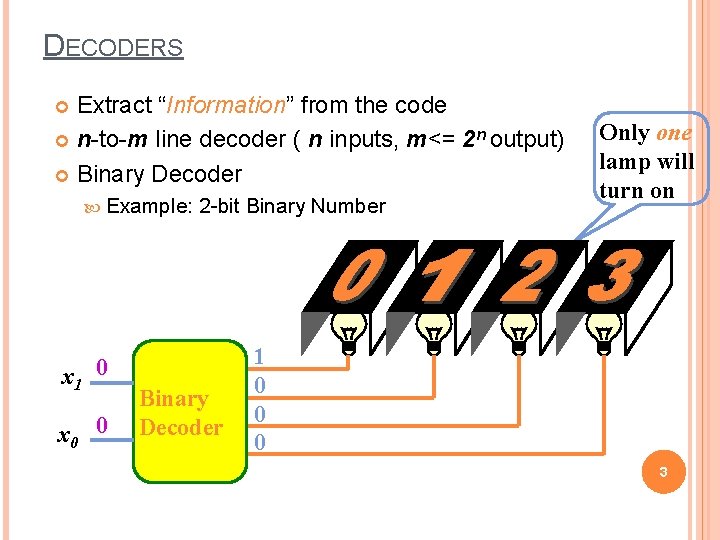
DECODERS Extract “Information” from the code n-to-m line decoder ( n inputs, m<= 2 n output) Binary Decoder Example: x 1 0 x 0 0 2 -bit Binary Number Binary Decoder Only one lamp will turn on 1 0 0 0 3
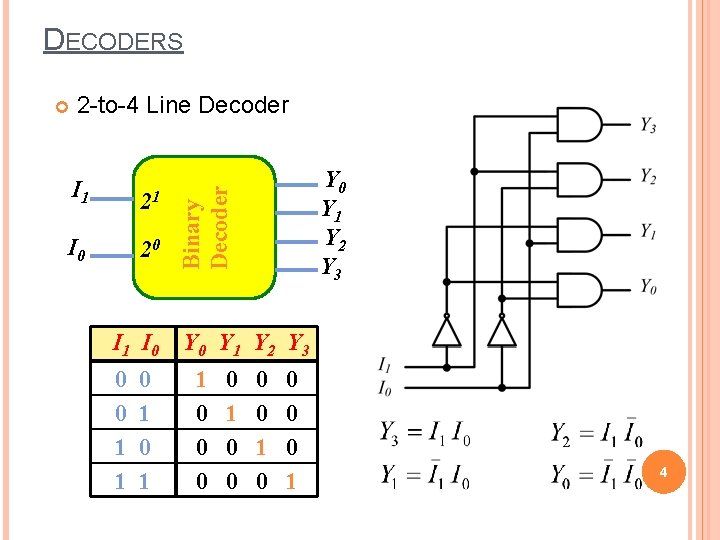
DECODERS 2 -to-4 Line Decoder I 1 21 I 0 20 I 1 I 0 0 0 1 1 0 1 Y 0 Y 1 Y 2 Y 3 Binary Decoder Y 0 Y 1 Y 2 Y 3 1 0 0 0 0 1 4
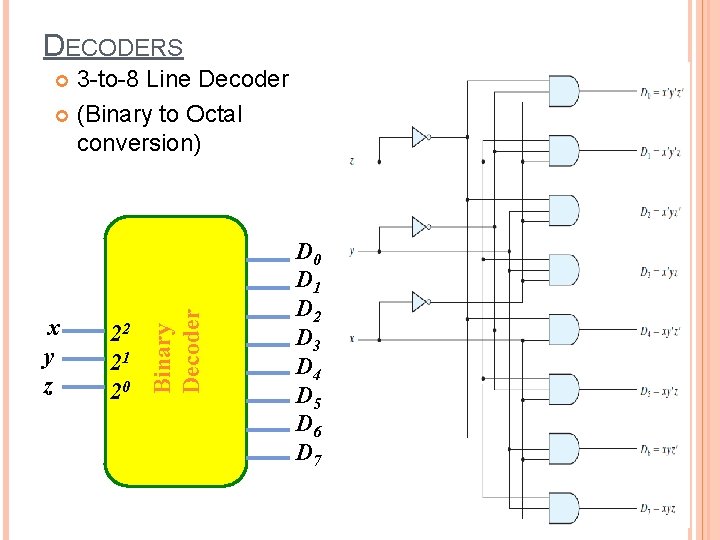
DECODERS 3 -to-8 Line Decoder (Binary to Octal conversion) x y z 22 21 20 Binary Decoder D 0 D 1 D 2 D 3 D 4 D 5 D 6 D 7 5
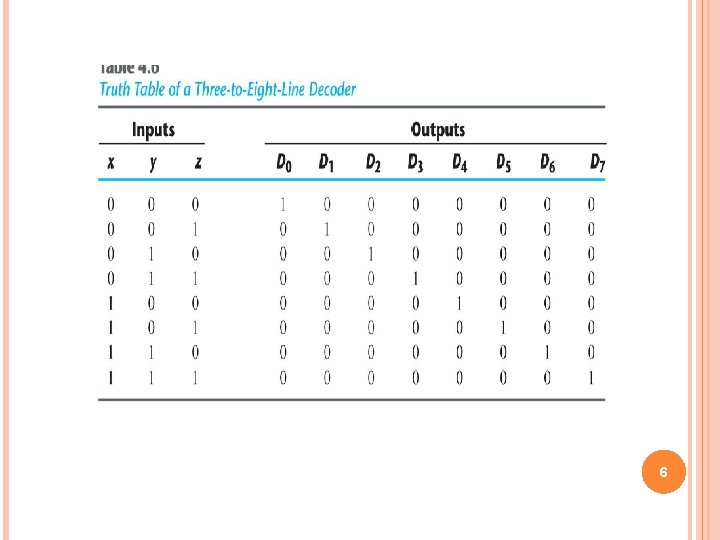
6
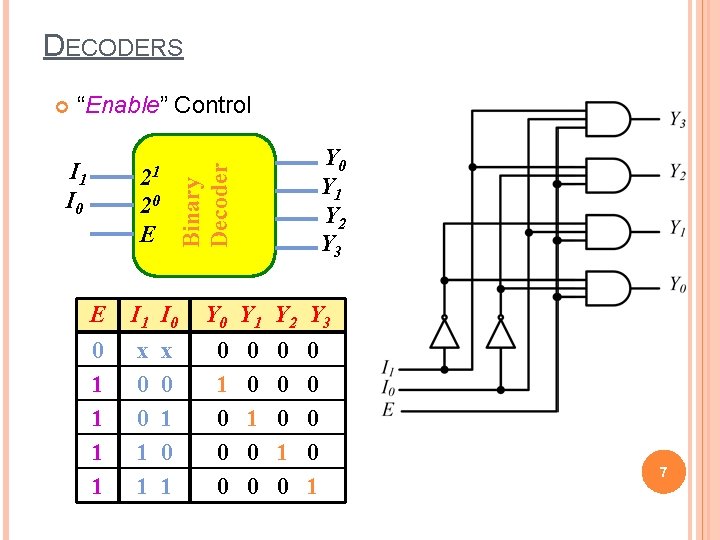
DECODERS “Enable” Control I 1 I 0 Y 1 Y 2 Y 3 Binary Decoder 21 20 E E I 1 I 0 0 1 1 x 0 1 Y 0 Y 1 Y 2 Y 3 0 1 0 0 0 0 0 1 7
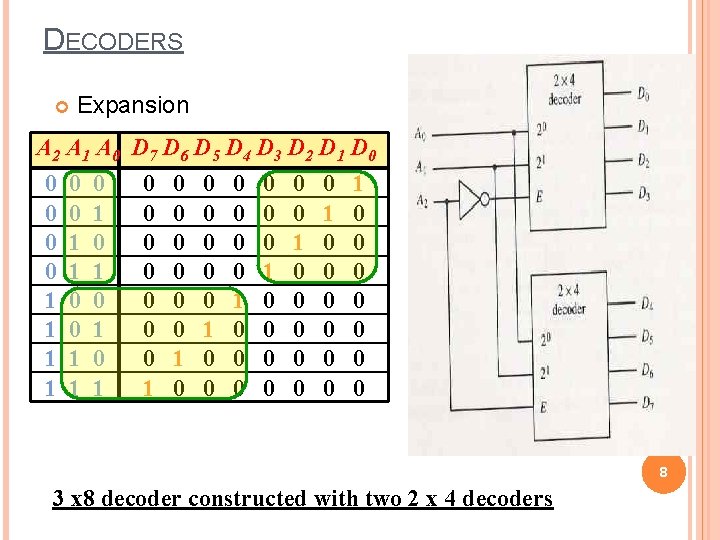
DECODERS Expansion A 2 A 1 A 0 D 7 D 6 D 5 D 4 D 3 D 2 D 1 D 0 0 0 1 1 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 8 3 x 8 decoder constructed with two 2 x 4 decoders
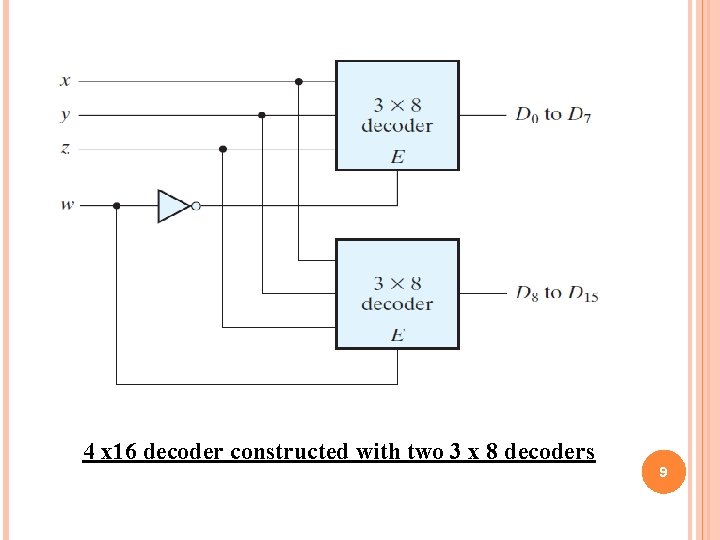
4 x 16 decoder constructed with two 3 x 8 decoders 9
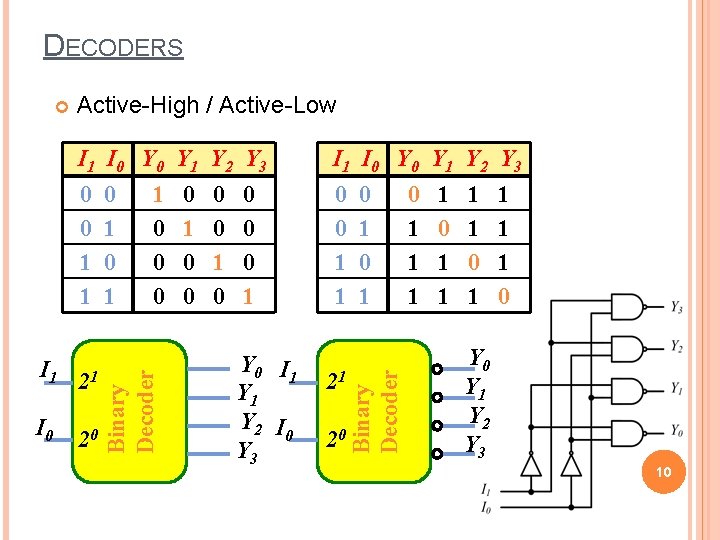
DECODERS Active-High / Active-Low I 1 I 0 Y 0 Y 1 Y 2 Y 3 0 0 1 1 I 0 20 1 0 0 0 0 1 Y 0 I 1 Y 2 I 0 Y 3 21 20 0 1 Binary Decoder I 1 21 0 1 Binary Decoder 0 1 1 1 1 0 Y 1 Y 2 Y 3 10
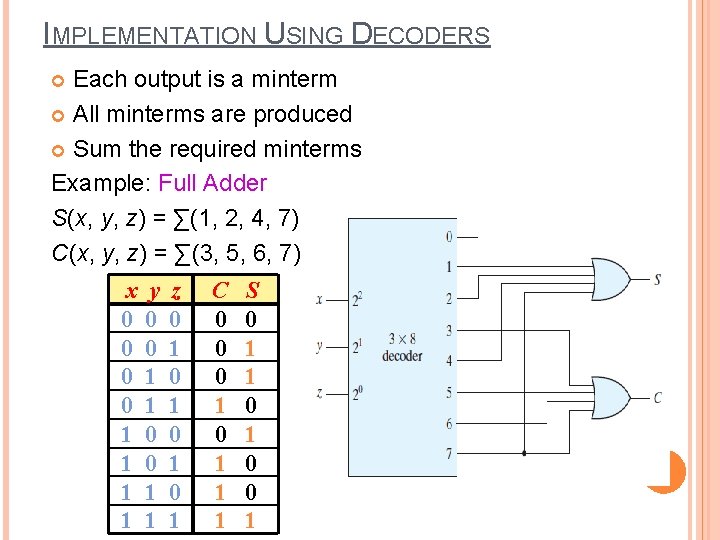
IMPLEMENTATION USING DECODERS Each output is a minterm All minterms are produced Sum the required minterms Example: Full Adder S(x, y, z) = ∑(1, 2, 4, 7) C(x, y, z) = ∑(3, 5, 6, 7) x y 0 0 0 1 0 1 1 1 1 z 0 1 0 1 C 0 0 0 1 1 1 S 0 1 1 0 0 1 11

A function with a long list of minterms requires an OR gate with a large number of inputs. If the number of minterms in the function is greater than 2 n/2, then F’ can be expressed with fewer minterms. So we use a NOR gate to sum the minterms of F’. The output of NOR gate complements this sum and generates the normal output F. 12
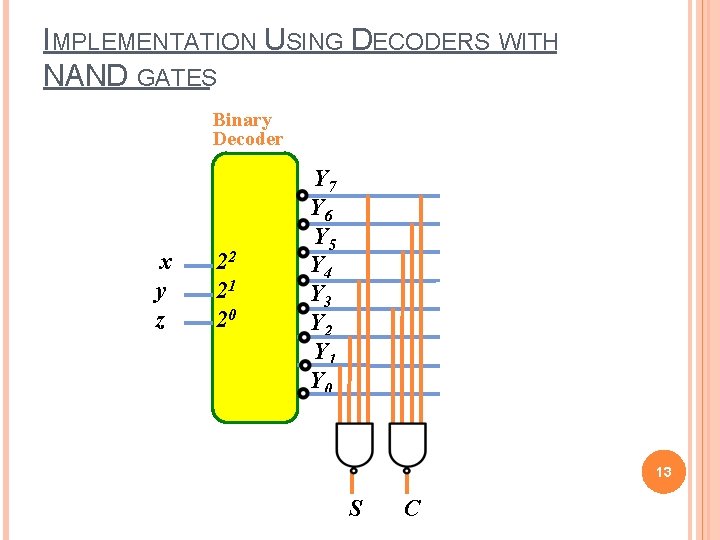
IMPLEMENTATION USING DECODERS WITH NAND GATES Binary Decoder x y z 22 21 20 Y 7 Y 6 Y 5 Y 4 Y 3 Y 2 Y 1 Y 0 13 S C
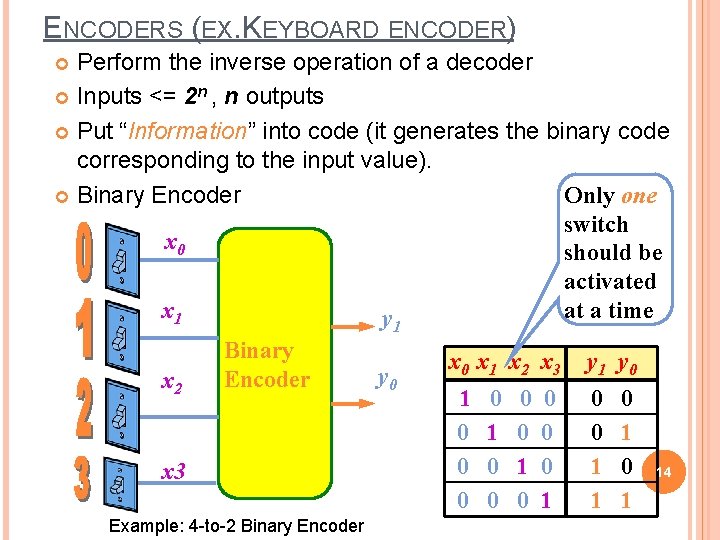
ENCODERS (EX. KEYBOARD ENCODER) Perform the inverse operation of a decoder Inputs <= 2 n , n outputs Put “Information” into code (it generates the binary code corresponding to the input value). Only one Binary Encoder switch x 0 should be activated at a time x 1 y 1 x 2 Binary Encoder x 3 Example: 4 -to-2 Binary Encoder y 0 x 1 x 2 x 3 1 0 0 0 0 1 y 0 0 0 1 14
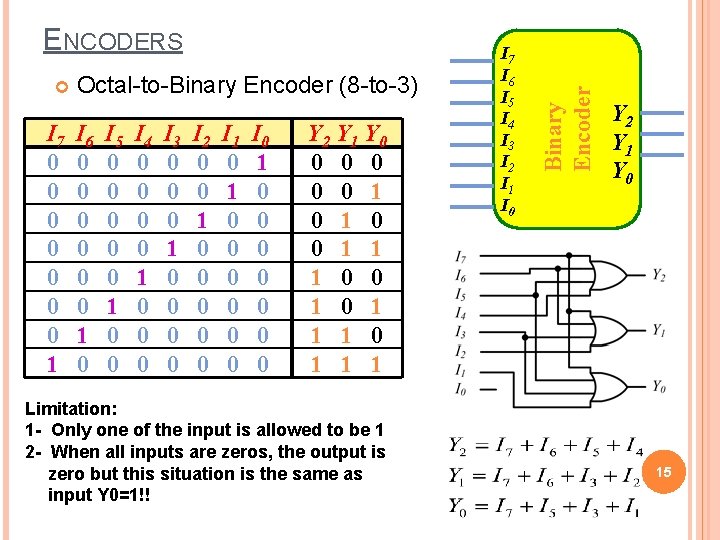
I 7 0 0 0 0 1 Octal-to-Binary Encoder (8 -to-3) I 6 0 0 0 1 0 I 5 0 0 0 1 0 0 I 4 0 0 1 0 0 0 I 3 0 0 0 1 0 0 I 2 0 0 1 0 0 0 I 1 0 0 0 0 I 0 1 0 0 0 0 Y 2 Y 1 Y 0 0 0 1 1 1 0 0 1 1 1 Limitation: 1 - Only one of the input is allowed to be 1 2 - When all inputs are zeros, the output is zero but this situation is the same as input Y 0=1!! I 7 I 6 I 5 I 4 I 3 I 2 I 1 I 0 Binary Encoder ENCODERS Y 2 Y 1 Y 0 15
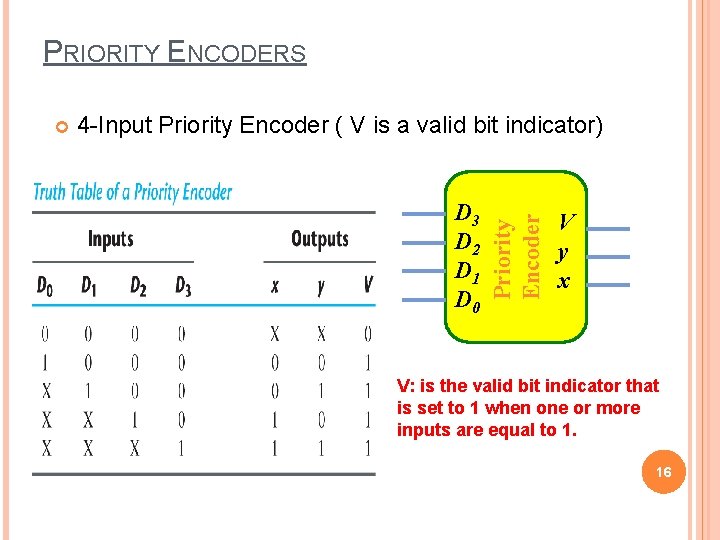
PRIORITY ENCODERS 4 -Input Priority Encoder ( V is a valid bit indicator) D 3 D 2 D 1 D 0 Priority Encoder V y x V: is the valid bit indicator that is set to 1 when one or more inputs are equal to 1. 16
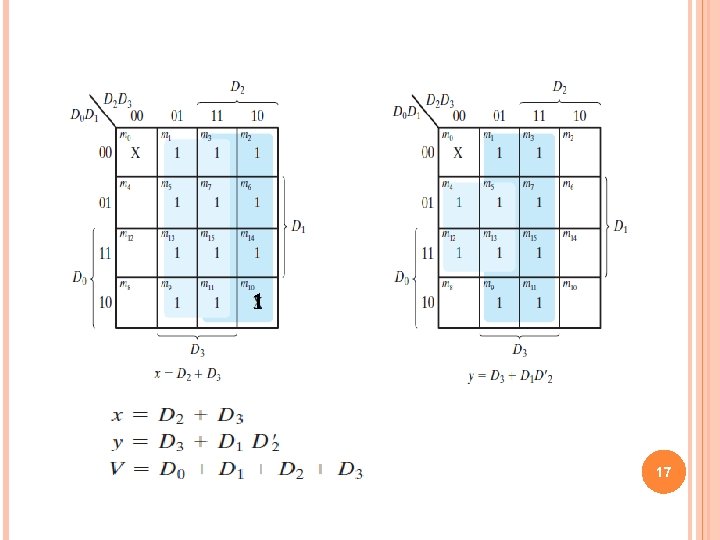
1 17
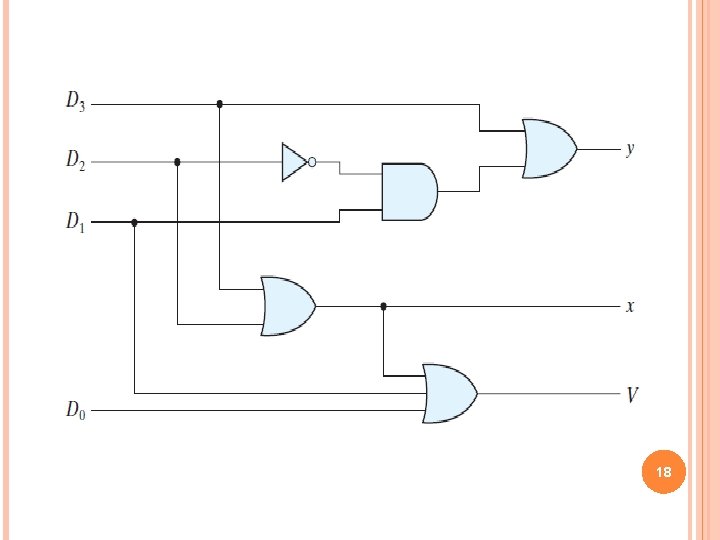
18
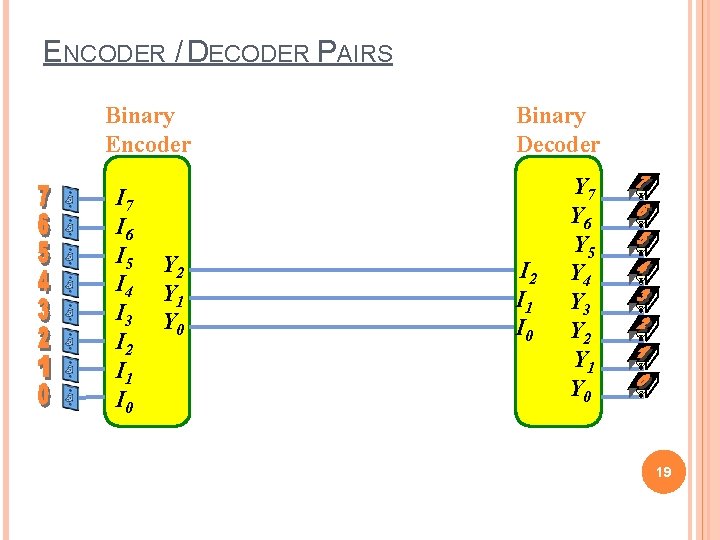
ENCODER / DECODER PAIRS Binary Encoder I 7 I 6 I 5 I 4 I 3 I 2 I 1 I 0 Y 2 Y 1 Y 0 Binary Decoder I 2 I 1 I 0 Y 7 Y 6 Y 5 Y 4 Y 3 Y 2 Y 1 Y 0 19
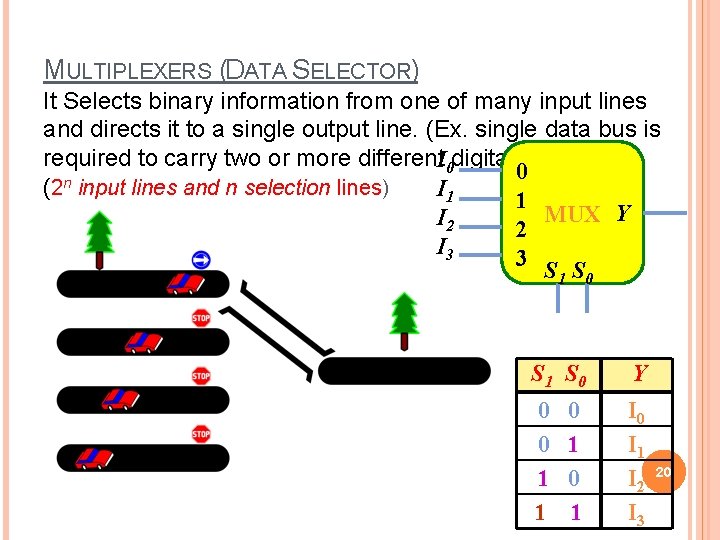
MULTIPLEXERS (DATA SELECTOR) It Selects binary information from one of many input lines and directs it to a single output line. (Ex. single data bus is required to carry two or more different. I 0 digital signals) 0 n (2 input lines and n selection lines) I 1 1 MUX Y I 2 2 I 3 3 S 1 S 0 Y 0 0 1 1 I 0 I 1 I 2 I 3 0 1 20
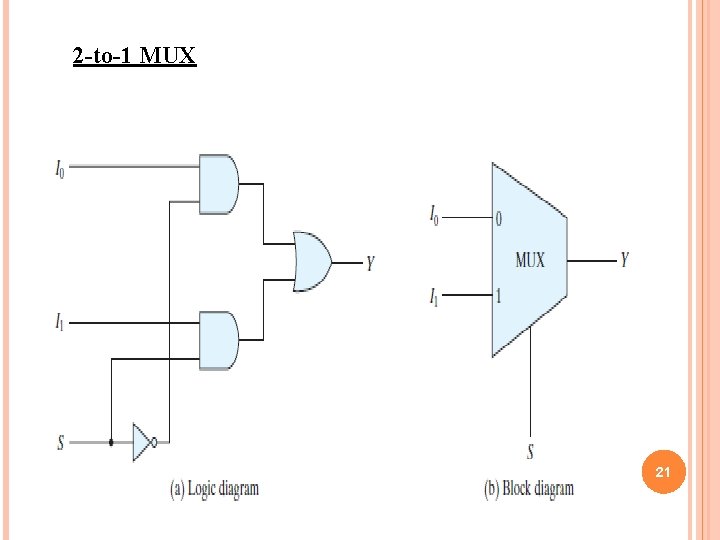
2 -to-1 MUX 21
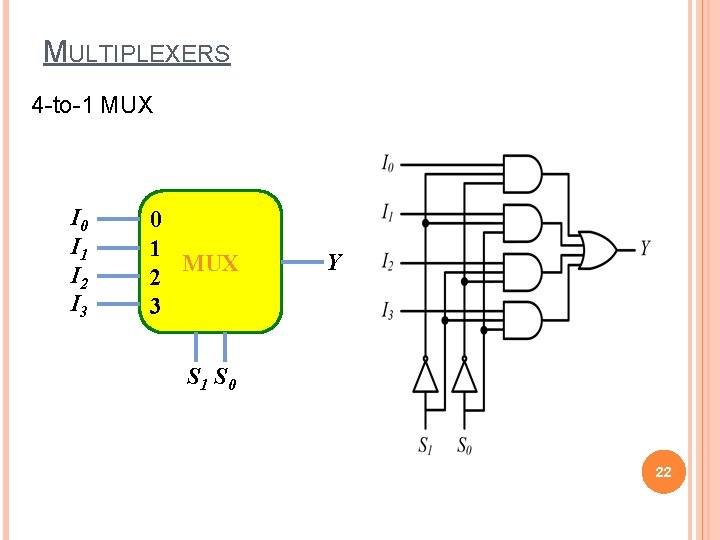
MULTIPLEXERS 4 -to-1 MUX I 0 I 1 I 2 I 3 0 1 MUX 2 3 Y S 1 S 0 22
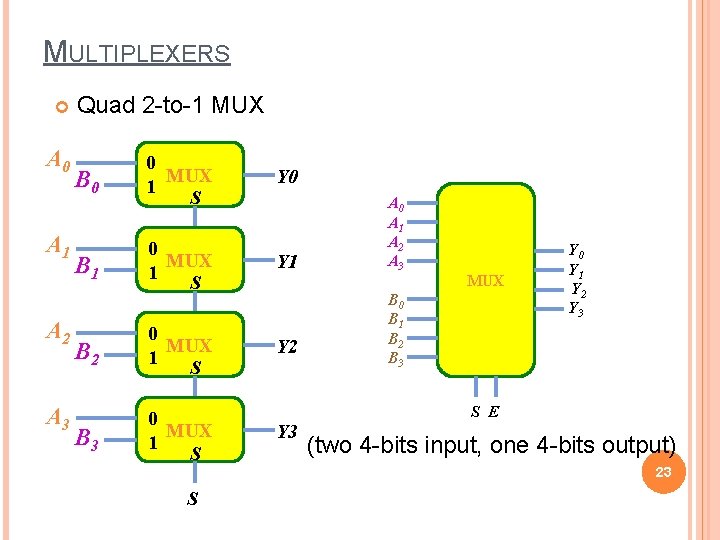
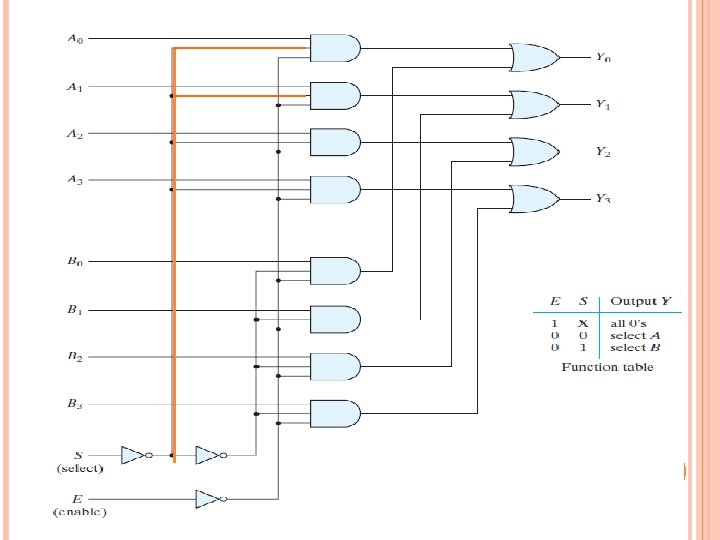
MULTIPLEXERS A 0 A 1 A 2 A 3 Quad 2 -to-1 MUX B 0 0 MUX 1 S B 1 0 MUX 1 S Y 1 B 2 0 MUX 1 S Y 2 B 3 0 MUX 1 S Y 0 Y 3 A 0 A 1 A 2 A 3 MUX B 0 B 1 B 2 B 3 Y 0 Y 1 Y 2 Y 3 S E (two 4 -bits input, one 4 -bits output) 23 S
24
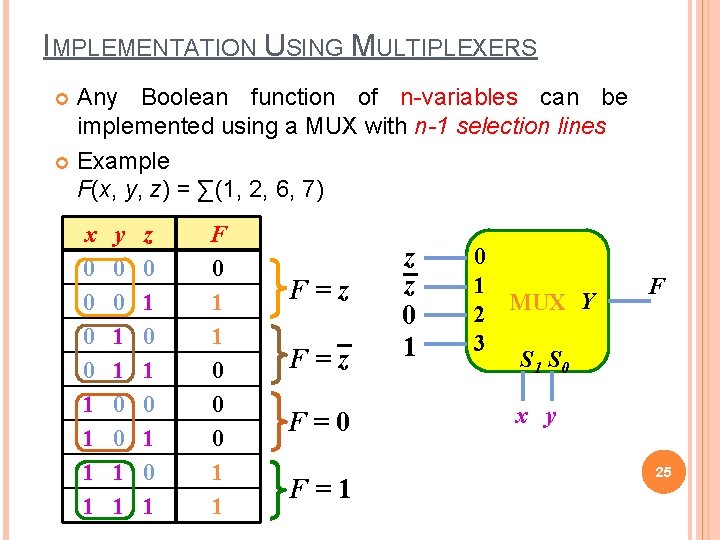
IMPLEMENTATION USING MULTIPLEXERS Any Boolean function of n-variables can be implemented using a MUX with n-1 selection lines Example F(x, y, z) = ∑(1, 2, 6, 7) x 0 0 1 1 y 0 0 1 1 z 0 1 0 1 F 0 1 1 0 0 0 1 1 F=z F=0 F=1 z z 0 1 MUX Y 2 3 S 1 S 0 F x y 25
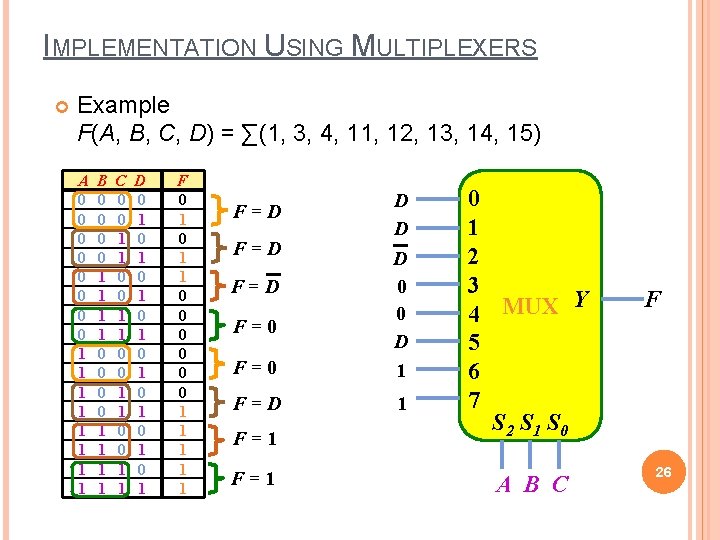
IMPLEMENTATION USING MULTIPLEXERS Example F(A, B, C, D) = ∑(1, 3, 4, 11, 12, 13, 14, 15) A 0 0 0 0 1 1 1 1 B 0 0 0 0 1 1 1 1 C 0 0 1 1 D 0 1 0 1 F 0 1 1 0 0 0 1 1 1 F=0 D D D 0 0 D 1 F=D F=D F=0 F=1 0 1 2 3 Y MUX 4 5 6 7 S 2 S 1 S 0 A B C F 26
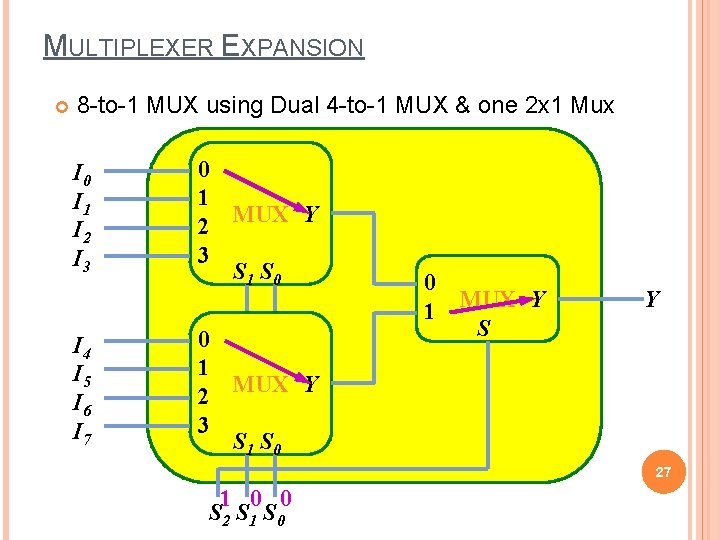
MULTIPLEXER EXPANSION 8 -to-1 MUX using Dual 4 -to-1 MUX & one 2 x 1 Mux I 0 I 1 I 2 I 3 I 4 I 5 I 6 I 7 0 1 MUX Y 2 3 S 1 S 0 0 1 MUX Y S Y 27 1 0 0 S 2 S 1 S 0
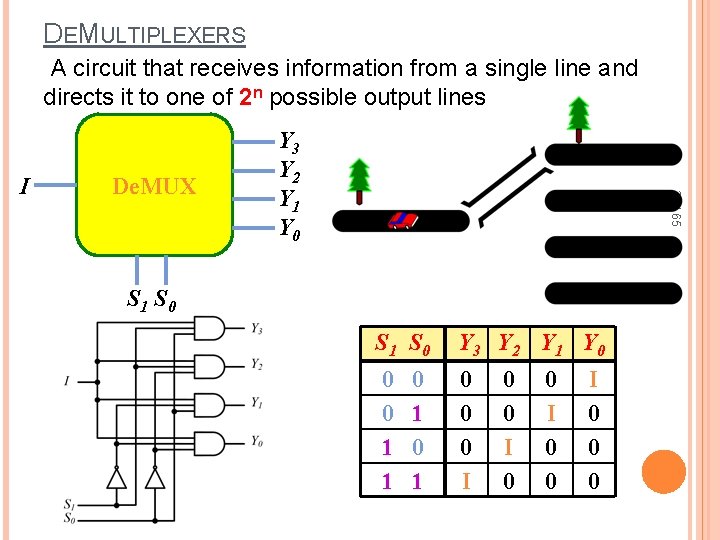
DEMULTIPLEXERS A circuit that receives information from a single line and directs it to one of 2 n possible output lines De. MUX 28 / 65 I Y 3 Y 2 Y 1 Y 0 S 1 S 0 Y 3 Y 2 Y 1 Y 0 0 0 1 1 0 0 0 I 0 1 0 0 I 0 0 0
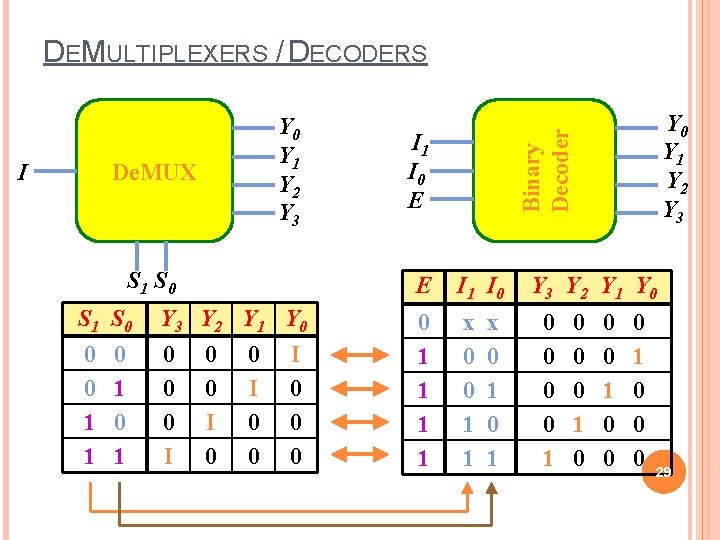
DEMULTIPLEXERS / DECODERS De. MUX I S 1 S 0 Y 3 Y 2 Y 1 Y 0 0 0 1 1 0 0 0 I 0 1 0 0 I 0 0 0 Y 1 Y 2 Y 3 Binary Decoder Y 0 Y 1 Y 2 Y 3 I 1 I 0 E E I 1 I 0 0 1 1 x 0 1 Y 3 Y 2 Y 1 Y 0 0 0 1 0 0 0 29

THE PROBLEMS: 4. 1, 4. 2, 4. 4, 4. 13, 4. 21, 4. 23, 4. 25, 4. 27, 4. 31, 4. 33, 4. 34, 4. 35(a) 30
- Slides: 30