Chapter Five Stoichiometry Chemical Calculations Molecular Masses and

Chapter Five Stoichiometry: Chemical Calculations

Molecular Masses and Formula Masses • Molecular mass: sum of the masses of the atoms represented in a molecular formula. • Simply put: it is the mass of a molecule. • Molecular mass is specifically for molecules. • Ionic compounds don’t exist as molecules; for them we use … • Formula mass: sum of the masses of the atoms or ions present in a formula unit.

Example 5. 1 Calculate the molecular mass of glycerol (1, 2, 3 -propanetriol). Solution In glycerol, one –OH group replaces one H atom on each of the three C atoms in propane, leading to the condensed structural formula CH 2 OH – CHOH - CH 2 OH which translates to the molecular formula C 3 H 8 O 3. To obtain the molecular mass, we must add together three times the atomic mass of carbon, eight times the atomic mass of hydrogen, and three times the atomic mass of oxygen: 3 x atomic mass of C = 3 x 12. 011 u = 36. 033 u 8 x atomic mass of H = 8 x 1. 00794 u = 8. 06352 u 3 x atomic mass of O = 3 x 15. 9994 u = 47. 9982 u Molecular mass of C 3 H 8 O 3 = 92. 095 u

Example 5. 2 Calculate the formula mass of ammonium sulfate, a fertilizer commonly used by home gardeners. Solution Ammonium sulfate is an ionic compound consisting of ammonium ions (NH 4+) and sulfate ions (SO 42–); its formula is therefore (NH 4)2 SO 4. To derive a formula mass from a complex formula like this one, we must make certain that all the atoms in the formula unit are accounted for, which means paying particular attention to all the subscripts and parentheses in the formula. Let’s first note the relevant atomic masses and the way in which they must be combined:

Calculate the formula mass of ammonium sulfate, a fertilizer commonly used by home gardeners. • Summing the atomic masses • (NH 4) 2 : [14. 0067 u + 4 x 1. 00794 u)] x 2 = 36. 0769 u • SO 4 : 32. 066 u + (4 x 15. 9994 u) = 96. 064 u • Formula mass of (NH 4)2 SO 4 = 132. 141 u Assessment As long as every atom in the formula unit is accounted for, we can check our answer by using a different summation, for example, by considering each element separately: Formula mass = (2 x atomic mass N) + (8 x atomic mass H) + (1 x atomic mass of S) + (4 x atomic mass O) = (2 x 14. 0067 u) + (8 x 1. 00794 u) + (1 x 32. 066 u) + (4 x 15. 9994 u) = 132. 141 u

5. 2 The Mole & Avogadro’s Number • Mole (mol): amount of substance that contains as many elementary entities, as there atoms in exactly 12 g of the carbon-12 isotope. • Atoms are small, so this is a BIG number … • Avogadro’s number (NA) = 6. 022 × 1023 mol– 1 • 1 mol = 6. 022 × 1023 “things” (atoms, molecules, ions, formula units, oranges, etc. ) – A mole of oranges would weigh about as much as the earth! • Mole is NOT abbreviated as either M or m (but mol).

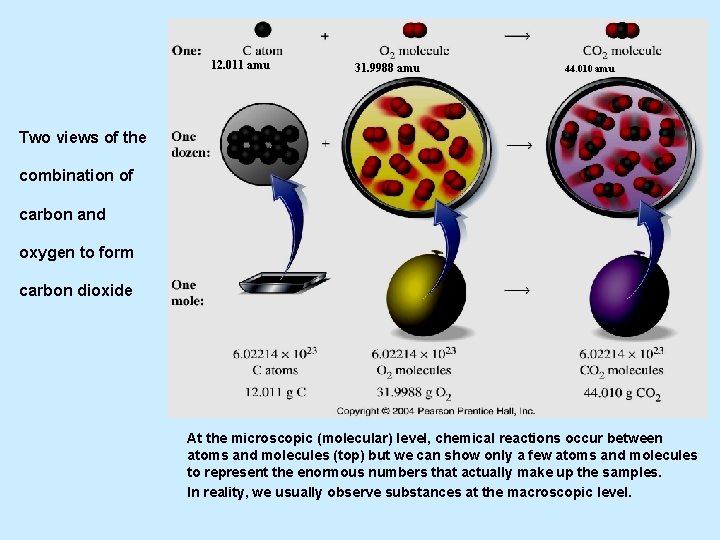
12. 011 amu 31. 9988 amu 44. 010 amu Two views of the combination of carbon and oxygen to form carbon dioxide At the microscopic (molecular) level, chemical reactions occur between atoms and molecules (top) but we can show only a few atoms and molecules to represent the enormous numbers that actually make up the samples. In reality, we usually observe substances at the macroscopic level.

One Mole of Four Elements One mole each of helium, sulfur, copper, and mercury. How many atoms of helium are present? Of sulfur? Of copper? Of mercury?

Example 5. 3 Determine (a) the mass of a 0. 0750 -mol sample of Na, (b) the number of moles of Na in a 62. 5 -g sample, (c) the mass of a sample of Na containing 1. 00 x 1025 Na atoms, and (d) the mass of a single Na atom. Solution (a) To convert from moles to grams, we need to the conversion factor: 22. 99 g Na / 1 mol Na: (b) This time we write the conversion factor as the inverse— 1 mol Na / 22. 99 g Na - because we are to convert from grams to moles:

(c) the mass of a sample of Na containing 1. 00 x 1025 Na atoms, and (c) Here we can use conversion factors, to convert first from number of atoms to number of moles, and then from moles to the mass in grams: Alternatively, we can use the conversion factor 22. 99 g Na/6. 022 x 1023 Na atoms, to convert directly from number of atoms to mass in grams:

(d) the mass of a single Na atom. (d) The answer must have the unit grams per sodium atom (g/Na atom). We know these quantities from the molar mass (22. 99 g Na / mol Na) and Avogadro’s number (1 mol Na / 6. 022 x 1023 atoms). Our answer is the product of these two factors:

The Mole and Molar Mass • Molar mass is the mass of one mole of a substance. • Molar mass is numerically equal to atomic mass, molecular mass, or formula mass. However … • … the units of molar mass are grams (g/mol). • Examples: 1 atom Na = 22. 99 u 1 mol Na = 22. 99 g 1 molecule CO 2 = 44. 01 u 1 mol CO 2 = 44. 01 g 1 formula unit KCl = 74. 56 u 1 mol KCl = 74. 56 g

Conversions involving Mass, Moles, and Number of Atoms/Molecules 1 mol Na = 6. 022 × 1023 Na atoms = 22. 99 g Na We can use these equalities to construct conversion factors, such as: 1 mol Na ––––– 22. 99 g Na ––––– 1 mol Na ––––––––– 6. 022 × 1023 Na atoms 22. 99 g Na ––––––––– 6. 022 × 1023 Na atoms

We can read formulas in terms of moles of atoms or ions.

Example 5. 4 Determine (a) the number of NH 4+ ions in a 145 -g sample of (NH 4)2 SO 4 and (b) the volume of 1, 2, 3 -propanetriol (glycerol) (d = 1. 261 g/m. L) that contains 1. 00 mol O atoms.

a) the number of NH 4+ ions in a 145 -g sample of (NH 4)2 SO 4 and Solution (a) In this calculation, we must use the relationship between the NH 4+ ion and the (NH 4)2 SO 4 formula unit; (132. 14 g / mol) that is, 2 mol NH 4+ / 1 mol (NH 4)2 SO 4. The path to the desired answer is

b) the volume of 1, 2, 3 -propanetriol (glycerol, d = 1. 261 g/m. L) that contains 1. 00 mol O atoms. (b) The conversion factors needed for this calculation are (1) the relationship between moles of O atoms and C 3 H 8 O 3 molecules, (2) the molar mass of C 3 H 8 O 3, and (3) the inverse of the density of C 3 H 8 O 3:

Example 5. 5 An Estimation Example Which of the following is a reasonable value for the number of atoms in 1. 00 g of helium? (a) 4. 1 × 10– 25 (b) 4. 0 (c) 1. 5 × 1023 (d) 1. 5 × 1024

number of atoms in 1. 00 g of helium? a) 4. 1 × 10– 25 b)4. 0 c) 1. 5 × 1023 (d) 1. 5 × 1024 (a) is what we get if, in error, we divide the number of moles of He, 0. 25, by Avogadro’s number. Clearly, we can’t have anything less than one atom. (b) expressed as 4. 0 u is the atomic mass of He; expressed as 4. 0 g/mol He, it is the molar mass. In either case, it is far too small or big to be the number of atoms for any macroscopic sample. (c) is the correct order of magnitude, and the correct answer. (d) Order of magnetude is reasonable, however, it is larger than Avogadro’s number. We would expect a fraction of a mole of helium to have fewer than Avogadro’s number of atoms. Response (c) is the correct answer, obtained from the calculation: 0. 25 x NA.

5. 4 Mass Percent Composition from Chemical Formulas The mass percent composition of a compound refers to the proportion of the constituent elements, expressed as the number of grams of each element per 100 grams of the compound. In other words … X g element X % element = ––––––– 100 g compound OR … g element % element = –––––– × 100 g compound

Percentage Composition of Butane

Example 5. 6 Calculate, to four significant figures, the mass percent of each element in ammonium nitrate (NH 4 NO 3).

Calculate, to four significant figures, the mass percent of each element in ammonium nitrate NH 4 NO 3. Solution

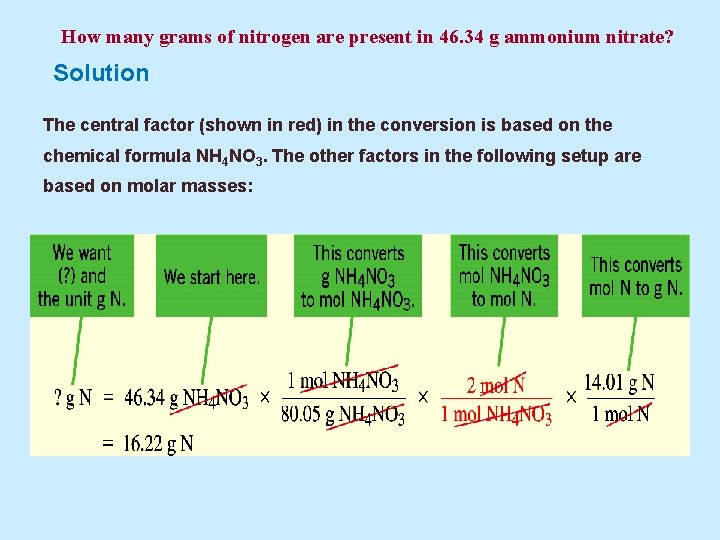
Example 5. 7 How many grams of nitrogen are present in 46. 34 g ammonium nitrate?

How many grams of nitrogen are present in 46. 34 g ammonium nitrate? Solution The central factor (shown in red) in the conversion is based on the chemical formula NH 4 NO 3. The other factors in the following setup are based on molar masses:

Example 5. 8 An Estimation Example Without doing detailed calculations, determine which of these compounds contains the greatest mass of sulfur per gram of compound: barium sulfate, (Ba. SO 4) lithium sulfate, (Li 2 SO 4) sodium sulfate, (Na 2 SO 4) lead sulfate. (Pb. SO 4)

The Periodic table

the greatest mass of sulfur per gram of compound: a) barium sulfate, b) lithium sulfate, c) sodium sulfate, d) lead sulfate. Analysis and Conclusions To make this comparison, we need formulas of the compounds, which we can get from their names: Ba. SO 4 Li 2 SO 4 Na 2 SO 4 Pb. SO 4 The compound with the greatest mass of sulfur per gram of compound also has the greatest mass of sulfur per 100 g of compound—in other words, the greatest % S by mass. From the formulas, we see that in one mole of each compound there is one mole of sulfur, which means 32. 066 g S. Thus, the compound with the greatest % S is the one with the smallest formula mass. Because each formula unit has one SO 42– ion, all we have to do is compare some atomic masses: that of barium to twice that of lithium, and so on. With just a glance at an atomic mass table: we see the answer must be lithium sulfate, Li 2 SO 4.

5. 5 Chemical Formulas from Mass Percent Composition • We can “reverse” the process of finding percentage composition. • First we use the percentage or mass of each element to find moles of each element. • Then we can obtain the empirical formula by finding the smallest whole-number ratio of moles. – Find the whole-number ratio by dividing each number of moles by the smallest number of moles.

Example 5. 9 Phenol, a general disinfectant, has the composition 76. 57% C, 6. 43% H, and 17. 00% O by mass. Determine its empirical formula.

the composition 76. 57% C, 6. 43% H, and 17. 00% O by mass. Determine its empirical formula. Solution Step 1: A 100. 00 -g sample of phenol contains 76. 57 g C, 6. 43 g H, and 17. 00 g O. Step 2: We convert the masses of C, H, and O to amounts in moles:

the composition 76. 57% C, 6. 43% H, and 17. 00% O by mass. Determine its empirical formula. Step 3: Now we use the numbers of moles in Step 2 as subscripts in a tentative formula: C 6. 375 H 6. 38 O 1. 063 Step 4: Next we divide each subscript by the smallest (1. 063) to try to get integral subscripts: Step 5: The subscripts in Step 4 are all integers. We need do nothing further. The empirical formula of phenol is C 6 H 6 O.

Example 5. 10 Diethylene glycol, used in antifreeze, as a softening agent for textile fibers and some leathers, and as a moistening agent for glues and paper, has the composition 45. 27% C, 9. 50% H, and 45. 23% O by mass. Determine its empirical formula.

the composition 45. 27% C, 9. 50% H, and 45. 23% O by mass. Determine its empirical formula. Solution Step 1: A 100. 00 -g sample of diethylene glycol contains 45. 27 g C, 9. 50 g H, and 45. 23 g O. Step 2: We convert the masses of C, H, and O to amounts in moles:

the composition 45. 27% C, 9. 50% H, and 45. 23% O by mass. Determine its empirical formula. Step 3: Now we use the numbers of moles in Step 2 as subscripts in a tentative formula: C 3. 769 H 9. 42 O 2. 827 Step 4: Next we must divide each subscript by the smallest (2. 827) in an attempt to get integral subscripts: Step 5: Finally we multiply all the subscripts from Step 4 by a common factor to convert them all to integers. By recognizing that 1. 333 = 4/3 and 3. 33 = 10/3, we can see that the common factor we need is 3:

Relating Molecular Formulas to Empirical Formulas • A molecular formula is a simple integer multiple of the empirical formula. • That is, an empirical formula of CH 2 means that the molecular formula is CH 2, or C 2 H 4, or C 3 H 6, or C 4 H 8, etc. • So: we find the molecular formula by: molecular formula mass empirical formula mass = integer (nearly) We then multiply each subscript in the empirical formula by the integer.

Example 5. 11 The empirical formula of hydroquinone, a chemical used in photography, is C 3 H 3 O, and its molecular mass is 110 u. What is its molecular formula?

The empirical formula of hydroquinone, is C 3 H 3 O, and its molecular mass is 110 u. What is its molecular formula? Solution The empirical formula mass is (3 x 12. 0 u) + (3 x 1. 0 u) + 16. 0 u = 55. 0 u. The multiplier we need to convert the subscripts in the empirical formula to those in the molecular formula is the integral factor The molecular formula is (C 3 H 3 O)2 , or C 6 H 6 O 2.

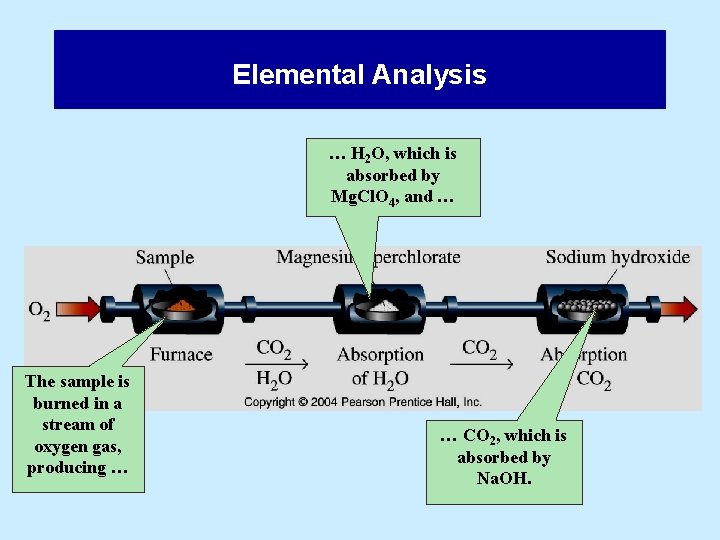
5. 6 Elemental Analysis … • … is one method of determining empirical formulas in the laboratory. • This method is used primarily for simple organic compounds (that contain carbon, hydrogen, oxygen). – The organic compound is burned in oxygen. – The products of combustion (usually CO 2 and H 2 O) are weighed. – The amount of each element is determined from the mass of products.

Elemental Analysis … H 2 O, which is absorbed by Mg. Cl. O 4, and … The sample is burned in a stream of oxygen gas, producing … … CO 2, which is absorbed by Na. OH.

Example 5. 12 Burning a 0. 1000 -g sample of a carbon–hydrogen–oxygen compound in oxygen yields 0. 1953 g CO 2 and 0. 1000 g H 2 O. A separate experiment shows that the molecular mass of the compound is 90 u. Determine (a) the mass percent composition, (b) the empirical formula, and (c) the molecular formula of the compound.

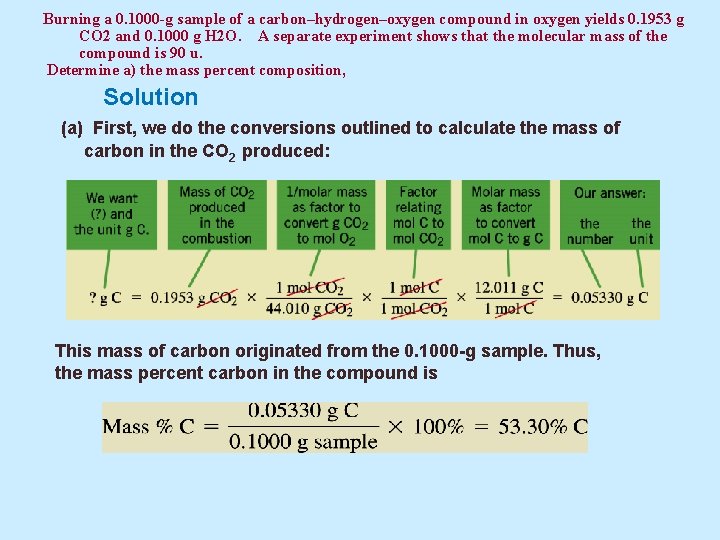
Burning a 0. 1000 -g sample of a carbon–hydrogen–oxygen compound in oxygen yields 0. 1953 g CO 2 and 0. 1000 g H 2 O. A separate experiment shows that the molecular mass of the compound is 90 u. Determine a) the mass percent composition, Solution (a) First, we do the conversions outlined to calculate the mass of carbon in the CO 2 produced: This mass of carbon originated from the 0. 1000 -g sample. Thus, the mass percent carbon in the compound is

Burning a 0. 1000 -g sample of a carbon–hydrogen–oxygen compound in oxygen yields 0. 1953 g CO 2 and 0. 1000 g H 2 O. A separate experiment shows that the molecular mass of the compound is 90 u. Determine a) the mass percent composition, We can use similar calculations to determine first the mass of hydrogen and then the mass percent of hydrogen in the compound: Finally, we can calculate the mass percent oxygen by subtracting the mass percents of C and H from 100. 00%: % O = 100. 00% – 53. 30% – 11. 19% = 35. 51% Therefore the mass percent composition is 53. 30% C, 11. 19% H and 35. 51% O

Burning a 0. 1000 -g sample of a carbon–hydrogen–oxygen compound in oxygen yields 0. 1953 g CO 2 and 0. 1000 g H 2 O. A separate experiment shows that the molecular mass of the compound is 90 u. Determine b) the empirical formula, (b) Here we apply the method of Examples 3. 9 and 3. 10, but we need only the first four steps. Step 1: A 100. 00 -g sample of the compound contains 53. 30 g C, 11. 19 g H, and 35. 51 g O. Step 2: We convert the masses of C, H, and O to numbers of moles:

Burning a 0. 1000 -g sample of a carbon–hydrogen–oxygen compound in oxygen yields 0. 1953 g CO 2 and 0. 1000 g H 2 O. A separate experiment shows that the molecular mass of the compound is 90 u. Determine b) the empirical formula, and c) the molecular formula of the compound. Step 3: Next, we use the numbers of moles in Step 2 as subscripts in a tentative formula: C 4. 438 H 11. 10 O 2. 220 Step 4: We divide all subscripts by the smallest subscript (2. 220) to get integral subscripts: • c) The empirical formula mass is (2 x 12. 0 u) + (5 x 1. 0 u) + 16. 0 u = 45. 0 u. The multiplier we need to convert the subscripts in the empirical formula to those in the molecular formula is the integral factor The molecular formula is (C 2 H 5 O)2 , or C 4 H 10 O 2.

5. 7 Writing Chemical Equations • A chemical equation is a shorthand description of a chemical reaction, using symbols and formulas to represent the elements and compounds involved.

Writing Chemical Equations • Sometimes additional information about the reaction is shown in the equation.

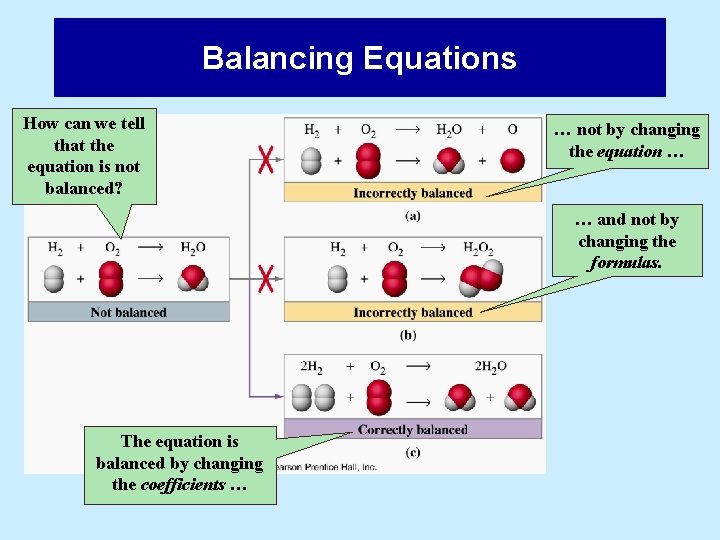
Balancing Equations How can we tell that the equation is not balanced? … not by changing the equation … … and not by changing the formulas. The equation is balanced by changing the coefficients …

Guidelines for Balancing Chemical Equations • If an element is present in just one compound on each side of the equation, try balancing that element first. • Balance any reactants or products that exist as the free element last. • In some reactions, certain groupings of atoms (such as polyatomic ions) remain unchanged. In such cases, treat these groupings as a unit. • At times, an equation can be balanced by first using a fractional coefficient(s). The fraction is then cleared by multiplying each coefficient by a common factor.

Example 5. 13 Balance the equation Fe + O 2 Fe 2 O 3 (not balanced)

Fe + O 2 Fe 2 O 3 (not balanced) Solution It seems that the easiest place to begin is with the iron atoms. There is one on the left (Fe) and two on the right (Fe 2 O 3), and we can balance them by placing the coefficient 2 on the left: 2 Fe + O 2 Fe 2 O 3 (Fe balanced, O not balanced) To balance the oxygen atoms, we begin by noting that there are two of them on the left and three on the right. An easy way to get three O atoms on the left, thereby balancing the equation, is to use the fractional coefficient 3/2 before O 2 on the left {3/2 x 2 = 3}: 2 Fe + 3/2 O 2 Fe 2 O 3 (balanced, fractional coefficient)

Fe + O 2 Fe 2 O 3 (not balanced) Solution Fractional coefficients are not only acceptable in equations, sometimes they are desirable. If we don’t want them, however, we can easily clear an equation of them by multiplying every coefficient by the smallest integer required to clear the fractions, in this case, 2: 2 x {2 Fe + 3/2 O 2 Fe 2 O 3} becomes 4 Fe + 3 O 2 2 Fe 2 O 3 (balanced, coefficients integral)

Example 5. 14 Balance the equation C 2 H 6 + O 2 CO 2 + H 2 O

Solution C 2 H 6 + O 2 CO 2 + H 2 O Oxygen appears as the free element on the left, so let’s leave it for last and balance the other two elements first. To balance carbon, we place the coefficient 2 in front of CO 2: C 2 H 6 + O 2 2 CO 2 + H 2 O (C balanced, H and O not balanced) To balance hydrogen, we need the coefficient 3 before H 2 O: C 2 H 6 + O 2 2 CO 2 + 3 H 2 O (C and H balanced, O not balanced)

C 2 H 6 + O 2 CO 2 + H 2 O Solution Now, if we count oxygen atoms, we find two on the left and seven on the right. We can get seven on each side by using the fractional coefficient 7/2 (7/2 x 2 = 7): C 2 H 6 + 7/2 O 2 2 CO 2 + 3 H 2 O (balanced) To obtain integral coefficients, we multiply each coefficient by 2: 2 x {C 2 H 6 + 7/2 O 2 2 CO 2 + 3 H 2 O} That leads to 2 C 2 H 6 + 7 O 2 4 CO 2 + 6 H 2 O (balanced)

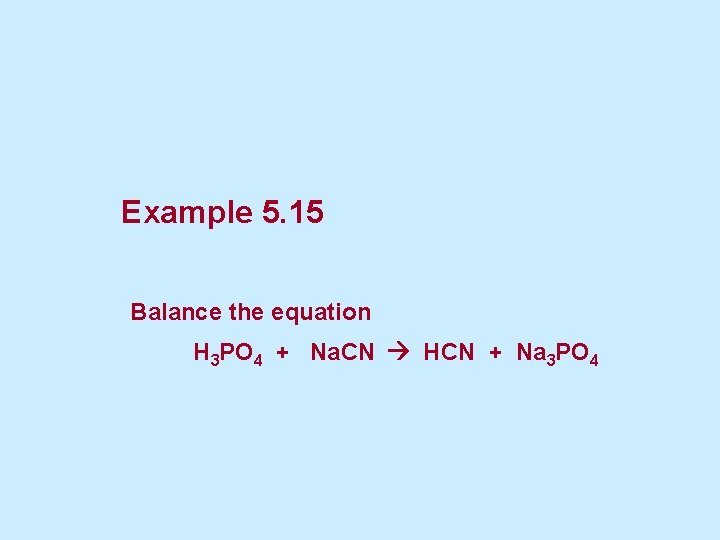
Example 5. 15 Balance the equation H 3 PO 4 + Na. CN HCN + Na 3 PO 4

H 3 PO 4 + Na. CN HCN + Na 3 PO 4 Solution Notice that the PO 4 and CN groups remain unchanged in the reaction. For purposes of balancing equations, we can often treat such groups as a whole, rather than breaking them down into their constituent atoms. To balance hydrogen atoms, we place a 3 before HCN: H 3 PO 4 + Na. CN 3 HCN + Na 3 PO 4 (not balanced) To balance cyanide ions, we put a 3 in front of the Na. CN. Doing this also balances the sodium ions: H 3 PO 4 + 3 Na. CN 3 HCN + Na 3 PO 4 (balanced) Because the PO 4 was balanced to begin with and we did nothing to upset that balance, we are finished; the equation is balanced.

Example 5. 16 A Conceptual Example Write a reasonable chemical equation for the reaction between water and a liquid molecular chloride of phosphorus to form an aqueous solution of hydrochloric acid and phosphorus acid. The phosphorus-chlorine compound is 77. 45% Cl by mass.

chemical equation for the reaction between water and a liquid molecular chloride of phosphorus to form an aqueous solution of hydrochloric acid and phosphorus acid. The phosphorus-chlorine compound is 77. 45% Cl by mass. Analysis and Conclusions Establishing the formula of the chloride of phosphorus. We can form a compound that is 22. 55% P and 77. 45% Cl. A 100. 00 -g sample of the compound consists of 22. 55 g P and 77. 45 g Cl, corresponding to 0. 728 mol P and 2. 185 mol Cl. The formula P 0. 728 Cl 2. 185 reduces to PCl 3. Establishing the formulas of hydrochloric and phosphorus acids. Hydrochloric acid, a binary acid, has the formula HCl. Table 2. 5 gives H 3 PO 4 as the formula of phosphoric acid. Phosphorus acid should have one O atom fewer per molecule than the “-ic” acid, giving the formula H 3 PO 3.

chemical equation for the reaction between water and a liquid molecular chloride of phosphorus to form an aqueous solution of hydrochloric acid and phosphorus acid. The phosphorus-chlorine compound is 77. 45% Cl by mass. Analysis and Conclusions Writing and balancing the equation. The unbalanced equation, including an indication of the physical form of each substance, is PCl 3(l) + H 2 O(l) HCl(aq) + H 3 PO 3(aq) The balanced equation requires the coefficient 3 for H 2 O(l) and for HCl(aq): PCl 3(l) + 3 H 2 O(l) 3 HCl(aq) + H 3 PO 3(aq)

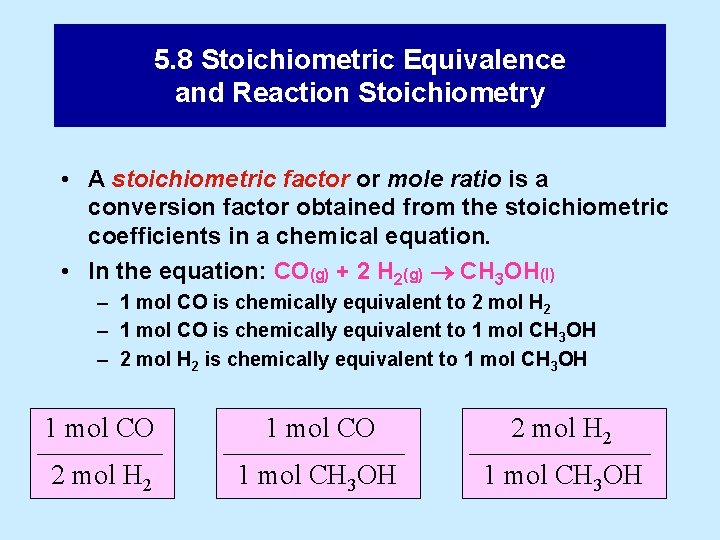
5. 8 Stoichiometric Equivalence and Reaction Stoichiometry • A stoichiometric factor or mole ratio is a conversion factor obtained from the stoichiometric coefficients in a chemical equation. • In the equation: CO(g) + 2 H 2(g) CH 3 OH(l) – 1 mol CO is chemically equivalent to 2 mol H 2 – 1 mol CO is chemically equivalent to 1 mol CH 3 OH – 2 mol H 2 is chemically equivalent to 1 mol CH 3 OH 1 mol CO ––––– 2 mol H 2 1 mol CO ––––––– 1 mol CH 3 OH 2 mol H 2 ––––––– 1 mol CH 3 OH

Outline of Simple Reaction Stoichiometry

Example 5. 17 When 0. 105 mol propane is burned in an excess of oxygen, how many moles of oxygen are consumed? The reaction is C 3 H 8 + 5 O 2 3 CO 2 + 4 H 2 O

When 0. 105 mol propane is burned in an excess of oxygen, how many moles of oxygen are consumed? The reaction is C 3 H 8 + 5 O 2 3 CO 2 + 4 H 2 O Solution The stoichiometric coefficients in the equation allow us to write the equivalence From this equivalence, we can derive two conversion factors: Because we are given the number of moles of propane (substance A in Figure 3. 8) and are seeking the number of moles of O 2 consumed (substance B in Figure 3. 8), we need the factor that has the unit “mol O 2” in the numerator and the unit “mol C 3 H 8 ” in the denominator. This is the conversion factor shown in red above:

Example 5. 18 The final step in the production of nitric acid involves the reaction of nitrogen dioxide with water; nitrogen monoxide is also produced. How many grams of nitric acid are produced for every 100. 0 g of nitrogen dioxide that reacts?

How many grams of nitric acid are produced for every 100. 0 g of nitrogen dioxide that reacts? Solution 5. 18 Because no equation is given, we must first write a chemical equation from the description of the reaction. To balance the equation, let’s first balance H atoms because H appears in one reactant and one product. Then we can balance N atoms because they appear on the reactant side only in NO 2. At this point, O atoms will also be balanced.

How many grams of nitric acid are produced for every 100. 0 g of nitrogen dioxide that reacts? Solution 5. 18 continued Now, we convert the mass of the given substance, NO 2, to an amount in moles, using the molar mass. Next, we use coefficients from the balanced equation to establish the stoichiometric equivalence of NO 2 and HNO 3

How many grams of nitric acid are produced for every 100. 0 g of nitrogen dioxide that reacts? Solution 5. 18 continued Because we need to convert from moles of NO 2 to moles of HNO 3, we should use this equivalence to write the stoichiometric factor needed for the conversion. Finally, we can convert from moles of HNO 3 to grams of HNO 3 using its molar mass.

How many grams of nitric acid are produced for every 100. 0 g of nitrogen dioxide that reacts? Solution 5. 18 in one equation ? g HNO 3 = 100. 0 g NO 2 convert to moles HNO 3 (2/3) convert to g HNO 3

Example 5. 19 Ammonium sulfate, a common fertilizer used by gardeners, is produced commercially by passing gaseous ammonia into an aqueous solution that is 65% H 2 SO 4 by mass and has a density of 1. 55 g/m. L. How many milliliters of this sulfuric acid solution are required to convert 1. 00 kg NH 3 to (NH 4)2 SO 4 ?

Ammonium sulfate produced by passing gaseous ammonia into an aqueous solution that is 65% H 2 SO 4 by mass, and has a density of 1. 55 g/m. L. How many milliliters of this sulfuric acid solution are required to convert 1. 00 kg NH 3 to (NH 4)2 SO 4? Solution 5. 19 First, we must write the balanced equation for the reaction: 2 NH 3(g) + H 2 SO 4(aq) (NH 4)2 SO 4(aq) The required setup has 1. 00 kg NH 3 —the given substance—as its starting point. Because we are seeking a volume of H 2 SO 4(aq), the setup has the general form ? m. L H 2 SO 4(aq) = 1. 00 kg NH 3 x conversion factors

Ammonium sulfate produced by passing gaseous ammonia into an aqueous solution that is 65% H 2 SO 4 by mass, and has a density of 1. 55 g/m. L. How many milliliters of this sulfuric acid solution are required to convert 1. 00 kg NH 3 to (NH 4)2 SO 4? Solution 5. 19 continued We begin by converting kilograms of NH 3 to grams of NH 3. Then we can apply the flow chart below to find grams of H 2 SO 4. Finally, we use the percent composition and then the density of the H 2 SO 4(aq) to convert from grams of H 2 SO 4 to milliliters of H 2 SO 4(aq):

Ammonium sulfate produced by passing gaseous ammonia into an aqueous solution that is 65% H 2 SO 4 by mass, and has a density of 1. 55 g/m. L. How many milliliters of this sulfuric acid solution are required to convert 1. 00 kg NH 3 to (NH 4)2 SO 4? Solution 5. 19 continued In the combined setup, the conversions are done in the order in which they are described above:

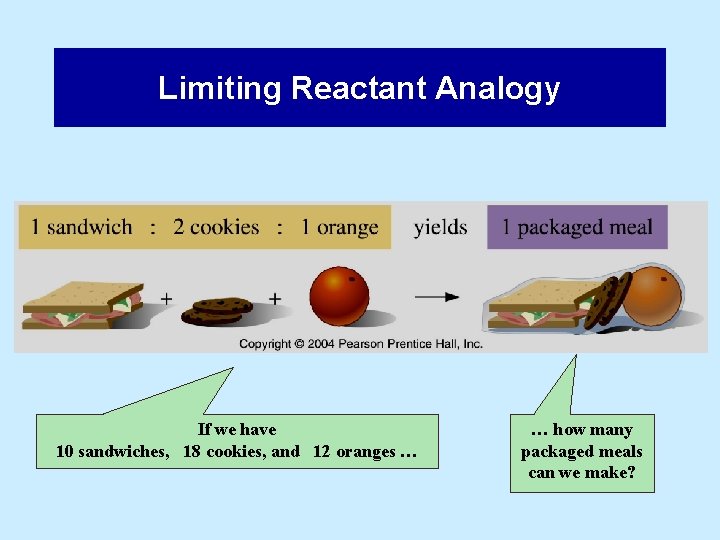
5. 9 Limiting Reactants • Many reactions are carried out with a limited amount of one reactant and a plentiful amount of the other(s). • The reactant that is completely consumed in the reaction, limits the amounts of products and is called the limiting reactant, or limiting reagent. • The limiting reactant is not necessarily the one present in smallest amount.

Limiting Reactant Analogy If we have 10 sandwiches, 18 cookies, and 12 oranges … … how many packaged meals can we make?

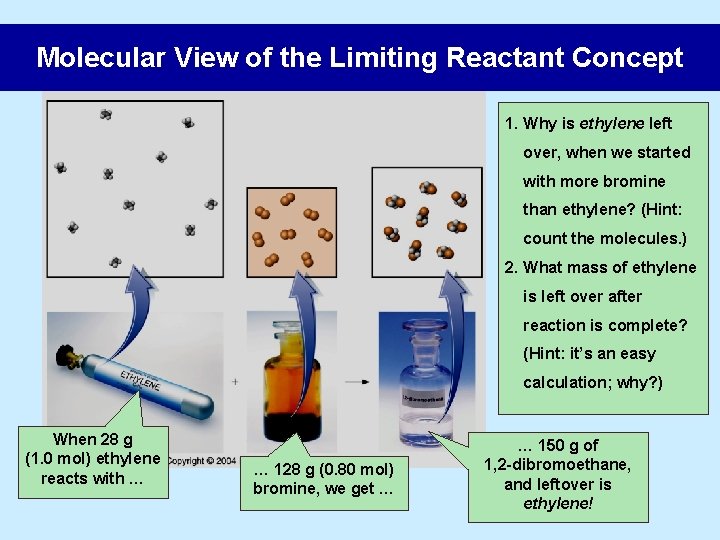
Molecular View of the Limiting Reactant Concept 1. Why is ethylene left over, when we started with more bromine than ethylene? (Hint: count the molecules. ) 2. What mass of ethylene is left over after reaction is complete? (Hint: it’s an easy calculation; why? ) When 28 g (1. 0 mol) ethylene reacts with … … 128 g (0. 80 mol) bromine, we get … … 150 g of 1, 2 -dibromoethane, and leftover is ethylene!

Recognizing and Solving Limiting Reactant Problems • We recognize limiting reactant problems by the fact that amounts of two (or more) reactants are given. • One way to solve them is to perform a normal stoichiometric calculation of the amount of product obtained, starting with each reactant. • The reactant that produces the smallest amount of product is the limiting reactant.

Example 5. 20 Magnesium nitride Mg 3 N 2 can be formed by the reaction of magnesium metal with nitrogen gas. (a) How many grams of magnesium nitride can be made in the reaction of 35. 00 g of magnesium and 15. 00 g of nitrogen? (b) How many grams of the excess reactant remain after the reaction?

How many grams of magnesium nitride can be made in the reaction of 35. 00 g of magnesium and 15. 00 g of nitrogen? How many grams of the excess reactant remain after the reaction? Solution 5. 20 (a) As usual, we must first write a balanced equation. We can identify the limiting reactant by finding the number of moles of Mg 3 N 2(s) produced by assuming first one reactant, and then the other is the limiting reactant.

How many grams of magnesium nitride can be made in the reaction of 35. 00 g of magnesium and 15. 00 g of nitrogen? How many grams of the excess reactant remain after the reaction? -) Assuming Mg is the limiting reactant and N 2 is in excess: -) Assuming N 2 is the limiting reactant and Mg is in excess: Because the amount of product in the first calculation (0. 4800 mol Mg 3 N 2) is smaller than that in the second (0. 5355 mol Mg 3 N 2), we know that magnesium is the limiting reactant.

How many grams of magnesium nitride can be made in the reaction of 35. 00 g of magnesium and 15. 00 g of nitrogen? How many grams of the excess reactant remain after the reaction? Solution 5. 20 continued When 0. 4800 mol Mg 3 N 2 has been formed, the Mg is completely consumed and the reaction stops, producing a specific mass of Mg 3 N 2.

How many grams of magnesium nitride can be made in the reaction of 35. 00 g of magnesium and 15. 00 g of nitrogen? How many grams of the excess reactant remain after the reaction? Solution 5. 20 continued (b) Having found that the amount of product is 0. 4800 mol Mg 3 N 2, we can now calculate how much N 2 must have been consumed. From this, we calculate the mass of excess N 2.

5. 10 Yields of Chemical Reactions • The theoretical yield of a chemical reaction is the calculated quantity of product in the reaction. • The actual yield is the amount you actually get when you carry out the reaction. • Actual yield will be less than theoretical yield, for many reasons … can you name some? actual yield Percent yield = ––––––– × 100 theoretical yield

Example 5. 21 Ethyl acetate is a solvent used as fingernail polish remover. What mass of acetic acid is needed to prepare 252 g ethyl acetate if the expected percent yield is 85. 0%? Assume that the other reactant, ethanol, is present in excess and water is the by-product. The equation for the reaction, carried out in the presence of H 2 SO 4, is CH 3 COOH + HOCH 2 CH 3 Acetic acid Ethanol CH 3 COOCH 2 CH 3 Ethyl acetate + H 2 O

What mass of acetic acid is needed to prepare 252 g ethyl acetate if the expected percent yield is 85. 0%? Solution First, we can solve Equation (3. 8) for theoretical yield and substitute known quantities for the actual and percent yields. Then, we can determine the mass of acetic acid required to produce 296 g ethyl acetate.

Example 3. 22 A Conceptual Example What is the maximum yield of CO(g) obtainable from 725 g of C 6 H 14(l), assuming no other carbon-containing reactant or product is formed?

What is the maximum yield of CO(g) obtainable from 725 g of C 6 H 14 (l), Analysis and Conclusions We can start the calculation by converting grams of C 6 H 14 to moles of C 6 H 14, and we can end it by converting moles of CO to grams of CO. The critical link between these two “ends” of the calculation are the factors that relate moles of C to moles of C 6 H 14 on the one hand moles of CO to moles of C on the other. In the solution equation conversion factors are shown in red. The solution equation is:

5. 11 Solutions and Solution Stoichiometry • Solute: the substance being dissolved. • Solvent: the substance doing the dissolving. • Solution: A mixture of solute and solvent. • Concentration of a solution: the quantity of a solute in a given quantity of solution (or solvent). – A concentrated solution contains a relatively large amount of solute vs. the solvent (or solution). – A dilute solution contains a relatively small concentration of solute vs. the solvent (or solution).

Molar Concentration Molarity (M), or molar concentration, is the amount of solute, in moles, per liter of solution: moles of solute Molarity = ––––––– liters of solution • A solution that is 0. 35 M sucrose contains 0. 35 moles of sucrose in each liter of solution. • Keep in mind that molarity signifies moles of solute per liter of solution, not liters of solvent.

Example 5. 23 What is the molarity of a solution in which 333 g potassium hydrogen carbonate ( KHCO 3 ) is dissolved in enough water to make 10. 0 L of solution?

molarity of a solution in which 333 g potassium hydrogen carbonate is dissolved in enough water to make 10. 0 L of solution? Solution First, let’s prepare the setup that converts mass to number of moles of KHCO 3. Now, without solving this expression, let’s use it (number of moles) as the numerator in the defining equation for molarity. The solution volume, 10. 0 L, is the denominator.

Example 5. 24 We want to prepare a 6. 68 molar solution of Na. OH (6. 68 M Na. OH). (a) How many moles of Na. OH are required to prepare 0. 500 L of 6. 68 M Na. OH? (b) How many liters of 6. 68 M Na. OH can we prepare with 2. 35 kg Na. OH?

(a) How many moles of Na. OH are required to prepare 0. 500 L of 6. 68 M Na. OH? Solution 5. 24 (a) This calculation requires only a one-step conversion from liters of solution to moles of Na. OH, with the molarity of the solution as the conversion factor:

(b) How many liters of 6. 68 M Na. OH can we prepare with 2. 35 kg Na. OH? Solution 5. 24 continued (b) The central conversion factors in this calculation are the inverse of the molar mass of Na. OH to convert from grams of Na. OH to moles of Na. OH and the inverse of the molarity— 1 L soln/6. 68 Na. OH—to convert from moles of Na. OH to liters of solution. We must also convert from kilograms of Na. OH to grams of Na. OH. In all, the required conversions are kg Na. OH mol Na. OH L soln which are set up as follows:

Example 5. 25 The label of a stock bottle of aqueous ammonia indicates that the solution is 28. 0% NH 3 by mass and has a density of 0. 898 g/m. L. Calculate the molarity of the solution.

-) aqueous ammonia indicates that the solution is 28. 0% NH 3 by mass and has a density of 0. 898 g/m. L. Calculate the molarity of the solution. Solution 5. 25

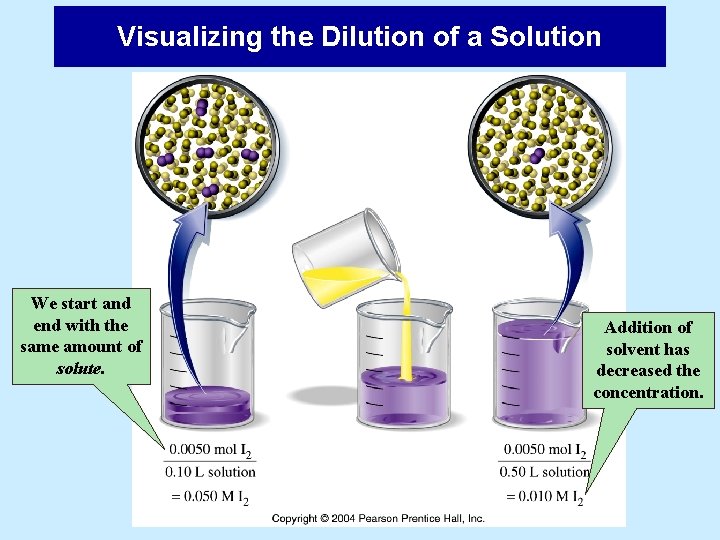
Dilution of Solutions • Dilution is the process of preparing a more dilute solution by adding solvent to a more concentrated one. • Addition of solvent does not change the amount of solute in a solution but does change the solution concentration. • It is very common to prepare a concentrated stock solution of a solute, then dilute it to other concentrations as needed.

Visualizing the Dilution of a Solution We start and end with the same amount of solute. Addition of solvent has decreased the concentration.

Dilution Calculations … • Number of moles of solute does not change on dilution. • Moles of solute = M × V • Therefore … Mconc × Vconc = Mdil × Vdil

Example 5. 26 How many milliliters of a 2. 00 M Cu. SO 4 stock solution are needed to prepare 0. 250 L of 0. 400 M Cu. SO 4?

How many milliliters of a 2. 00 M Cu. SO 4 stock solution are needed to prepare 0. 250 L of 0. 400 M Cu. SO 4? Solution Applying the principle of dilution: The key is to note that all the solute in the unknown volume of the stock solution appears in the 0. 250 L of 0. 400 M Cu. SO 4. a) First, let’s calculate that amount of solute: Now we need to answer the question, “What volume of 2. 00 M Cu. SO 4 contains 0. 100 mol Cu. SO 4? ” In doing so, we will have answered the original question.

How many milliliters of a 2. 00 M Cu. SO 4 stock solution are needed to prepare 0. 250 L of 0. 400 M Cu. SO 4? Solution 5. 26 continued Of course, we could have done all of this in a single step: b) This can also be easily solved by using the dilution equation: Then, we can substitute these terms into the equation:

Solutions in Chemical Reactions • Molarity provides an additional tool in stoichiometric calculations based on chemical equations. • Molarity provides factors for converting between moles of solute (either reactant or product) and liters of solution.

Example 5. 27 A chemical reaction familiar to geologists is that used to identify limestone. The reaction of hydrochloric acid with limestone, which is largely calcium carbonate, is seen through an effervescence —a bubbling due to the liberation of gaseous carbon dioxide: Ca. CO 3(s) + 2 HCl(aq) Ca. Cl 2(aq) + H 2 O(l) + CO 2(g) How many grams of Ca. CO 3(s) are consumed in a reaction with 225 m. L of 3. 25 M HCl?

Ca. CO 3(s) + 2 HCl(aq) Ca. Cl 2(aq) + H 2 O(l) + CO 2(g) How many grams of Ca. CO 3(s) are consumed in a reaction with 225 m. L of 3. 25 M HCl? Solution

Cumulative Example The combustion in oxygen of 1. 5250 g of an alkane-derived compound composed of carbon, hydrogen, and oxygen yields 3. 047 g CO 2 and 1. 247 g H 2 O. The molecular mass of this compound is 88. 1 u. Draw a plausible structural formula for this compound. Is there more than one possibility? Explain.

The combustion in oxygen of 1. 5250 g of an alkane-derived compound composed of carbon, hydrogen, and oxygen yields 3. 047 g CO 2 and 1. 247 g H 2 O. The molecular mass of this compound is 88. 1 u. Solution We begin by finding the moles of carbon in 3. 047 g of CO 2 and the moles of hydrogen in 1. 247 g of H 2 O. We will need these numbers of moles for the empirical formula determination later. Next, we convert moles of each element to mass.

The combustion in oxygen of 1. 5250 g of an alkane-derived compound composed of carbon, hydrogen, and oxygen yields 3. 047 g CO 2 and 1. 247 g H 2 O. The molecular mass of this compound is 88. 1 u. We find the mass of oxygen by subtracting the masses of carbon and hydrogen from the sample mass. Then we convert the mass of oxygen to moles. Now we use the moles of carbon, hydrogen, and oxygen to construct a tentative formula.

The combustion in oxygen of 1. 5250 g of an alkane-derived compound composed of carbon, hydrogen, and oxygen yields 3. 047 g CO 2 and 1. 247 g H 2 O. The molecular mass of this compound is 88. 1 u. Then we divide each subscript by the subscript for oxygen (because this is the smallest of the three subscripts). The empirical formula mass is 44. 053 u. Next, we calculate the ratio of the molecular mass to the empirical formula mass.

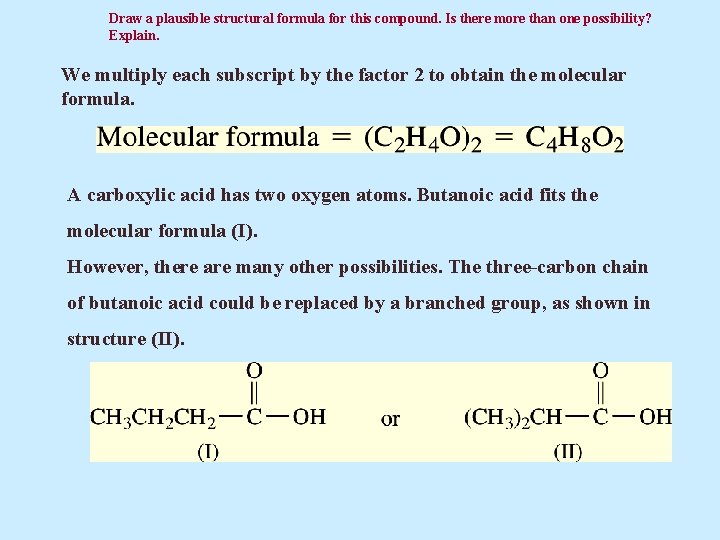
Draw a plausible structural formula for this compound. Is there more than one possibility? Explain. We multiply each subscript by the factor 2 to obtain the molecular formula. A carboxylic acid has two oxygen atoms. Butanoic acid fits the molecular formula (I). However, there are many other possibilities. The three-carbon chain of butanoic acid could be replaced by a branched group, as shown in structure (II).

Is there more than one possibility? Explain. The compounds (III) and (IV) also fit the molecular formula. Another interesting observation is that alkane-based alcohols (ROH) and ethers [(ROR´), where R and R´ represent alkyl groups] are not possible structures for the formula C 4 H 8 O 2. There are not enough hydrogen atoms in the molecule for this to be the case.