Chapter 9 WITHIN SUBJECTS DESIGN 1 Within Between

Chapter 9 WITHIN- SUBJECTS DESIGN 1

Within & Between designs Within Subjects Students A B C D E Phonics 12 13 15 14 15 Whole Word 15 14 14 15 14 Between Subjects Students Phonics Whole Word A B C D E F G H I J 12 13 15 14 15 15 14 14 15 14 2 /29

repeated- measures A within- subjects experimental design, also known as a repeated- measures experimental design, compares two or more different treatment conditions ( or compares a treatment and a control) by observing or measuring the same group of individuals in all of the treatment conditions being compared. 3 /29

Advantages of Within- Subjects Designs 2 problems are reduced or eliminated in a within- subjects design. • • 1. Individual differences between groups can become a confounding variable. If the individuals in one treatment condition are noticeably different from the individuals in another treatment ( for example, smarter, faster, bigger, or older), the individual differences, rather than the treatments, may explain any observed differences. 2. The individual differences within each treatment condition can create high variance, which can obscure any differences between treatments. 4 /29

Examples 5 /29

Within subjects a within- subjects design is generally more powerful than a between- subjects design; that is, a within- subjects design is more likely to detect a treatment effect than a between- subjects design. 6 /29

Threats to internal validity for within- subjects designs 1 - Confounding from environmental variables (room difference, light difference, temperature difference) 7 /29

2 - Confounding from time- related factors. • • • History. Maturation. . Instrumentation. Testing effects. Statistical Regression 8 /29

3 - participant attrition Another potential problem for the within- subjects design is participant attrition. 9 /29

4 - Order Effects Carryover effect • Contrast effect (lighting in the cinema) • Progressive error • • Practice effect • Fatigue effect • Reduced motivation effect 10 /29

Dealing with time- related threats and order effects 11 /29

1 - Controlling Time • if the different treatment conditions are scheduled over a period of months, the chances greatly increase that an outside event ( history, maturation, or change in the measurement instrument) will have an influence on the results. • However if the time between treatments is too short other factors such as fatigue or reduced motivation may change the results 12 /29

2 - Switch to a Between- Subjects Design In some situations, order effects are so strong and so obvious that a researcher probably would not even consider using a within- subjects design. For example, a within-subjects design is a poor choice for a study comparing two methods of teaching reading to first- grade children. After the children have been taught with method I, they are permanently changed. 13 /29

3 - Counterbalancing The process of matching treatments with respect to time is called counterbalancing. 14 /29

Easy Case order effects evenly distributed between the treatment conditions it doesn’t matter which treatment comes first there is a constant (e. g. , d=5 points) change due to order effect 15 /29

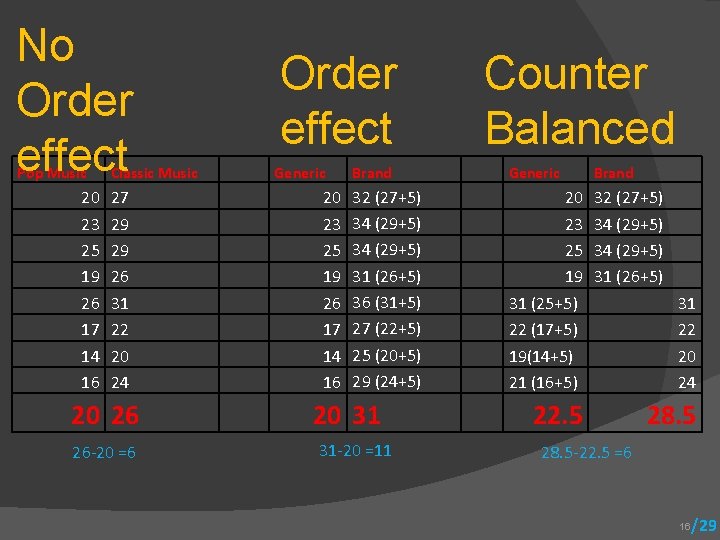
No Order effect Pop Music 20 23 25 19 26 17 14 16 Classic Music 27 29 29 26 31 22 20 24 20 26 26 -20 =6 Order effect Generic 20 23 25 19 26 17 14 16 Brand 32 (27+5) 34 (29+5) 31 (26+5) 36 (31+5) 27 (22+5) 25 (20+5) 29 (24+5) 20 31 31 -20 =11 Counter Balanced Generic Brand 20 23 25 19 31 (25+5) 22 (17+5) 19(14+5) 21 (16+5) 32 (27+5) 34 (29+5) 31 (26+5) 22. 5 31 22 20 24 28. 5 -22. 5 =6 16 /29

Limitations of Counterbalancing 17 /29

Limitation 1 • Counterbalancing balances the effect of ordering effect but it doesn’t eliminate it. So both means are inflated 18 /29

Limitation 2 A more serious problem is when counterbalancing adds order effect to some of the individuals but not to all. 19 /29

Limitation 3 When the order effect is not symmetrical One treatment might produce a larger order effect than the other treatment • Example? (Math & Statistics) • • In such situations, the order effects are not symmetrical, and counterbalancing the order of treatments does not balance the order effects. 20 /29

Limitation 4 Number of treatments With only two treatment conditions, complete counterbalancing is easy: There are only two possible sequences. However, as the number of treatments increases, complete counterbalancing becomes more complex. 21 /29

Number of Treatments 22 /29

Partial counter-balancing One solution to this problem is to use what is known as partial counterbalancing. A simple and unbiased procedure for selecting sequences is to construct a Latin square. 23 /29

Latin square 24 /29

Limitation of Latin square The Latin square is not a perfect example of partial counterbalancing because it does not balance every possible sequence of treatment conditions. For example, the first three groups all receive treatment A followed immediately by treatment B. 25 /29

Random order One method for improving the square is to use a random process to rearrange the columns ( for example, a coin toss to decide whether or not each column is moved) 26 /29

Statistical analyses With two treatment conditions, a repeated- measures t test For more than 2 treatments a single-factor ANOVA ( repeated measures) can be used to evaluate the statistical significance of the mean difference. 27 /29

Ordinal & nominal scale If the data are measured on an ordinal scale ( or can be rank ordered), a Wilcoxon test can be used to evaluate significant differences. If the data includes only positive and negative (nominal) effects then we use a sign test. 28 /29

Matched- Subjects Designs In a matched- subjects design, each individual in one group is matched with a participant in each of the other groups. The goal of a matched- subjects design is to duplicate all the advantages of within- and between- subjects designs without the disadvantages of either one. 29 /29