Chapter 9 Variable Selection and Model building RayBing

Chapter 9 Variable Selection and Model building Ray-Bing Chen Institute of Statistics National University of Kaohsiung 1

9. 1 Introduction 9. 1. 1 The Model-Building Problem • Ensure that the function form of the model is correct and that the underlying assumptions are not violated. • A pool of candidate regressors • Variable selection problem • Two conflicting objectives: – Include as many regressors as possible: the information content in these factors can influence the predicted values, y 2

– Include as few regressors as possible: the variance of the prediction increases as the number of the regressors increases • “Best” regression equation? ? ? • Several algorithms can be used for variable selection, but these procedures frequently specify different subsets of the candidate regressors as best. • An idealized setting: – The correct functional forms of regressors are known. – No outliers or influential observations 3

• • Residual analysis Iterative approach: 1. A variable selection strategy 2. Check the correct functional forms, outliers and influential observations • None of the variable selection procedures are guaranteed to produce the best regression equation for a given data set. 4

9. 1. 2 Consequences of Model Misspecification • The full model • The subset model 5

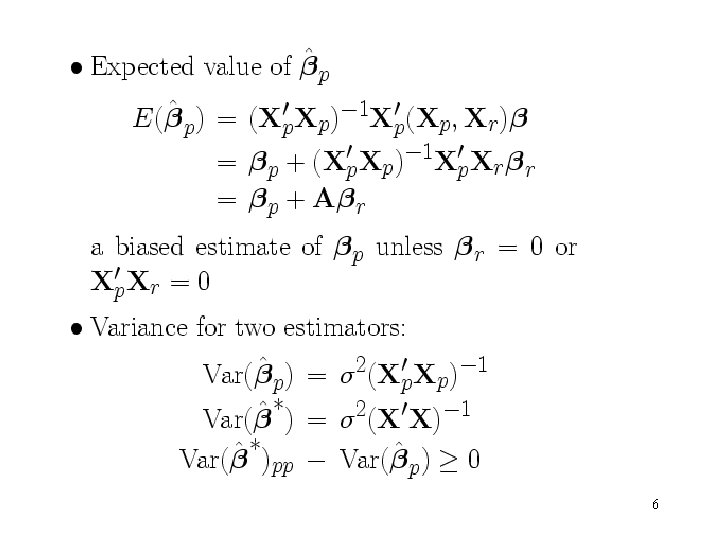
6

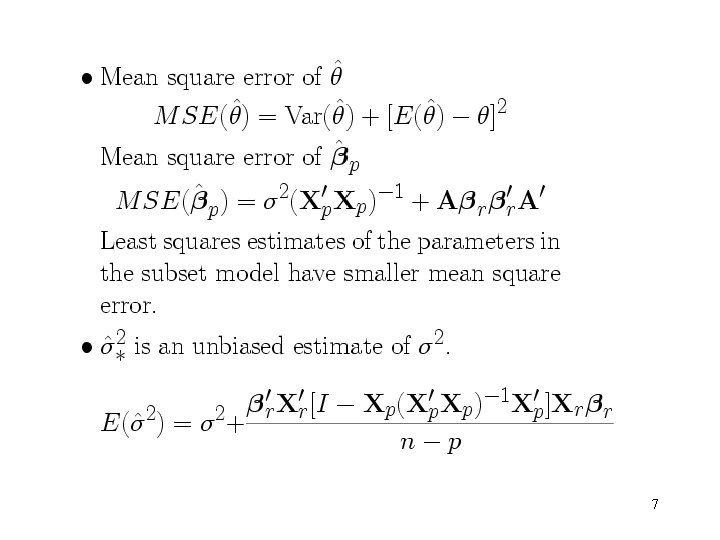
7

8

• Motivation for variable selection: – Deleting variables from the model can improve the precision of parameter estimates. This is also true for the variance of predicted response. – Deleting variable from the model will introduce the bias. – However, if the deleted variables have small effects, the MSE of the biased estimates will be less than the variance of the unbiased estimates. 9

9. 1. 3 Criteria for Evaluating Subset Regression Models • Coefficient of Multiple Determination: 10

– Aitkin (1974) : R 2 -adequate subset: the subset regressor variables produce R 2 > R 20 11

12

13

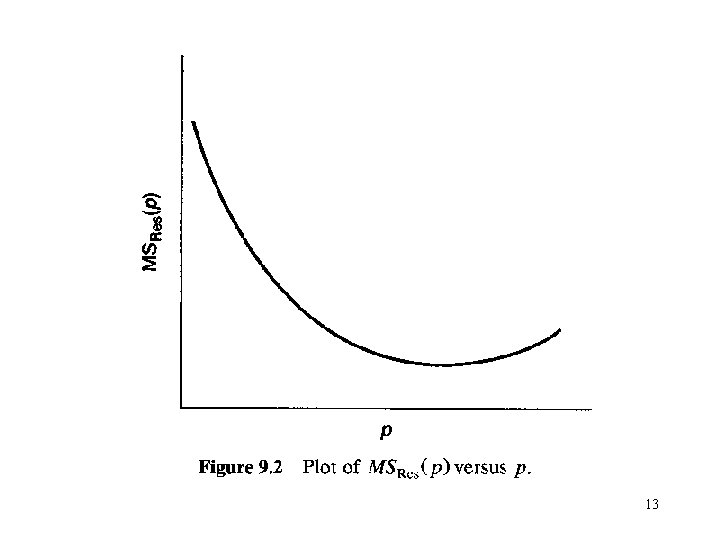
14

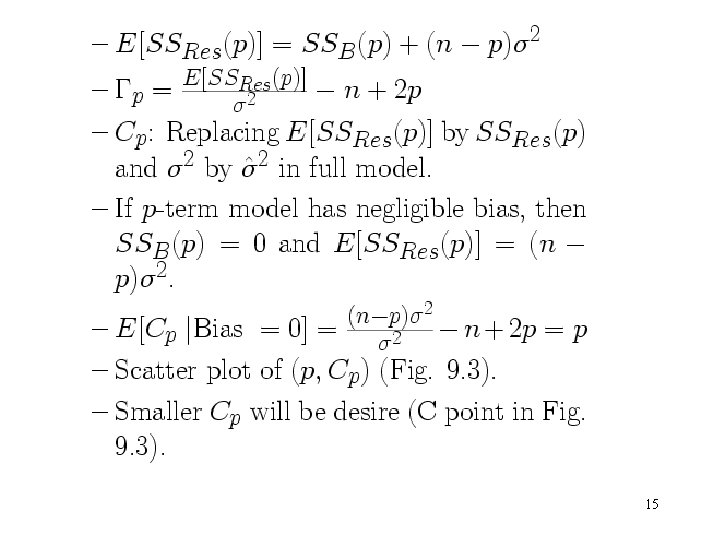
15

16

• Uses of Regression and Model Evaluation Criteria – Data description: Minimize SSRes and as few regressors as possible – Prediction and estimation: Minimize the mean square error of prediction. Use PRESS statistic – Parameter estimation: Chapter 10 – Control: minimize the standard errors of the regression coefficients. 17

9. 2 Computational Techniques for Variable Selection 9. 2. 1 All Possible Regressions • Fit all possible regression equations, and then select the best one by some suitable criterions. • Assume the model includes the intercept term • If there are K candidate regressors, there are 2 K total equations to be estimated and examined. 18

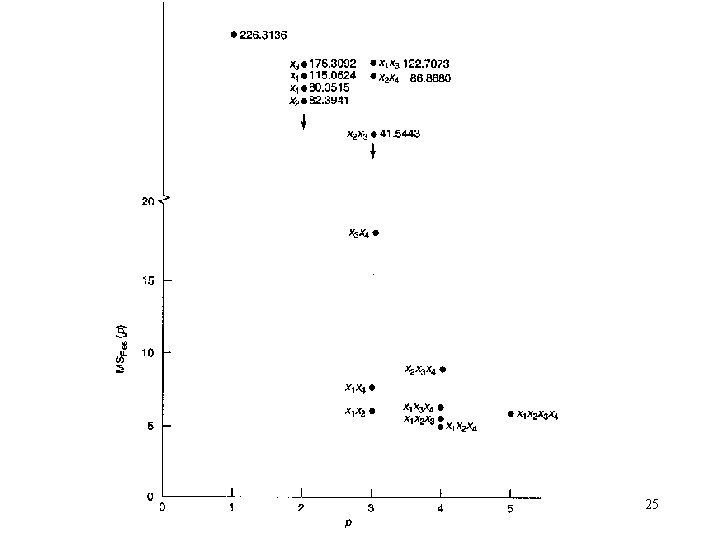
Example 9. 1 The Hald Cement Data 19

20

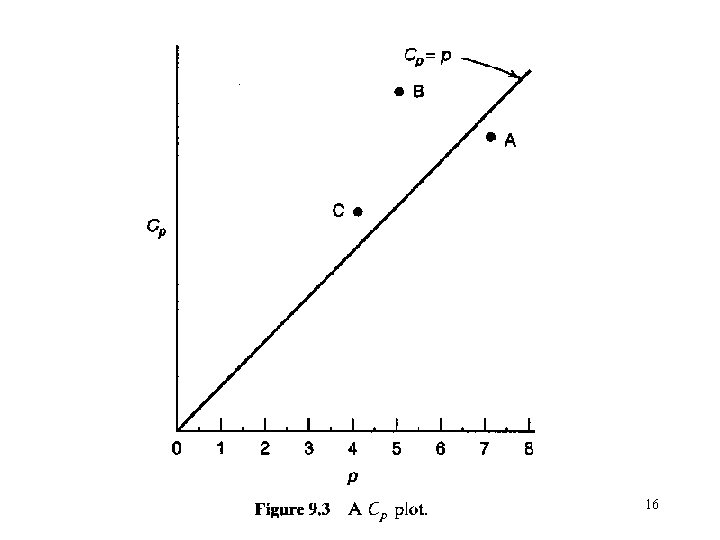
• R 2 p criterion: 21

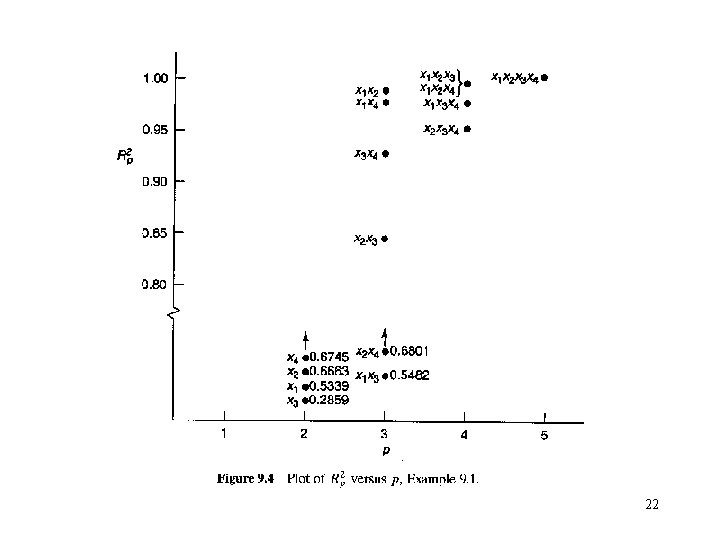
22

23

24

25

26

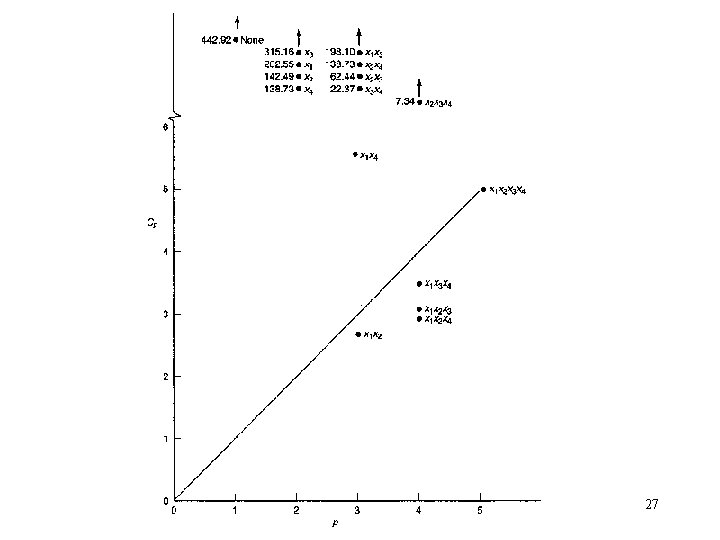
27

28

9. 2. 2 Stepwise Regression Methods • Three broad categories: 1. Forward selection 2. Backward elimination 3. Stepwise regression 29

30

Backward elimination – Start with a model with all K candidate regressors. – The partial F-statistic is computed for each regressor, and drop a regressor which has the smallest F-statistic and < FOUT. – Stop when all partial F-statistics > FOUT. 31

Stepwise Regression • A modification of forward selection. • A regressor added at an earlier step may be redundant. Hence this variable should be dropped from the model. • Two cutoff values: FOUT and FIN • Usually choose FIN > FOUT : more difficult to add a regressor than to delete one. 32