Chapter 9 System of Particles Center of Mass

Chapter 9, System of Particles Center of Mass Linear Momentum and Conservation Impulse Rocket

Center of Mass for a System of Particles The center of mass of a body or a system of bodies moves as though all of the mass were concentrated there and all external forces were applied there.

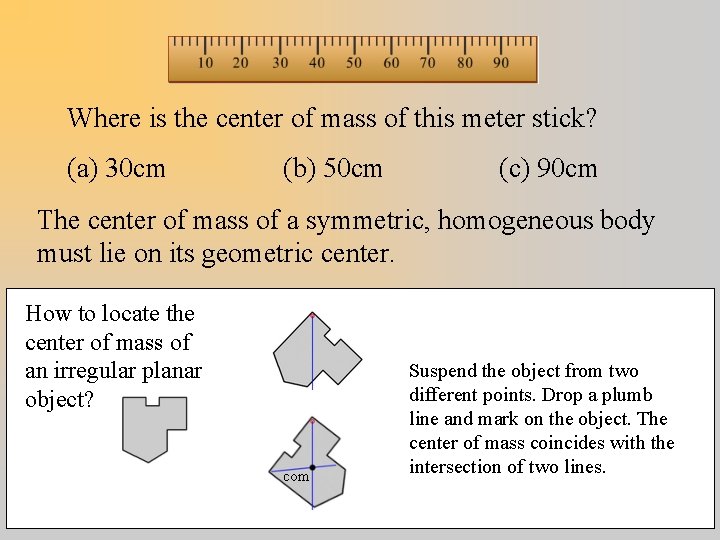
Where is the center of mass of this meter stick? (a) 30 cm (b) 50 cm (c) 90 cm The center of mass of a symmetric, homogeneous body must lie on its geometric center. How to locate the center of mass of an irregular planar object? com Suspend the object from two different points. Drop a plumb line and mark on the object. The center of mass coincides with the intersection of two lines.

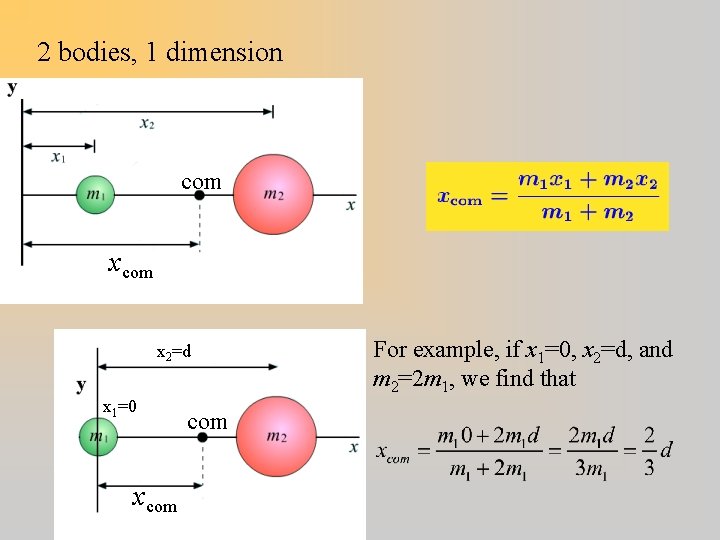
2 bodies, 1 dimension com x 2=d x 1=0 xcom For example, if x 1=0, x 2=d, and m 2=2 m 1, we find that

Example 1 X 1=0 X 2=d Earth Sun

Center of Mass for a System of Particles 2 particles, 1 dimension n particles, 3 dimensions, vector equation

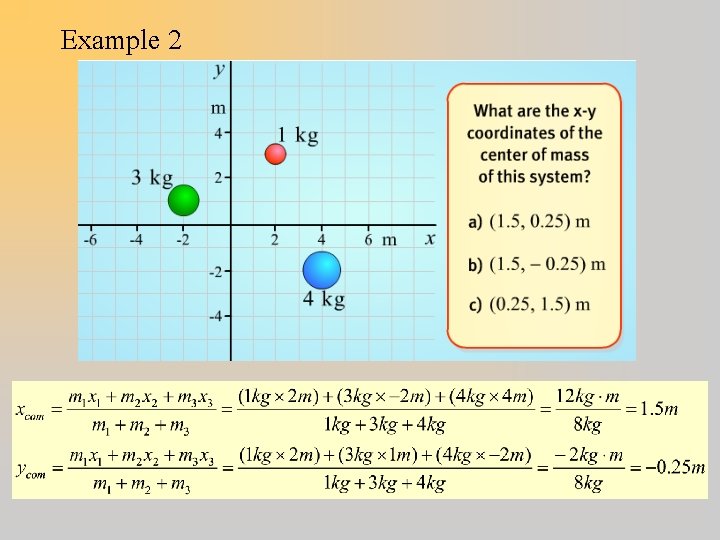
Example 2

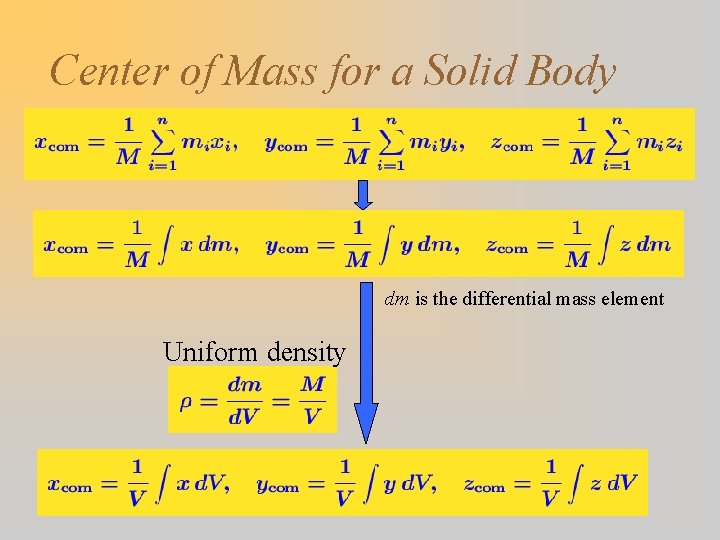
Center of Mass for a Solid Body dm is the differential mass element Uniform density

Newton’s 2 nd Law for a System of Particles particle system of particles The center of mass moves like an imaginary particle of mass M under the influence of the net external force on the system. A firework rocket explodes

Linear Momentum and Impulse Particle System

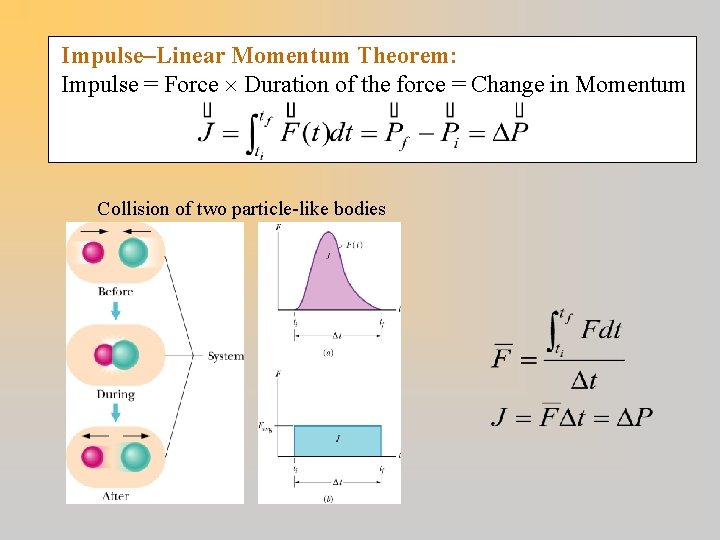
Impulse–Linear Momentum Theorem: Impulse = Force Duration of the force = Change in Momentum Collision of two particle-like bodies

Conservation of Linear Momentum If no net external force acts on a system of particles, the total linear momentum P of the system cannot change. If the component of the net external force on a closed system is zero along an axis, then the component of the linear momentum along that axis cannot change. ¬ Closed system (no mass enters or leaves) ¬ Isolated system (no external net force)

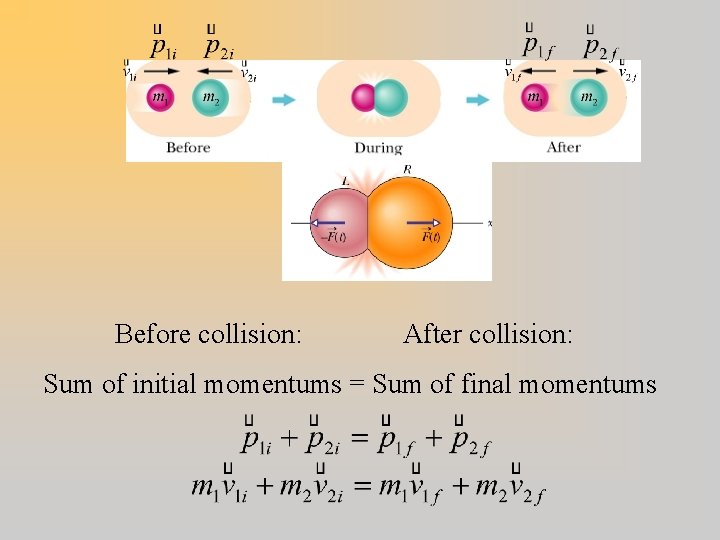
Before collision: After collision: Sum of initial momentums = Sum of final momentums

¬ ¬ Closed system (no mass enters or leaves) Isolated system (no external net force) Collisions in closed, isolated systems • Elastic • both colliding objects does not change their shapes • total linear momentum is conserved • total kinetic energy is conserved • Inelastic • the shape of one or both of object changes during the collision • total linear momentum is conserved • total kinetic energy is NOT conserved • Completely inelastic • the colliding objects stick together after the collision • total linear momentum is conserved • total kinetic energy is NOT conserved

In a closed, isolated system containing a collision, the linear momentum of each colliding body may change but the total momentum P of the system cannot change, whether the collision is elastic or inelastic.

Completely Inelastic Collisions in 1 D Velocity of Center of Mass

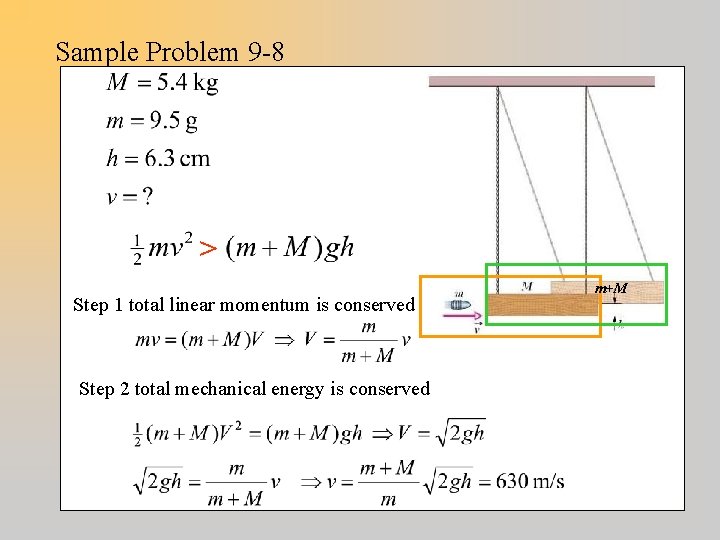
Sample Problem 9 -8 >? Step 1 total linear momentum is conserved Step 2 total mechanical energy is conserved m+M

Elastic Collisions in 1 D Equ. s (9 -67), (9 -68)

Sample Problem 9 -10 Step 1 Step 2

Rocket Propulsion A Rocket System (rocket + its ejected combustion products) is a closed, isolated system. The rocket is accelerated as a result of the thrust it receives from the ejected gases.

Rocket Equations First rocket equation: where R is the fuel consumption rate, vrel is the velocity of ejected fuel with respect to the rocket M is the instantaneous mass of the rocket a is the acceleration of the rocket T is referred to as the thrust of the rocket engine Second rocket equation: where vi and vf are initial and final velocities of the rocket Mi and Mf are the initial and final masses of the rocket

Summary #1 Center of mass: System of n particles Solid object with uniform density Newton’s second law: Linear momentum: Impulse-momentum theorem:

Summary #2 Conservation of momentum: Elastic collisions: Inelastic collisions: Completely inelastic collisions: Rocket equations: (closed, isolated system)