Chapter 9 Supplement Model Building 1 Introduction Regression

Chapter 9 Supplement Model Building 1

Introduction • Regression analysis is one of the most commonly used techniques in statistics. • It is considered powerful for several reasons: – It can cover a variety of mathematical models • linear relationships. • non - linear relationships. • nominal independent variables. – It provides efficient methods for model 2

Polynomial Models • There are models where the independent variables (xi) may appear as functions of a smaller number of predictor variables. • Polynomial models are one such example. 3

Polynomial Models with One Predictor Variable y = b 0 + b 1 x 1+ b 2 x 2 +…+ bpxp + e y = b 0 + b 1 x + b 2 x 2 + …+bpxp + e 4

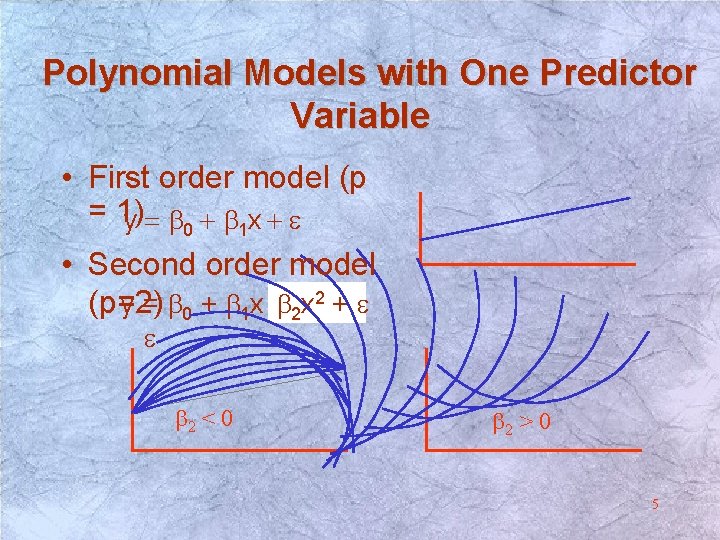
Polynomial Models with One Predictor Variable • First order model (p = 1) y = b 0 + b 1 x + e • Second order model y = b 0 + b 1 x b+2 x 2 + e (p=2) e b 2 < 0 b 2 > 0 5

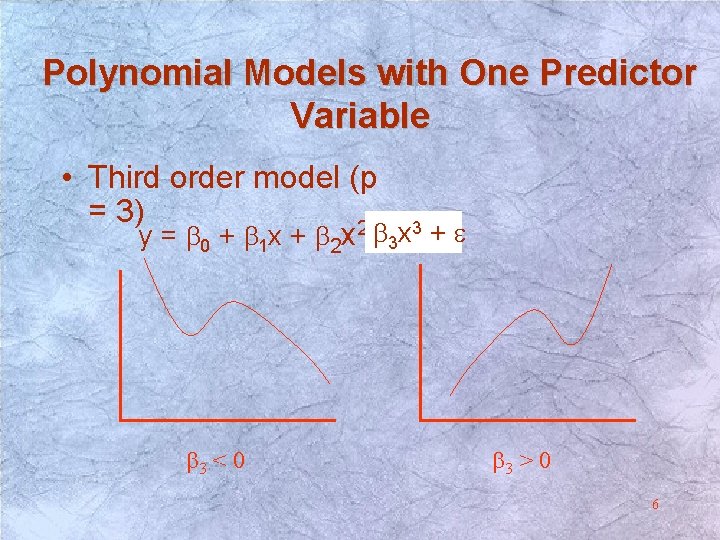
Polynomial Models with One Predictor Variable • Third order model (p = 3) y = b 0 + b 1 x + b 2 x 2 b+3 xe 3 + e b 3 < 0 b 3 > 0 6

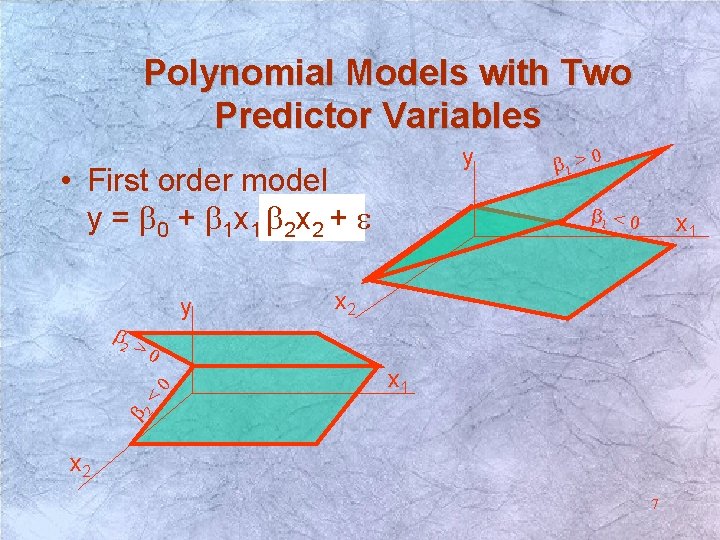
Polynomial Models with Two Predictor Variables y • First order model y = b 0 + b 1 x 1 b +2 ex 2 + e y b 1 < 0 x 1 x 2 >0 x 1 b 2 < 0 b 2 b 1 > 0 x 2 7

Polynomial Models with Two Predictor Variables • First order model y = b 0 + b 1 x 1 + b 2 x 2 + e The effect of one predictor variable on y is independent of the effect of the other predictor variable on y. +b 1 x 1 X 2 = 3 ] ) 3 ( [b 0+b 2 +b 1 x 1 X 2 = 2 ] ) 2 ( [b 0+b 2 ] +b 1 x 1 X = 1 2 (1) b 2 + [b 0 x 1 • First order model, two predictors, and interaction y = b 0 + b 1 x 1 + b 2 x 2 The two interact +bvariables x x + e 3 1 2 to affect the value of y. (3)]x 1 b + 3 b [ + 1 X 2 = 3 )] [b 0+b 2(3 [b 0+b 2(2)] +[b 1+b 3(2)]x 1 X 2 = 2 [b 0 +b ( 2 1)] +[b X =1 1 +b 3 (1)] x 1 2 x 8 1

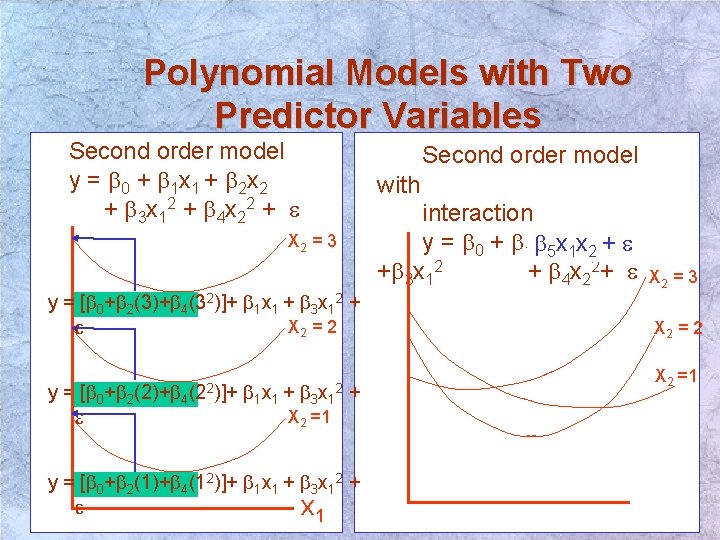
Polynomial Models with Two Predictor Variables Second order model y = b 0 + b 1 x 1 + b 2 x 2 + b 3 x 12 + b 4 x 22 + e Second order model with X 2 = 3 y = [b 0+b 2(3)+b 4(32)]+ b 1 x 1 + b 3 x 12 + X 2 = 2 e y = [b 0+b 2(2)+b 4 e (22)]+ b 1 x 1 + b 3 x 1 + 2 interaction y = b 0 + b 1 xb 15 x+1 xb 22 x+2 e +b 3 x 12 + b 4 x 22+ e X 2 = 3 X 2 = 2 X 2 =1 y = [b 0+b 2(1)+b 4(12)]+ b 1 x 1 + b 3 x 12 + e x 1 9

Selecting a Model • Several models have been introduced. • How do we select the right model? • Selecting a model: – Use your knowledge of the problem (variables involved and the nature of the relationship between them) to select a model. – Test the model using statistical techniques. 10

Selecting a Model; Example • Example: The location of a new restaurant – A fast food restaurant chain tries to identify new locations that are likely to be profitable. – The primary market for such restaurants is middle-income adults and their children (between the age 5 and 12). – Which regression model should be proposed to predict the profitability of new 11 locations?

Selecting a Model; Example • Solution – The dependent variable will be Gross Revenue – Quadratic relationships between Revenue and each predictor variable should be observed. Why? • Families with very young or older kids will not visit the restaurant as frequent as families with midrange ages of kids. • Members of middle-class families are more likely to visit a fast food restaurant than members of poor or wealthy families. Revenue Low Middle High Income Low Middle age High 12

Selecting a Model; Example • Solution – The quadratic regression model built is Sales = b 0 + b 1 INCOME + b 2 AGE + b 3 INCOME 2 +b 4 AGE 2 + b 5(INCOME)(AGE) +e Include interaction term when in doubt, and test its relevance later. SALES = annual gross sales INCOME = median annual household income in the neighborhood AGE = mean age of children in the neighborhood 13

Selecting a Model; Example To verify the validity of the proposed model for recommending the location of a new fast food restaurant, 25 areas with fast food restaurants were randomly selected. – Each area included one of the firm’s and three competing restaurants. – Data collected included (Xm 9 -01. xls): • Previous year’s annual gross sales. • Mean annual household income. • Mean age of children 14

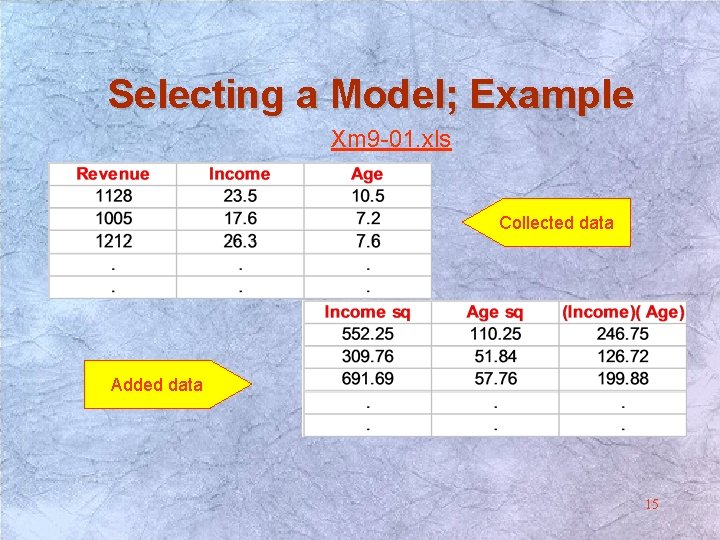
Selecting a Model; Example Xm 9 -01. xls Collected data Added data 15

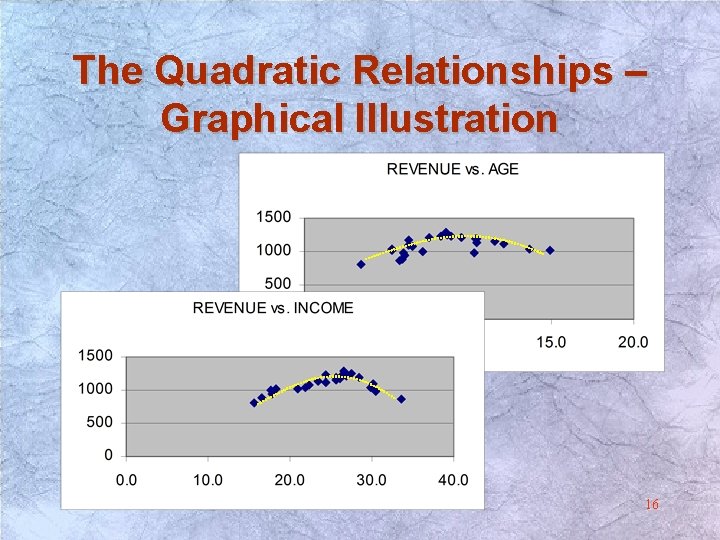
The Quadratic Relationships – Graphical Illustration 16

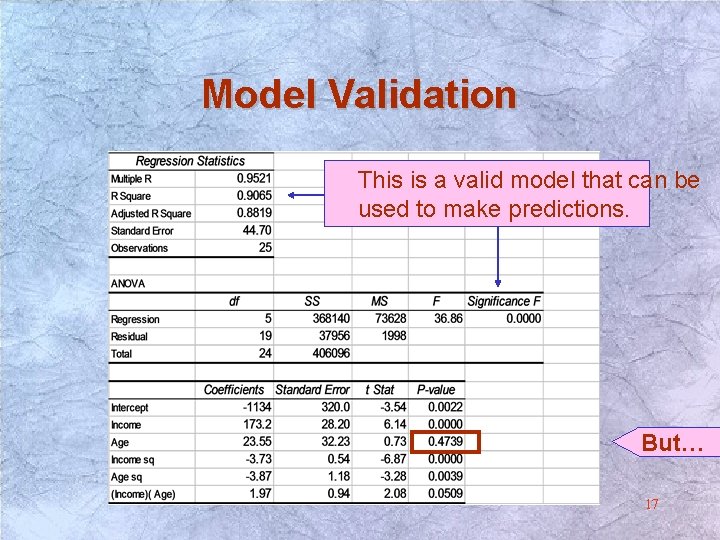
Model Validation This is a valid model that can be used to make predictions. But… 17

Reducing multicollinearity Model Validation The model can be used to make predictions …but multicollinearity is a problem!! The t-tests may be distorted, therefore, do not interpret the coefficients or test th In excel: Tools > Data Analysis > Correlation 18

Nominal Independent Variables • In many real-life situations one or more independent variables are nominal. • Including nominal variables in a regression analysis model is done via indicator variables. • An indicator variable (I) can assume one out of two values, “zero” orwas “one”. a degree earned is inbelow Finance 11 ifif the temperature 50 o 11 ifif adata firstwere condition collected out ofbefore two is 1980 met I= 00 ifif the o or asecond degree earned isout not Finance temperature was 50 more 00 ifif adata werecondition collected after ofin 1980 two is met 19

Nominal Independent Variables; Example: Auction Price of Cars A car dealer wants to predict the auction price of a car. Xm 9 -02 a_supp – The dealer believes now that odometer reading and the car color are variables that affect a car’s price. – Three color categories are considered: • White • Silver • Other colors Note: Color is a nominal variable. 20

Nominal Independent Variables; Example: Auction Price of Cars • data - revised (Xm 9 -02 b_supp) 1 if the color is white I 1 = 0 if the color is not white 1 if the color is silver I 2 = 0 if the color is not silver The category “Other colors” is defined by: I 1 = 0; I 2 = 0 21

How Many Indicator Variables? • Note: To represent the situation of three possible colors we need only two indicator variables. • Conclusion: To represent a nominal variable with m possible categories, we must create m-1 indicator variables. 22

Nominal Independent Variables; Example: Auction Car Price • Solution – the proposed model is y = b 0 + b 1(Odometer) + b 2 I 1 + b 3 I 2 + e – The data White car Other color Silver color 23

Example: Auction Car Price The Regression Equation From Excel we get the regression equation PRICE = 16701 -. 0555(Odometer)+90. 48(I-1)+295. For one additional mile the auction price decreases by A white car sells, on the average, 5. 55 cents. for $90. 48 more than a car of the “Other color” category A silver color car sells, on the averag for $295. 48 more than a car of the “Other color” category. 24

Example: Auction Car Price The Regression Equation From Excel (Xm 9 -02 b_supp) we get the regression equ PRICE = 16701 -. 0555(Odometer)+90. 48(I-1)+295. 48(IPrice The eq u silver c ation for a olor ca r. 16996. 48 -. 0 555(O domet Price = 16701 -. 0555(Odometer) + 90. 48(0) + 295 er) The eq u white c ation for a 16791 olor car. . 48 -. 0 555(O domet Price = 16701 -. 0555(Odometer) + 90. 48(1) + 295 16701 er) -. 0555 The equ (Odomete Price = 16701 -. 0555(Odometer) + 45. 2(0) + 148( ation fo r) r an “other c olor” ca r. Odometer 25

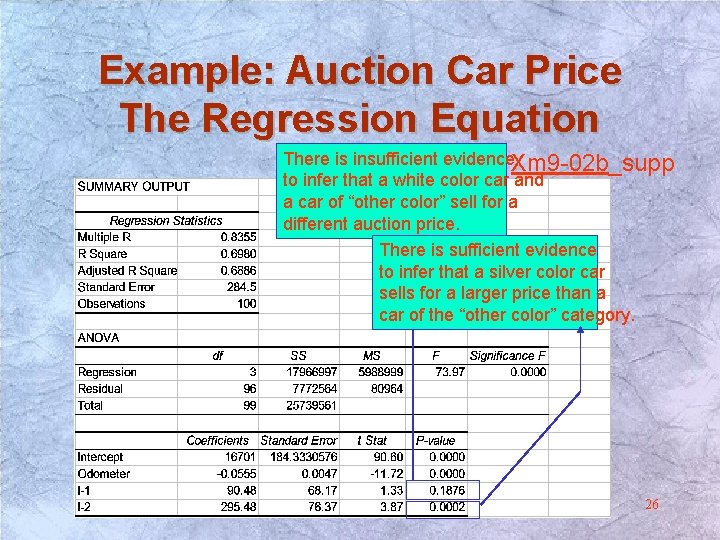
Example: Auction Car Price The Regression Equation There is insufficient evidence. Xm 9 -02 b_supp to infer that a white color car and a car of “other color” sell for a different auction price. There is sufficient evidence to infer that a silver color car sells for a larger price than a car of the “other color” category. 26

Nominal Independent Variables; Example: MBA Program Admission (MBA II) • The Dean wants to evaluate applications for the MBA program by predicting future performance of the applicants. • The following three predictors were suggested: – Undergraduate GPA Note: The undergraduate – GMAT score degree is nominal data. – Years of work experience • It is now believed that the type of undergraduate degree should be included in the model. 27

Nominal Independent Variables; Example: MBA Program Admission 1 if B. A. I 1 = 0 otherwise 1 if B. B. A I 2 = 0 otherwise 1 if B. Sc. or B. Eng. I 3 = 0 otherwise The category “Other group” is defined by: I 1 = 0; I 2 = 0; I 3 = 0 28

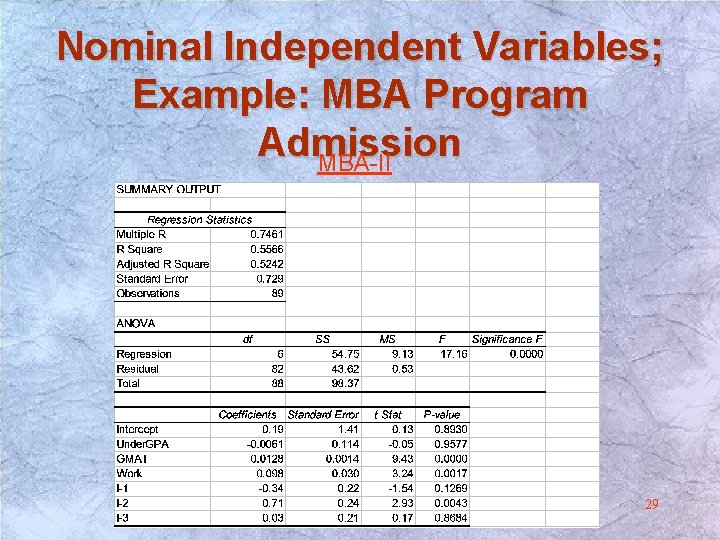
Nominal Independent Variables; Example: MBA Program Admission MBA-II 29

Applications in Human Resources Management: Pay. Equity • Pay-equity can be handled in two different forms: – Equal pay for equal work – Equal pay for work of equal value. • Regression analysis is extensively employed in cases of equal pay for equal work. 30

Human Resources Management: Pay-Equity • Example (Xm 9 -03_supp) – Is there sex discrimination against female managers in a large firm? – A random sample of 100 managers was selected and data were collected as follows: • • Annual salary Years of education Years of experience Gender 31

Human Resources Management: Pay-Equity • Solution – Construct the following multiple regression model: y = b 0 + b 1 Education + b 2 Experience + b 3 Gender + e – Note the nature of the variables: • Education – Interval • Experience – Interval • Gender – Nominal (Gender = 1 if male; =0 otherwise). 32

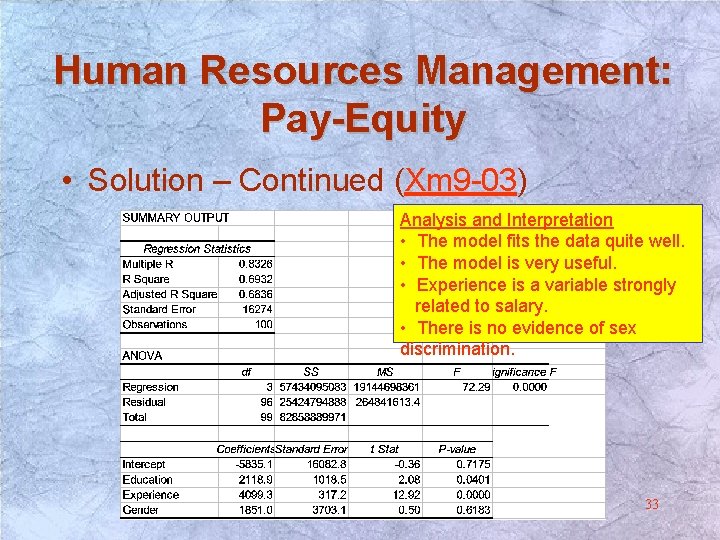
Human Resources Management: Pay-Equity • Solution – Continued (Xm 9 -03) Analysis and Interpretation • The model fits the data quite well. • The model is very useful. • Experience is a variable strongly related to salary. • There is no evidence of sex discrimination. 33

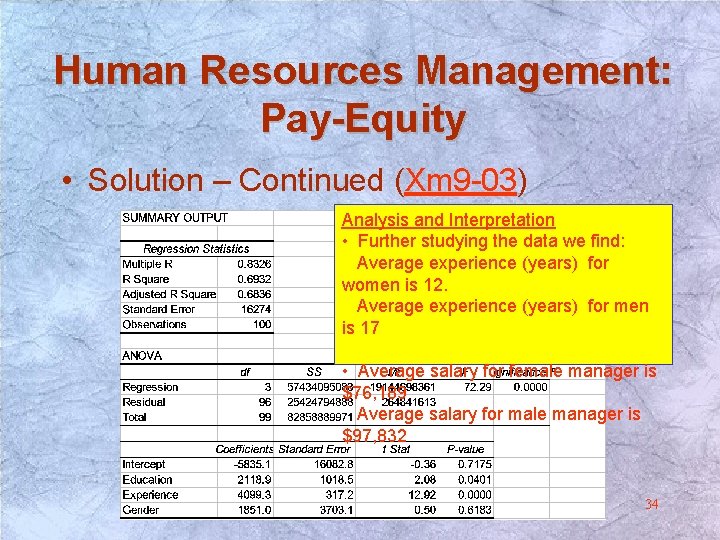
Human Resources Management: Pay-Equity • Solution – Continued (Xm 9 -03) Analysis and Interpretation • Further studying the data we find: Average experience (years) for women is 12. Average experience (years) for men is 17 • Average salary for female manager is $76, 189 Average salary for male manager is $97, 832 34

Stepwise Regression • Multicollinearity may prevent the study of the relationship between dependent and independent variables. • The correlation matrix may fail to detect multicollinearity because variables may relate to one another in various ways. • To reduce multicollinearity we can use stepwise regression. • In stepwise regression variables are added to or deleted from the model one at a time, based on their contribution to the current 35 model.

Model Building • Identify the dependent variable, and clearly define it. • List potential predictors. – Bear in mind the problem of multicollinearity. – Consider the cost of gathering, processing and storing data. – Be selective in your choice (try to use as few variables as possible). 36

• Gather the required observations (have at least six observations for each • independent Identify several possible models. variable). – A scatter diagram of the dependent variables can be helpful in formulating the right model. – If you are uncertain, start with first order and second order models, with and without interaction. – Try other relationships (transformations) if the polynomial models fail to provide a good fit. • Use statistical software to estimate the 37

• Determine whether the required conditions are satisfied. If not, attempt to correct the problem. • Select the best model. – Use the statistical output. – Use your judgment!! 38