Chapter 9 Stoichiometry Stoichiometry l Stoichiometry is probably
Chapter 9: Stoichiometry

Stoichiometry l Stoichiometry is probably the most important concept of all of chemistry. l l l Is the calculation of quantities in chemical equations. We’ve done a bit of it in chapter 7, but now we do more May want to refresh chapter 7 before we get too far into this

9. 1 Interpreting Chemical Equations Any given equation will give us a wealth of information. l We will use the equation N 2(g) + 3 H 2(g) 2 NH 3(g) to study this. l We must ask, what kind of information can we gain from this equation? l

N 2(g) + 3 H 2(g) 2 NH 3(g) Particles/Moles 1. l 1 mol nitrogen to 3 moles hydrogen = 2 moles ammonia l N and H will always react to form ammonia in this 1: 3: 2 ratio l If we have 20 moles of N, how many moles of H needed to maintain this ratio? § § How many moles of ammonia would this form? l § l 60 moles H needed Can do this from a unit conversion 40 moles ammonia So, given the quantity of one chemical, we can find the quantity needed for another.

N 2(g) + 3 H 2(g) 2 NH 3(g) Mass 2. l l Knowing the number of moles of a chemical lets me find its mass. How? l Molar mass of the substance If I needed 60 moles of H 2, what mass of H 2 would I need? So, knowing balanced equation can let us find how much mass is involved in the reaction.

N 2(g) + 3 H 2(g) 2 NH 3(g) 3. Volume l l l If we assume STP, this equation can also give me information regarding the volume of these gases Remember 1 mole of gas at STP = 22. 4 L So if I had 20 moles of N 2 gas, how many liters of H 2 gas will I need? l l l Remember, for every mole of N 2 gas, 3 moles of H 2 gas. So 20 moles N 2 gas = 60 moles of H 2 gas Through mole volume conversion, 1344 L H 2 gas

Overview of this l l l It all comes down to the mole ratios between each of the substances involved in the reaction. We MUST remember the mole ratios. Luckily, if our equation is balanced, the ratios are written right there for us! H 2(g) + I 2(g) 2 HI(g) Ratio of 1 mol H 2: 1 mol I 2: 2 mol HI Or 1: 1: 2 l How do I know this?

9. 2 - Mole Conversions (aka Chemical Calculations) l l l All starts with a balanced equation. N 2(g) + 3 H 2(g) 2 NH 3(g) I want to know how many moles of ammonia (NH 3) are produced when. 6 mol of N 2 react with hydrogen. To do this, I will use the mole ratios given by the balanced equation. I know that for every 1 mole of N 2, I will need 2 moles of NH 3 This gives me ratios which can be used in unit conversions.

N 2(g) + 3 H 2(g) 2 NH 3(g) l Just do the unit conversion l The equation has just given us another conversion we can use. Lets try this one… How many moles of nitrogen will it take to produce 7. 24 moles of ammonia? l l

N 2(g) + 3 H 2(g) 2 NH 3(g) l Similar conversion

Mass Calculations l l Just like we can go from mole using a balanced equation, we can also go from mass. You still need the balanced equation And like the moles, must pay attention to the mole ratio of all of the substances in the equation. But also must use molar mass

Example N 2(g) + 3 H 2(g) 2 NH 3(g) l l Same equation as before. Might as well stick with it. We want to find number of grams produced by the reaction of 5. 4 g hydrogen with an excess of nitrogen l l The statement, “…excess of nitrogen” is important. It means we don’t have to worry about how much N 2 we have, and can focus just on the amount of H 2

N 2(g) + 3 H 2(g) 2 NH 3(g) l l l Every relationship between chemicals in an equation is held together by the mole ratios. We must use those same ratios now. Path to follow l l l Mass of hydrogen mol ammonia mass ammonia Notice, had to go to moles to link between different substances. ALWAYS must use mole ratios to convert between substances

N 2(g) + 3 H 2(g) 2 NH 3(g)

Waste of space? l l l That took up a whole slide. Did it need to? No. Could have done it all as one, long conversion.

l l We put in 5. 4 g H 2 and got out 31 g NH 3 Did this violate the conservation of mass?

Other Stoichiometric Calculations l From a balanced equation you get the mole ratios l l From mole ratios, you can find any unit of measurement related to the mole l Volume, particles, mass Once you have the mole ratio, you can convert between any of these items freely l Mass-volume, volume-volume, mass-particle, particlevolume, etc. But the first step with ANY of these problems, is to convert what you are given into moles. However, most common stoichiometry problem is mass.

Volume-Volume Example l l l Assuming STP, how many liters of O 2 are needed to produce 19. 8 L SO 3? 2 SO 2(g) + O 2(g) 2 SO 3 Need a path from liters of one substance to liters of another. MUST use mole conversion Write down a path you think would work L SO 3 mol O 2 L O 2
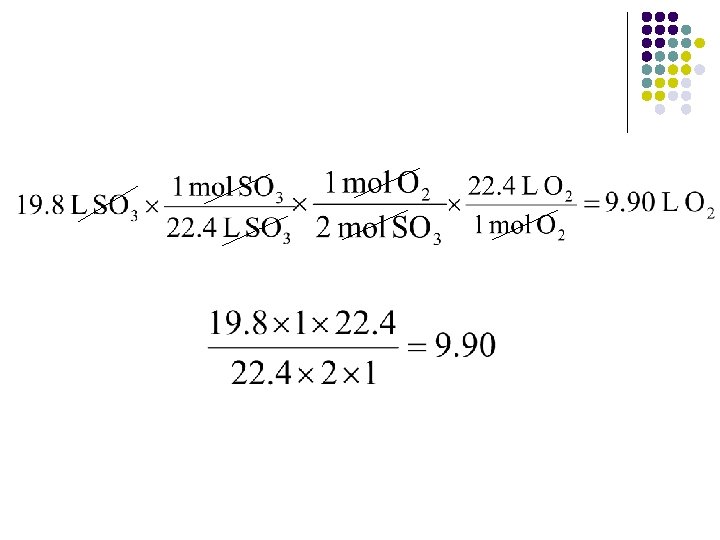

9. 3 Limiting Reagent and Percent Yield l l l Also known as limiting reactant problems The limiting reagent in a reaction is what limits how much product can be produced. In other words, it is impossible to make a certain amount of a desired compound if there is not enough of all the reactants.

N 2(g) + 3 H 2(g) 2 NH 3 l Yes, the return of the ammonia reaction! l l l Hahaha!!!! What this says, is that for this reaction to occur, I need 1 molecule of N 2 to react with 3 molecules of H 2, and then I will produce 2 molecules of NH 3 What would happen if 2 molecules of N 2 tried to react with 3 molecules of H 2? Would more than 2 molecules of NH 3 be produced? In this case, H 2 would be the limiting reagent, since it is what is determining how much product I can have. But N 2 would be the excess reagent, since there is more than enough of it to react with the limiting reagent.

How to Determine Limiting Reagent Note: This process can be long. Let’s use 2 Na(s) + Cl 2(g) 2 Na. Cl(s) as an example What will happen when I react 6. 70 moles of Na with 3. 20 moles of Cl 2? Three things I want to know l l 1. 2. 3. What is the limiting reagent? How many moles of Na. Cl are produced? How much of the excess reagent remains unreacted?

What is the limiting reagent? l l l Start with one of the known quantities of reactants. Doesn’t matter which. Use the mole ratio to calculate how much of the other reactant is needed. I’ll start with Cl 2 So, according to our amount of Cl 2, we need at least 6. 40 moles of Na If we have more Na than our calculated amount needed, Cl 2 is our limiting reagent. If we have less than the calculated amount needed, Na is our limiting reagent.

To double-check l Same rules apply, but lets look at Na. l Again, what this shows, is from the amount of Na that we have, we’d need 3. 35 moles of Cl 2 to fully react. If we have more Cl 2 than our calculated needed amount, Na is the limiting reagent. If we have less Cl 2 than our calculated amount, then Cl 2 is the limiting reagent. l

l So no matter which method we use, both show that Cl 2 is our limiting reagent l l l Since Na shows we need 3. 35 moles of Cl 2 to react fully (we only have 3. 20 moles) Also, since Cl 2 shows we only need 6. 40 moles of Na to react fully with it (but we have 6. 70 moles) This is how you determine a limiting reagent.

Steps for Limiting Reagent 1. 2. 3. 4. Pick a reactant to start with. Doesn’t matter which one. Using mole ratios, calculate how much of the other reactant is needed to react fully with the one we have chosen. If we have more of the other than the calculated amount, the one we have chosen is the limiting reagent. If we have less of the other than the calculated amount, the other is the limiting reagent.

How many moles of Na. Cl will be produced? l l l Now that we know what the limiting reagent is, we will use that one to determine how much product we have. Remember, Cl 2 is the limiting reagent. So, with only 3. 20 mol Cl 2, we can generate 6. 4 mol Na. Cl.

How much of the excess reagent remains unreacted? l The amount of the excess is the amount of the excess reagent we started with minus the amount of excess reagent we used. Must first determine how much excess reagent we used. To the mole ratios! l 6. 70 mole – 6. 4 mole = 0. 30 mole unreacted! l l

When there are no moles… l l l Probably because of trapping Sometimes you’re not given your initial quantities in moles, you’re given them in grams, or liters. When this occurs, you must first convert your grams into moles before you begin your limiting reagent calculation.
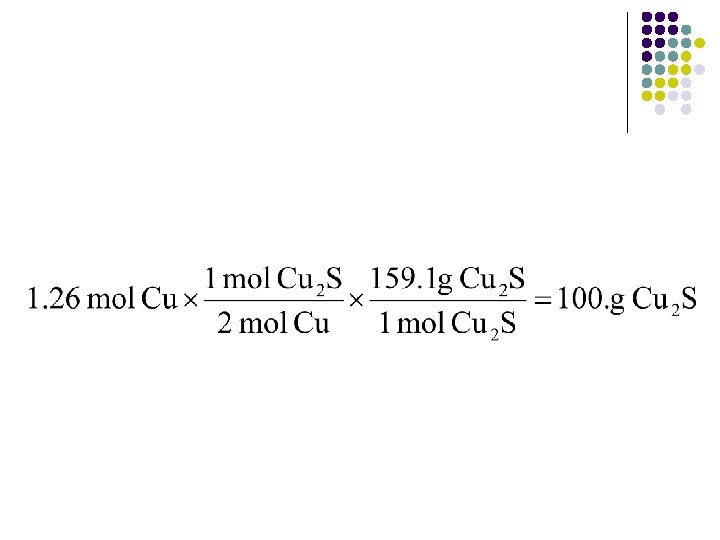
Example l l l 2 Cu(s) + S(s) Cu 2 S(s) What is the maximum number of grams of Cu 2 S that can be formed when 80. 0 g of Cu react with 25. 0 g of S? First, find # of moles of each. l 1. 26 moles Cu; 0. 779 mol S

l l Now, pick either Cu or S, your choice. Made your decision? Now determine how many moles of the other reactant you would need. Which is the limiting reagent? l l Copper! Now that we know copper is the limiting reagent, we can proceed with our calculation of mass of Cu 2 S.

Percent Yield l Oftentimes, the amount of product we actually get is less than the expected amount of product. l l When using stoichiometry, we’ve been calculating theoretical yield. l l Might have had incorrect measurements, impure samples, competing side reactions, loss of sample during measurement, etc. This is the ideal, maximum amount of product that, according to stoichiometric calculations, should be produced. Contrasted with the actual yield l l l Which is the actual amount of product produced. Found through experimental data Often less than theoretical yield

Percent Yield l The percent yield is the ratio of the actual to theoretical yield, expressed as a percentage. l Since actual should be less than theoretical, percent yield should not be more than 100%.

Example Calculation l l Calcium carbonate decomposes by heating Ca. CO 3(s) Ca. O(s) + CO 2(g) What is the percent yield of this reaction if 24. 8 g of Ca. CO 3 is heated to give 13. 1 g of Ca. O? The problem tells us the actual yield is 13. 1 g. Need to use stoichiometry to determine theoretical yield.
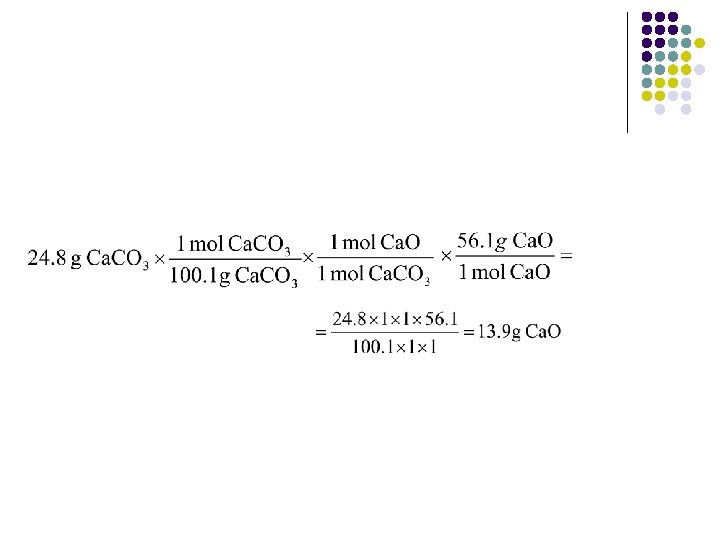

l l So theoretical yield is 13. 9 g Ca. O Now we can find the percent yield.
- Slides: 37