Chapter 9 Sampling Distributions 1 9 1 Introduction

Chapter 9 Sampling Distributions 1

9. 1 Introduction w In real life, calculating parameters of populations is prohibitive because populations are very large. w Rather than investigating the whole population, we take a sample, calculate a statistic related to the parameter of interest, and make an inference. w The sampling distribution of the statistic is the tool that tells us how close is the statistic to the parameter. Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 2

9. 2 Sampling Distribution of the Mean w An example n n A die is thrown infinitely many times. Let X represent the number of spots showing on any throw. The probability distribution of X is x p(x) 1 2 1/6 3 4 5 1/6 1/6 E(X) = 1(1/6) + 2(1/6) + 3(1/6)+ 6 …………………. = 3. 5 1/6 V(X) = (1 -3. 5)2(1/6) + (2 -3. 5)2(1/6) + …………. …= 2. 92 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 3

Throwing a die twice – sample mean w Suppose we want to estimate m from the mean of a sample of size n = 2. w What is the distribution of ? Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 4

Throwing a die twice – sample mean Copyright © 2005 Brooks/Cole, a division of

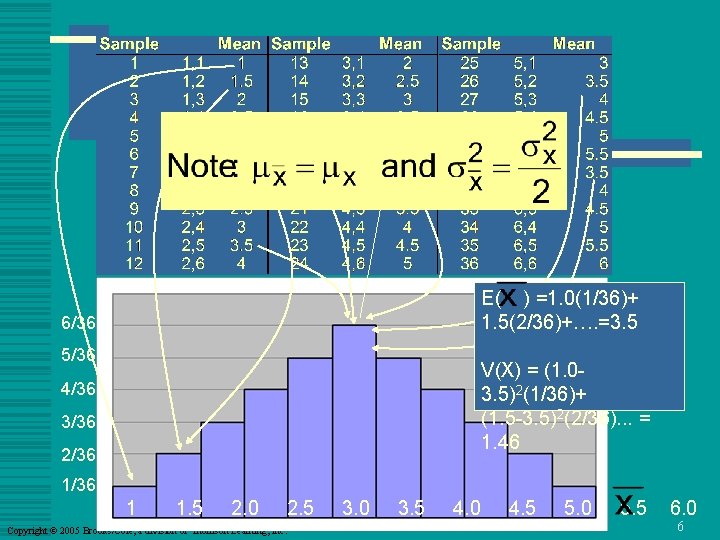
The distribution of when n = 2 E( ) =1. 0(1/36)+ 1. 5(2/36)+…. =3. 5 6/36 5/36 V(X) = (1. 03. 5)2(1/36)+ (1. 5 -3. 5)2(2/36). . . = 1. 46 4/36 3/36 2/36 1 1. 5 2. 0 2. 5 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 3. 0 3. 5 4. 0 4. 5 5. 0 5. 5 6. 0 6

Sampling Distribution of the Mean 6 Copyright © 2005 Brooks/Cole, a division of Thomson

Sampling Distribution of the Mean Notice that is smaller than sx. The larger the sample size the smaller. Therefore, tends to fall closer to m, as the sample size increases. Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 8

Generalized Mean and Variance w We can generalize the mean and variance of the sampling of two dice to n dices. w The standard deviation of the sampling distribution is called ‘the standard error’. Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 9

The Central Limit Theorem w If a random sample is drawn from any population, the sampling distribution of the sample mean is approximately normal for a sufficiently large sample size. w The larger the sample size, the more closely the sampling distribution of will resemble a normal distribution. Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 10

Sampling Distribution of the Sample Mean § If the population is normal, then n. is normally distributed for all values of § If the population is non-normal, then larger values of n. is approximately normal only for § In most practical situations, a sample size of 30 may be sufficiently large to allow us to use the normal distribution as an approximation for the sampling distribution of. Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 11

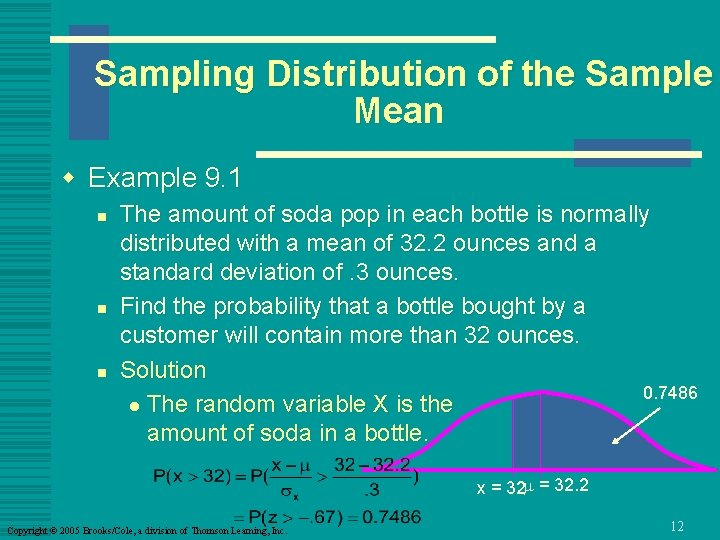
Sampling Distribution of the Sample Mean w Example 9. 1 n n n The amount of soda pop in each bottle is normally distributed with a mean of 32. 2 ounces and a standard deviation of. 3 ounces. Find the probability that a bottle bought by a customer will contain more than 32 ounces. Solution 0. 7486 l The random variable X is the amount of soda in a bottle. x = 32 m = 32. 2 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 12

Sampling Distribution of the Sample Mean w Find the probability that a carton of four bottles will have a mean of more than 32 ounces of soda per bottle. w Solution n Define the random variable as the mean amount of soda per bottle. 0. 9082 0. 7486 x = 32 m = 32. 2 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 13

Sampling Distribution of the Sample Mean w Example 9. 2 n n n Dean’s claim: The average weekly income of B. B. A graduates one year after graduation is $600. Suppose the distribution of weekly income has a standard deviation of $100. What is the probability that 36 randomly selected graduates have an average weekly income of less than $550? Solution (By central limit theorem, follows normal distribution. Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 14

Sampling Distribution of the Sample Mean w Example 9. 2– continued n n If a random sample of 36 graduates actually had an average weekly income of less than $550, what would you conclude about the validity of the claim that the average weekly income is 600? Guess l l With m = 600 the probability of observing a sample mean as low as 550 is very small (0. 0013). The claim that the mean weekly income is $600 is probably unjustified. It will be more reasonable to assume that m is smaller than $600, because a sample mean of less than $550 becomes more probable. Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 15

Using Sampling Distributions for Inference w What would be the reasonable sample mean if we know about population parameters? w Sampling distribution provides reasonable inference about the sample mean. - Z. 025 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 16

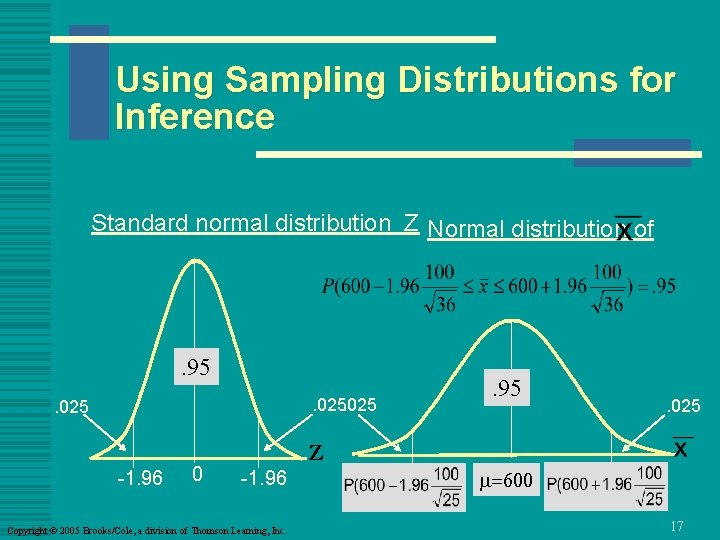
Using Sampling Distributions for Inference Standard normal distribution Z Normal distribution of . 95. 025 -1. 96 0 Z -1. 96 Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. . 95 . 025 m m=600 17

Using Sampling Distributions for Inference w Conclusion n n There is 95% chance that the sample mean falls within the interval [567. 3, 632. 7] if the population mean is really 600. Suppose that the sample mean is 550. If the population mean of 600 is claimed by somebody but his or her claim is not sure. l The sample mean of 550 is too small to justify μ =600. Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 18

Sampling Distribution: Difference of two means The final sampling distribution introduced is that of the difference between two sample means. This requires: è independent random samples be drawn from each of two normal populations If this condition is met, then the sampling distribution of the difference between the two sample means, i. e. will be normally distributed. (note: if the two populations are not both normally distributed, but the sample sizes are “large” (>30), the distribution of is approximately normal) Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 9. 19

Sampling Distribution: Difference of two means The expected value and variance of the sampling distribution of are given by: mean: standard deviation: (also called the standard error if the difference between two means) Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 9. 20

Example 9. 3… § Since the distribution of is normal and has a mean of and a standard deviation of § We can compute Z (standard normal random variable) in this way: Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 9. 21

Example 9. 3… § Starting salaries for MBA grads at two universities are normally distributed with the following means and standard deviations. Samples from each school are taken… University 1 University 2 Mean 62, 000 $/yr 60, 000 $/yr Std. Dev. 14, 500 $/yr 18, 300 $/yr 50 60 sample size n § What is the probability that the sample mean starting salary of University #1 graduates will exceed that of the #2 grads? Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 9. 22

Example 9. 3… § “What is the probability that the sample mean starting salary of University #1 graduates will exceed that of the #2 grads? ” § We are interested in P(X 1 > X 2). Converting this to a difference of means, what is: P(X 1 – X 2 > 0) ? Z § “there is about a 74% chance that the sample mean starting salary of U. #1 grads will exceed that of U. #2” Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 9. 23

From Here to Inference § In Chapters 7 and 8 we introduced probability distributions, which allowed us to make probability statements about values of the random variable. § A prerequisite of this calculation is knowledge of the distribution and the relevant parameters. Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 9. 24

From Here to Inference § The knowledge of the population distribution and its parameter(s) allows us to use the probability distribution to make probability statements about individual members (sample) of the population. Population Distribution and Parameters Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. Probability of Individual Sample 9. 25

From Here to Inference § In this chapter we developed the sampling distribution, wherein knowledge of the parameter(s) and some information about the distribution allow us to make probability statements about a sample statistic. Central Limit Parameters , Theorem § Sample Distribution Known or Unknown and Probability of Population Distribution Sample Statistic Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 9. 26

From Here to Inference § Starting in Chapter 10, we will assume that most population parameters are unknown. § The statistics practitioner will sample from the population and compute the required statistic. § The sampling distribution of that statistic will enable us to draw inferences about the parameter. Although we do not have information about the population distribution, we still use the normal distribution as the sample distribution of the sample mean because of the central limit theorem. § Copyright © 2005 Brooks/Cole, a division of Thomson Learning, Inc. 9. 27