Chapter 9 Rotation of rigid bodies Radian Vs

Chapter 9 Rotation of rigid bodies

Radian Vs Degree

Using Radian

Example

Example What is θ in radians and in degrees?
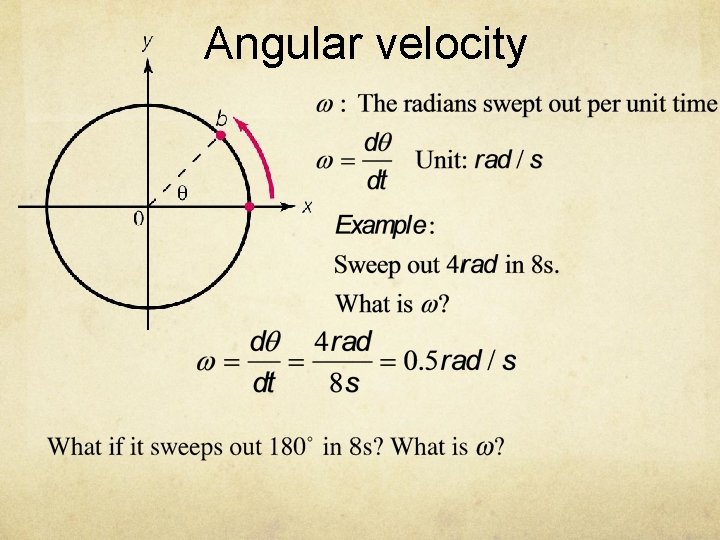
Angular velocity
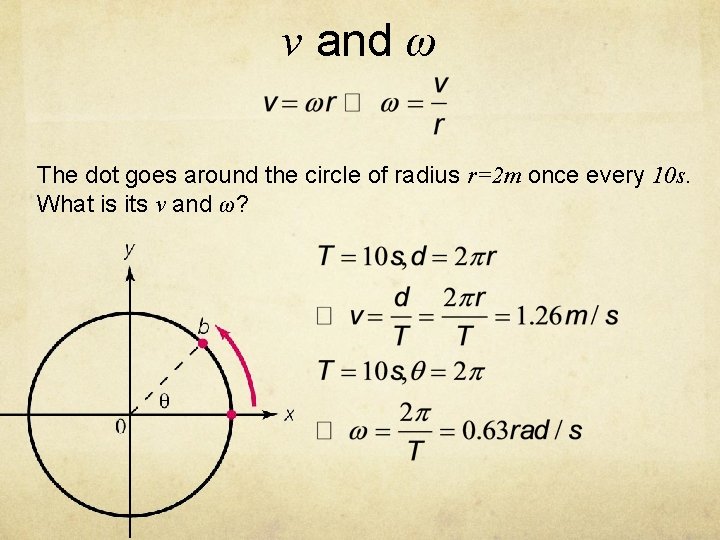
v and ω The dot goes around the circle of radius r=2 m once every 10 s. What is its v and ω?

Meaning of different variables

Must remember this: Using this you can convert freely among ω, T, f and v.

Period T and frequency f

Example Given r =2 m, T=10 s, find v and ω.

Example Given r =2 m, f = 20 rpm, find v and ω.

Example A car takes 5 minutes to complete one circle on the race track. What is its angular velocity?

Equations of Circular Motion (Must Memorize) y v (x, y) r x

Units

Angular acceleration α

Equations of Motion Linear Circular
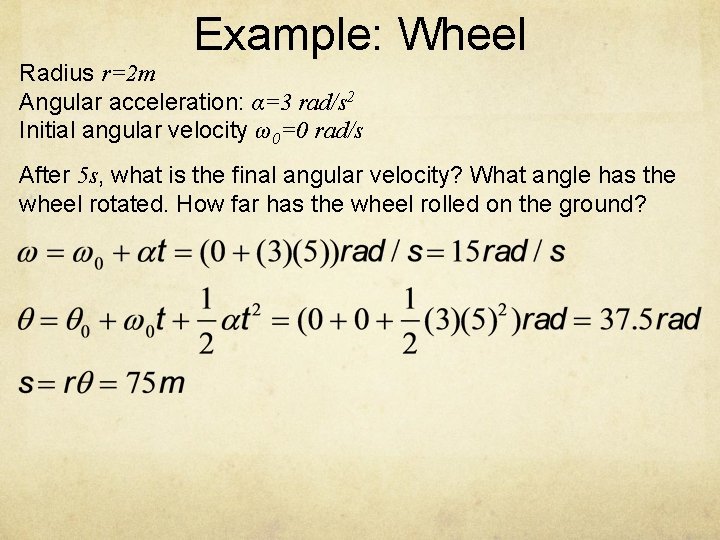
Example: Wheel Radius r=2 m Angular acceleration: α=3 rad/s 2 Initial angular velocity ω0=0 rad/s After 5 s, what is the final angular velocity? What angle has the wheel rotated. How far has the wheel rolled on the ground?
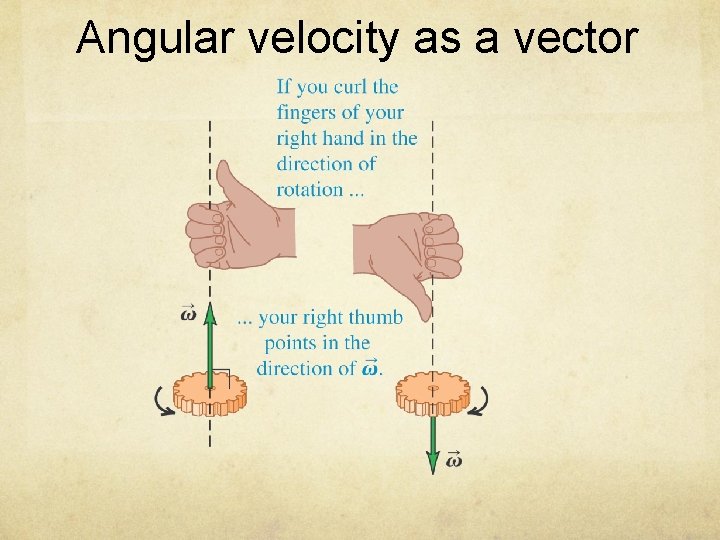
Angular velocity as a vector
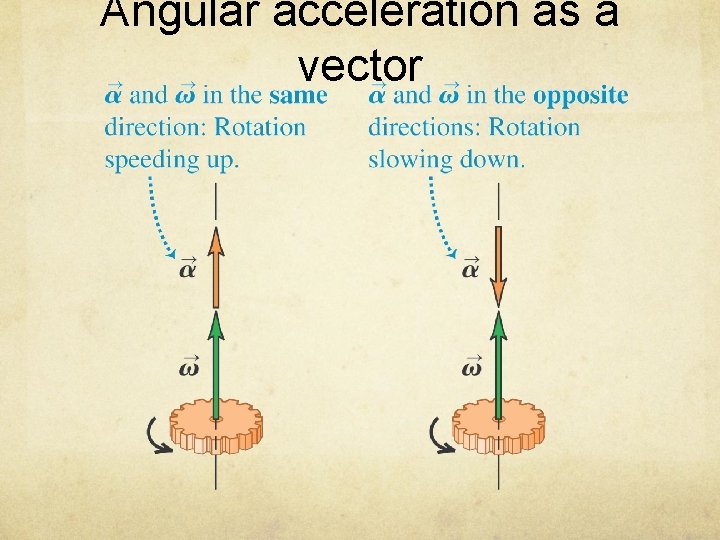
Angular acceleration as a vector
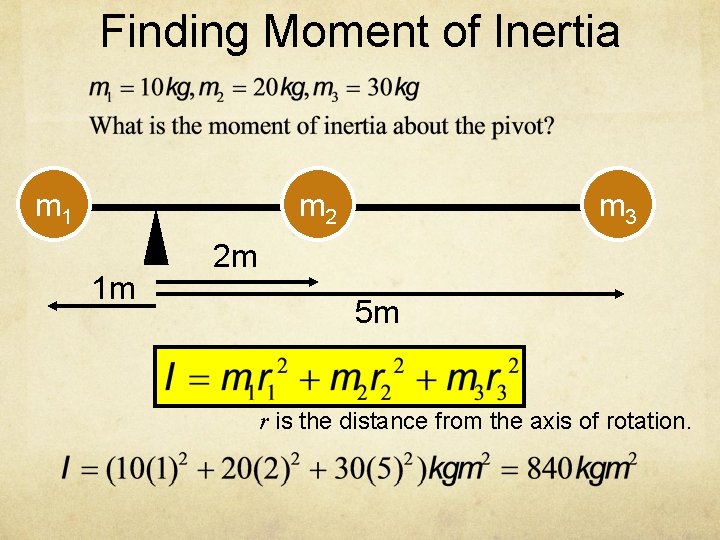
Finding Moment of Inertia m 1 m 2 1 m m 3 2 m 5 m r is the distance from the axis of rotation.
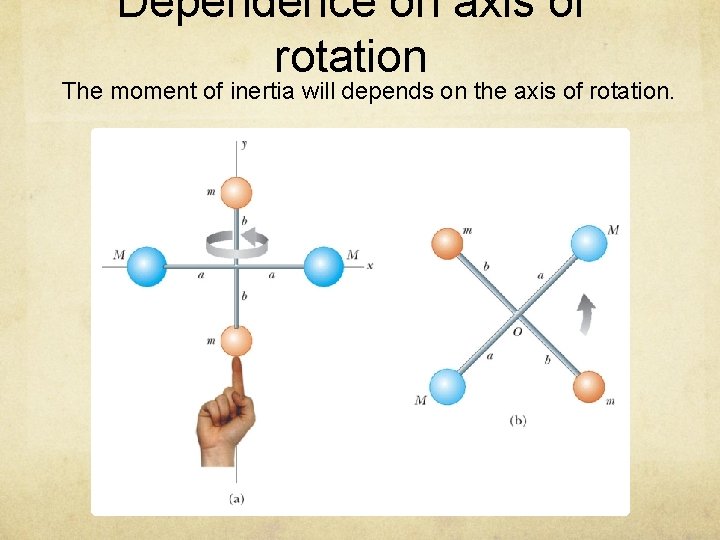
Dependence on axis of rotation The moment of inertia will depends on the axis of rotation.
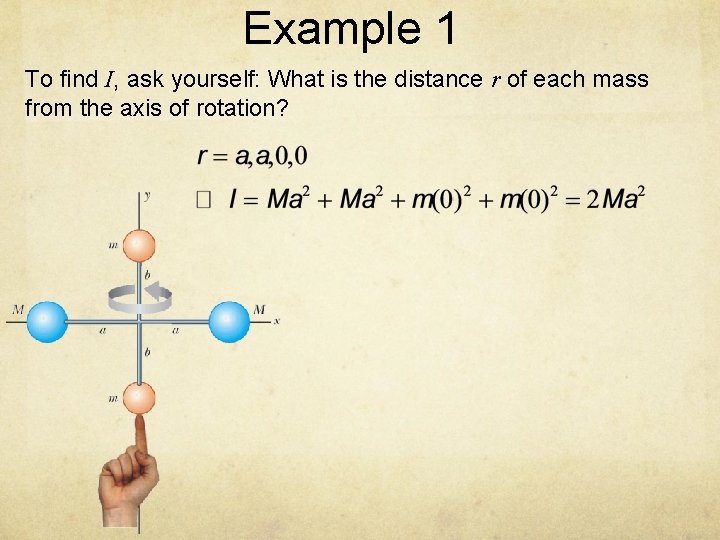
Example 1 To find I, ask yourself: What is the distance r of each mass from the axis of rotation?

Example 2 To find I, ask yourself: What is the distance r of each mass from the axis of rotation?
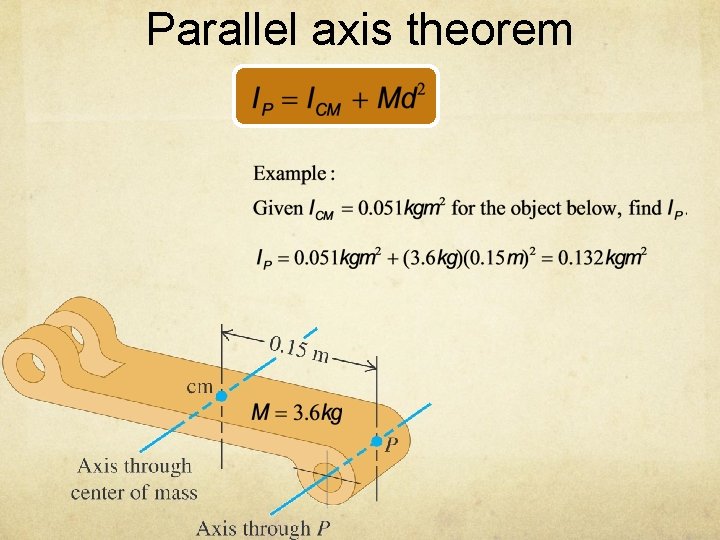
Parallel axis theorem
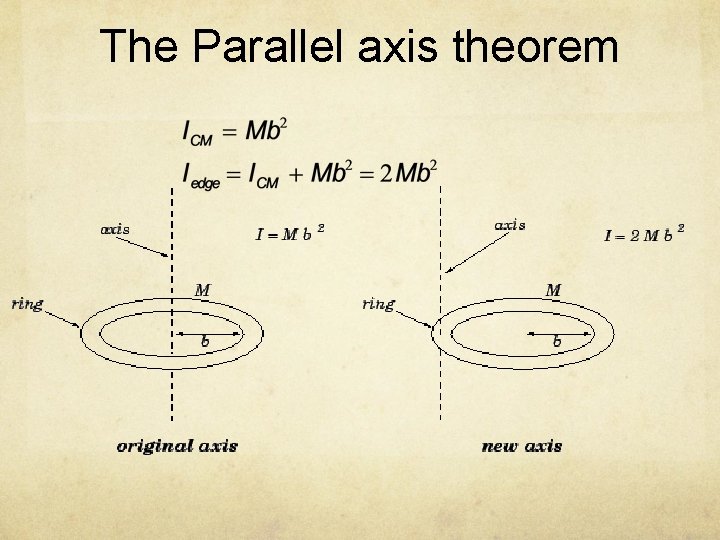
The Parallel axis theorem
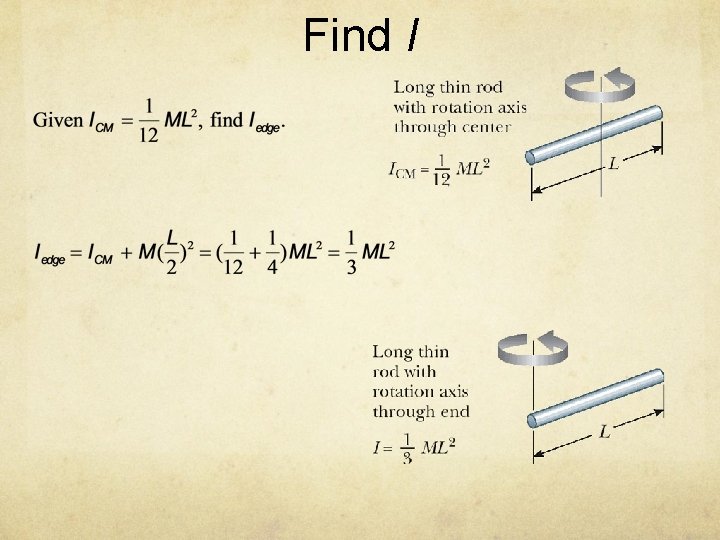
Find I

General formula for I Different objects with different geometry will have different formula for I. See the end of the lecture notes for detail.
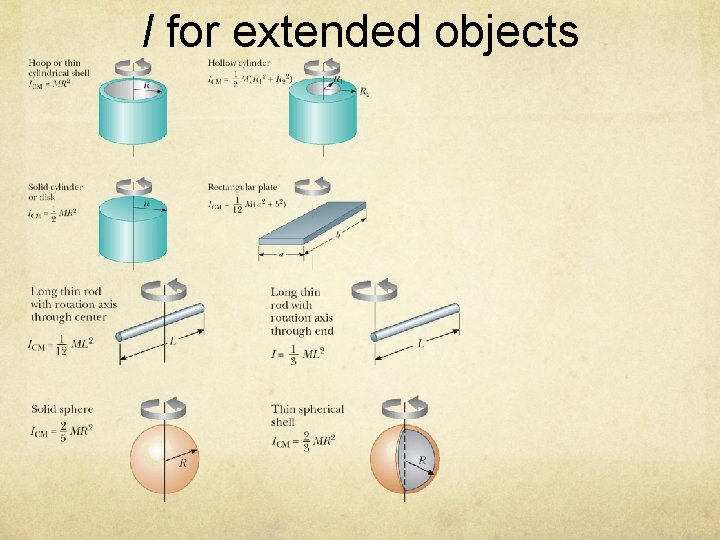
I for extended objects

Rotational Energy

Example
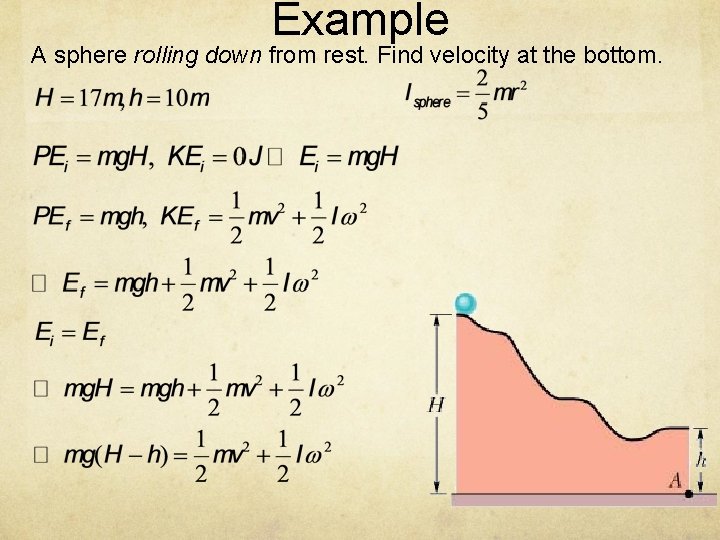
Example A sphere rolling down from rest. Find velocity at the bottom.

Example
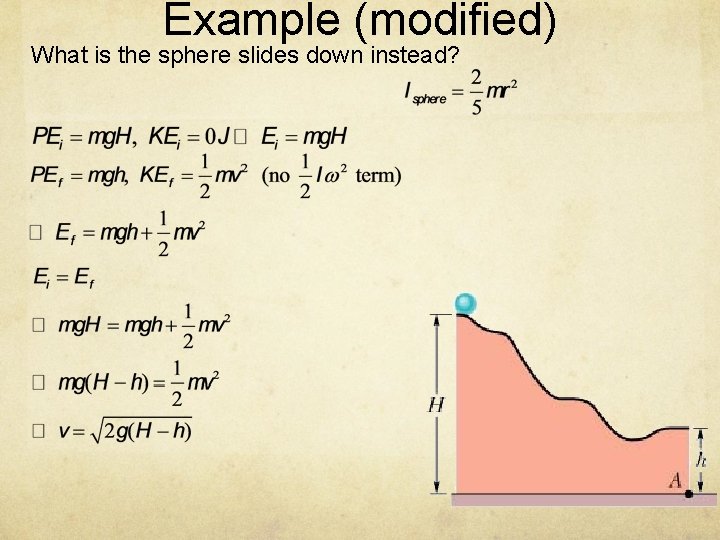
Example (modified) What is the sphere slides down instead?

Moment of inertia calculations Below we will use integration to calculate I for some basic geometrical objects.

Example: The Ring dm R ✕ “✕ ” represent rotational axis

Sequel: The Disk R r ✕ dm

Another Sequel: The Rod ✕ dm r Note that we defined the pivotal point to be on the left

Moving the pivotal point dm ✕ r What if I move the pivotal point to the middle?

Where you place the rotational axis matters!!! ✕ ≠ ✕

- Slides: 41