Chapter 9 Recursion Java Programming From Problem Analysis

Chapter 9: Recursion Java Programming: From Problem Analysis to Program Design (Chapter 14), Second Edition

Chapter Objectives s Learn about recursive definitions. s Explore the base case and the general case of a recursive definition. s Learn about recursive algorithms. s Learn about recursive methods. s Learn about how to use recursive methods to implement recursive algorithms. Java Programming: From Problem Analysis to Program Design, Second Edition 2

Introduction s // Program prints an array. public class Print { // print array iteratively public static void print. Iterative( int[] array ) { for (int i=0; i< array. length; ++i ) System. out. print(array[i] + " "); s } // end method print. Array Java Programming: From Problem Analysis to Program Design, Second Edition 3

s // recursively print array private static void print. Array. Helper( int[] array, int start. Index ) { if ( start. Index == array. length ) return; // print elements in normal order System. out. print( array[ start. Index ] + " " ); print. Array. Helper( array, start. Index + 1 ); } // end method print. Array. Helper Java Programming: From Problem Analysis to Program Design, Second Edition 4

s // recursively print array in reverse order private static void print. Array. Reverse. Helper( int[] array, int start. Index ) { if ( start. Index == array. length ) return; // print elements in reverse order print. Array. Reverse. Helper( array, start. Index + 1 ); System. out. print( array[ start. Index ] + " " ); } // end method print. Array. Helper Java Programming: From Problem Analysis to Program Design, Second Edition 5

s public static void main( String args[] ) { int array[] = { 8, 22, 88, 34, 84, 21, 94 }; System. out. print( "Array is: " ); print. Array. Helper( array, 0 ); // print array System. out. print( "Array in reverse order is: " ); print. Array. Reverse. Helper( array , 0 ); // print array in reverse order } Java Programming: From Problem Analysis to Program Design, Second Edition 6

Recursive Definitions s Recursion: s Process of solving a problem by reducing it to smaller versions of itself. Factorial of an integer: 0! = 1 n! = n * (n-1)! If n > 0 Java Programming: From Problem Analysis to Program Design, Second Edition 7

Recursive Definitions s Recursive definition: s Definition in which a problem is expressed in terms of a smaller version of itself. s Has one or more base cases. Java Programming: From Problem Analysis to Program Design, Second Edition 8

Recursive Definitions s Recursive algorithm: s Algorithm that finds the solution to a given problem by reducing the problem to smaller versions of itself. s Has one or more base cases. s Implemented using recursive methods. s Recursive method: s Method that calls itself. s Base case: s Case in recursive definition in which the solution is obtained directly. s Stops the recursion. Java Programming: From Problem Analysis to Program Design, Second Edition 9

Recursive Factorial Method public static int fact (int num) { if (num == 0) return 1; else return num * fact(num-1); } Java Programming: From Problem Analysis to Program Design, Second Edition 10

Recursive Factorial Method Java Programming: From Problem Analysis to Program Design, Second Edition 11

Tracing a Recursive Method Recursive method: s Has unlimited copies of itself. s Every recursive call has its own: s Code s Set of parameters s Set of local variables Java Programming: From Problem Analysis to Program Design, Second Edition 12

Tracing a Recursive Method s After completing a recursive call: s Control goes back to the calling environment. s Recursive call must execute completely before control goes back to previous call. s Execution in previous call begins from point immediately following recursive call. Java Programming: From Problem Analysis to Program Design, Second Edition 13

Designing Recursive Methods s Understand problem requirements. s Determine limiting conditions. ( ex: the number of elements in a list) s Identify base cases. Java Programming: From Problem Analysis to Program Design, Second Edition 14

Designing Recursive Methods s Provide direct solution to each base case. s Identify general cases. s Provide solutions to general cases in terms of smaller versions of general cases. Java Programming: From Problem Analysis to Program Design, Second Edition 15

Largest Value in Array public static int largest(int[] list, int lower. Index, int upper. Index) { int max; if (lower. Index == upper. Index) return list[lower. Index]; else { max = largest(list, lower. Index + 1, upper. Index); if (list[lower. Index] >= max) return list[lower. Index]; else return max; } } Java Programming: From Problem Analysis to Program Design, Second Edition 16

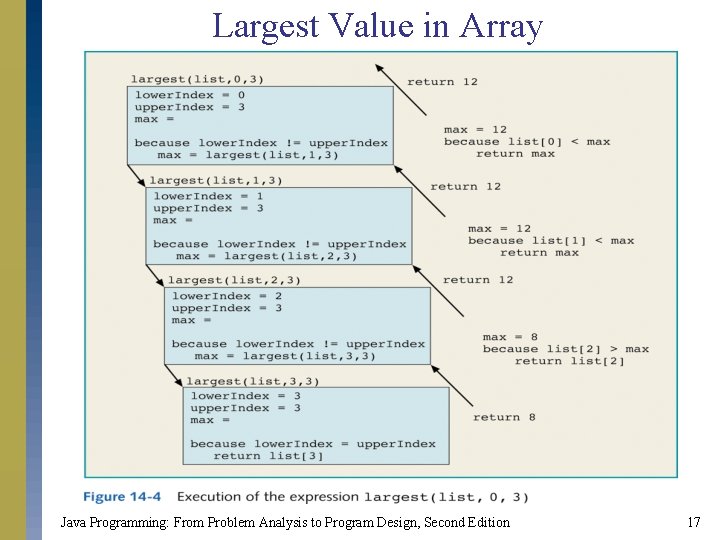
Largest Value in Array Java Programming: From Problem Analysis to Program Design, Second Edition 17

Recursion or Iteration? s Two ways to solve particular problem: s Iteration s Recursion s Iterative control structures use looping to repeat a set of statements. s Tradeoffs between two options: s Sometimes recursive solution is easier. s Recursive solution is often slower. Java Programming: From Problem Analysis to Program Design, Second Edition 18