Chapter 9 Probability Copyright 2016 2013 and 2010

9 -2 Multistage Experiments and Modeling Games Students will be able to understand explain: • Multistage experiments; • Independent events; • Conditional probability; and • Modeling games. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 2

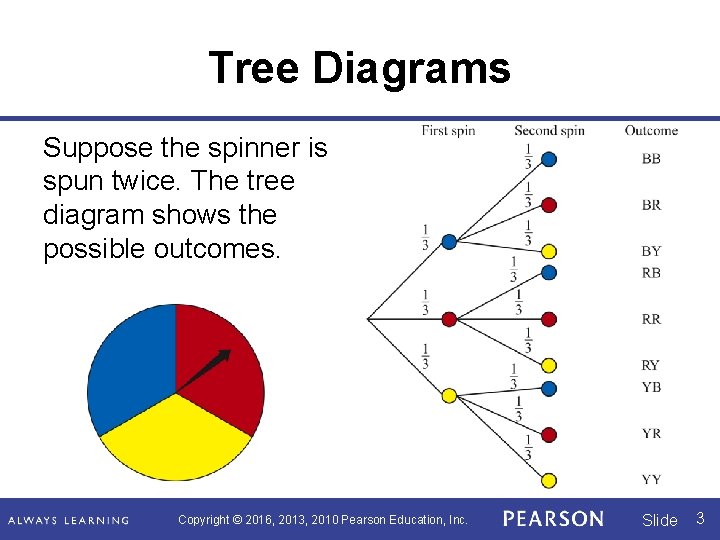
Tree Diagrams Suppose the spinner is spun twice. The tree diagram shows the possible

Tree Diagrams The sample space can be written {BB, BR, BY, RB, RR, RY,

Tree Diagrams Alternatively, we can generate the sample space using a table. YB Copyright

Example Suppose we toss a fair coin 3 times and record the results. Find each of the following: a. The sample space for this experiment. S = {HHH, HHT, HTH, THH, TTT, TTH, THT, HTT} b. The event A of tossing 2 heads and 1 tail A = {HHT, HTH, THH} Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 6

Example (continued) c. The event B of tossing no tails. B = {HHH} d. The event C of tossing a head on the last toss C = {HHH, HTH, THH, TTH} Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 7

Example a. When rolling a pair of fair dice, find the probability of the event A = rolling double sixes. There are 36 possible rolls. There is only one way to roll double sixes. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 8

Example (continued) b. Find the probability of rolling a sum of 7 or 11

Example (continued) There are 6 ways to form a sum of “ 7”, so

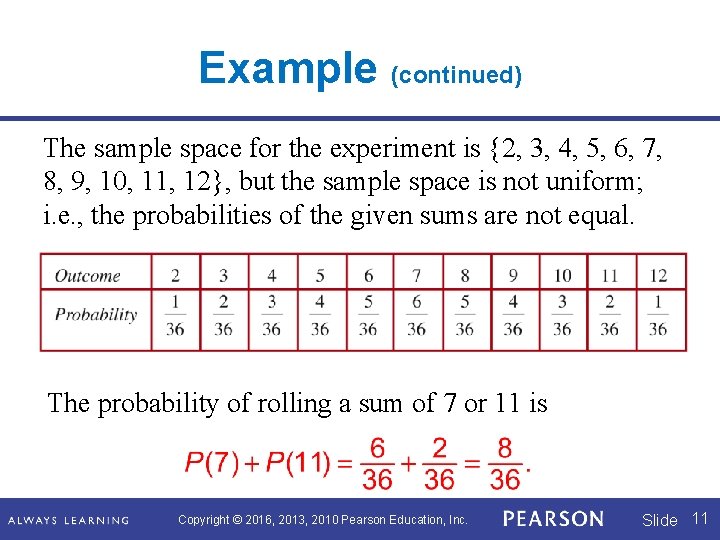
Example (continued) The sample space for the experiment is {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}, but the sample space is not uniform; i. e. , the probabilities of the given sums are not equal. The probability of rolling a sum of 7 or 11 is Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 11

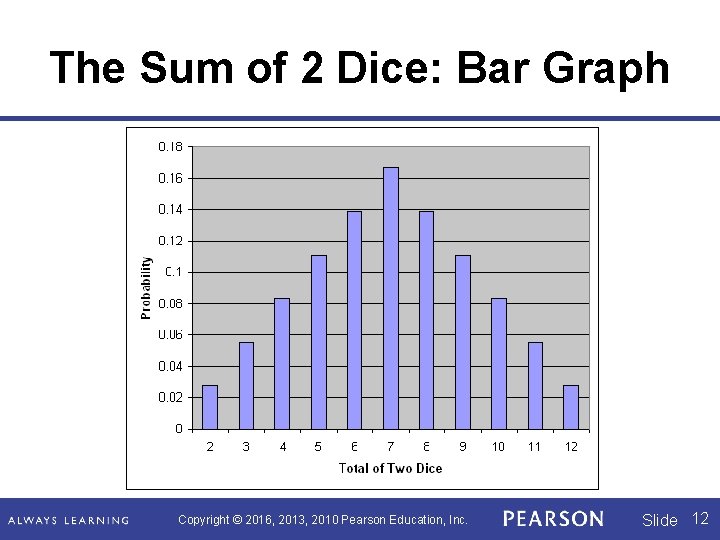
The Sum of 2 Dice: Bar Graph Copyright © 2016, 2013, 2010 Pearson Education,

Example A fair pair of dice is rolled. Let E be the event of rolling a sum that is an even number and F the event of rolling a sum that is a prime number. Find the probability of rolling a sum that is even or prime, that is, P(E U F). E U F = {2, 4, 6, 8, 10, 12, 3, 5, 7, 11} Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 13

Example (continued) Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 14

Example (continued) Alternate solution 1: E = {2, 4, 6, 8, 10, 12} and F = {2, 3, 5, 7, 11}. Thus, E and F are not mutually exclusive because E ∩ F = {2}. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 15

Example (continued) Alternate solution 2: E = {2, 4, 6, 8, 10, 12} and F = {2, 3, 5, 7, 11}. Thus, E U F = {2, 3, 4, 5, 6, 7, 8, 10, 11, 12} and E U F = {9}. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 16

More Multistage Experiments The box in figure (a) contains one black ball and two white balls. If a ball is drawn at random and the color recorded, a tree diagram for the experiment might look like the one in figure (b). Because each ball has the same chance of being drawn, we may combine the branches and obtain the tree diagram shown in figure (c). Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 17

Suppose a ball is drawn at random from the box in the figure and its color recorded. The ball is then replaced, and a second ball is drawn and its color recorded. The sample space for this twostage experiment may be recorded using ordered pairs as Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 18

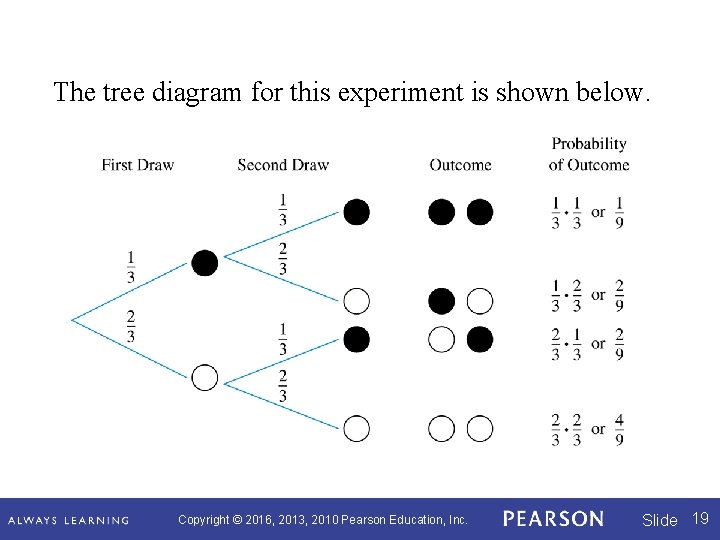
The tree diagram for this experiment is shown below. Copyright © 2016, 2013, 2010

Multiplication Rule for Probabilities for Tree Diagrams For all multistage experiments, the probability of the outcome along any path of a tree diagram is equal to the product of all the probabilities along the path. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 20

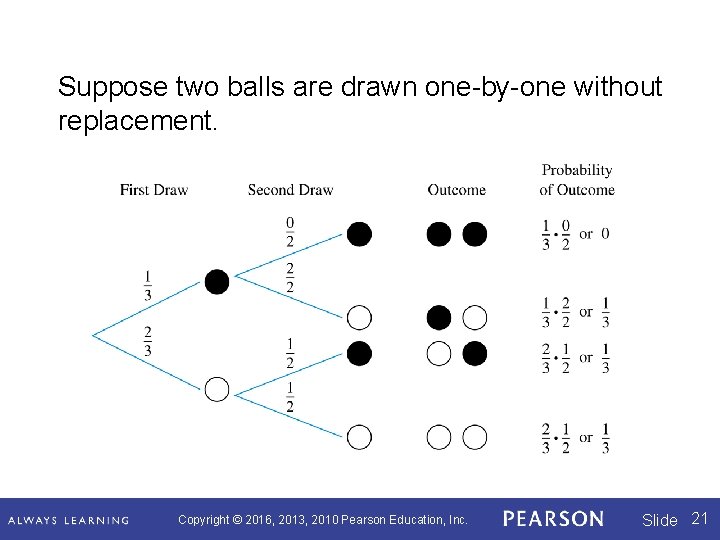
Suppose two balls are drawn one-by-one without replacement. Copyright © 2016, 2013, 2010 Pearson

Independent Events Independent events: When the outcome of one event has no influence on

Independent Events If two coins are flipped and event E 1 is obtaining a head on the first coin and E 2 is obtaining a tail on the second coin, then E 1 and E 2 are independent events because one event has no influence on possible outcomes. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 23

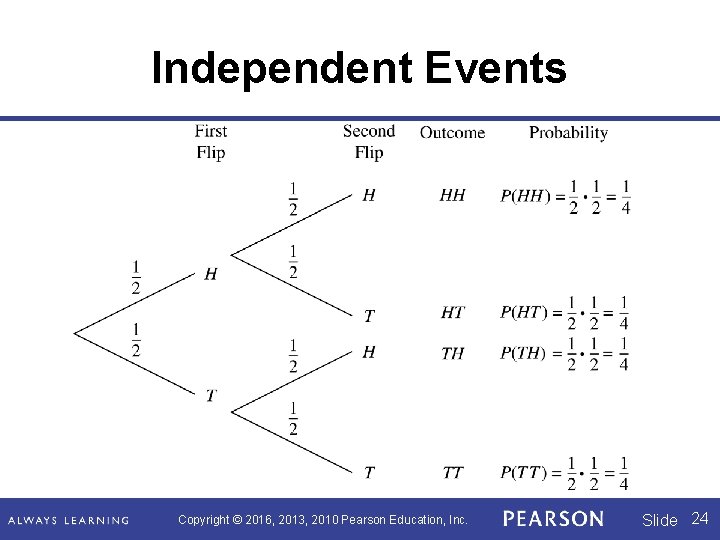
Independent Events Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 24

Independent Events For any independent events E 1 and E 2, Copyright © 2016,

Example The figure shows a box with 11 letters. Some letters are repeated. Suppose 4 letters are drawn at random from the box one-by-one without replacement. What is the probability of the outcome BABY, with the letters chosen in exactly the order given? Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 26

Example (continued) We are interested in only the tree branch leading to the outcome BABY. The probability of the first B is B’s out of 11 letters. because there are 2 The probability of the second B is because there are 9 letters left after 1 B and 1 A have been chosen. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 27

Example Consider the three boxes shown below. A letter is drawn from box 1 and placed in box 2. Then, a letter is drawn from box 2 and placed in box 3. Finally, a letter is drawn from box 3. What is the probability that the letter drawn from box 3 is B? (Call this event E. ) Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 28

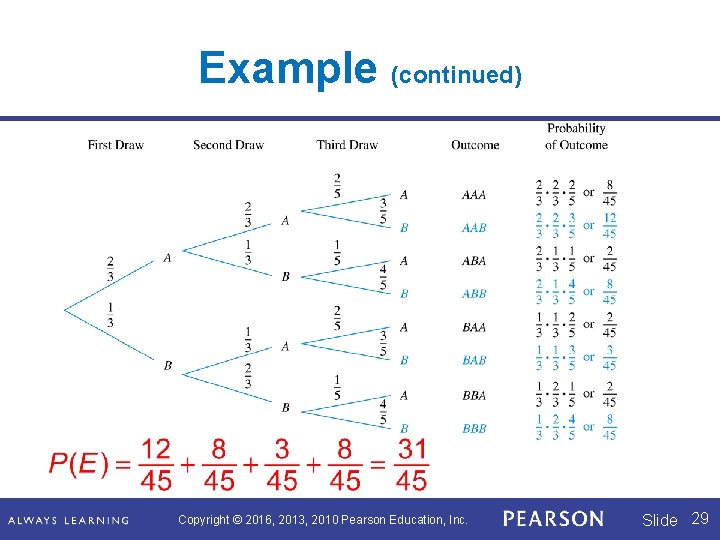
Example (continued) Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 29

Conditional Probabilities If A and B are events in sample space S and P(A) 0, then the conditional probability that an event B occurs given that event A has occurred is given by Copyright © 2016, 2013, 2010 Pearson Education, Inc. Copyright © 2013, 2010, and 2007, Pearson Education, Inc. Slide 30

Example What is the probability of rolling a 6 on a fair die if you know that the roll is an even number? If event B is rolling a 6 and event A is rolling an even number, then Copyright © 2016, 2013, 2010 Pearson Education, Inc. Copyright © 2013, 2010, and 2007, Pearson Education, Inc. Slide 31

Modeling Games There are two black marbles and one white marble in a box. Gwen mixes the marbles, and Arthur draws two marbles at random without replacement. If the two marbles match, Arthur wins; otherwise, Gwen wins. Does each player have an equal chance of winning? Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 32

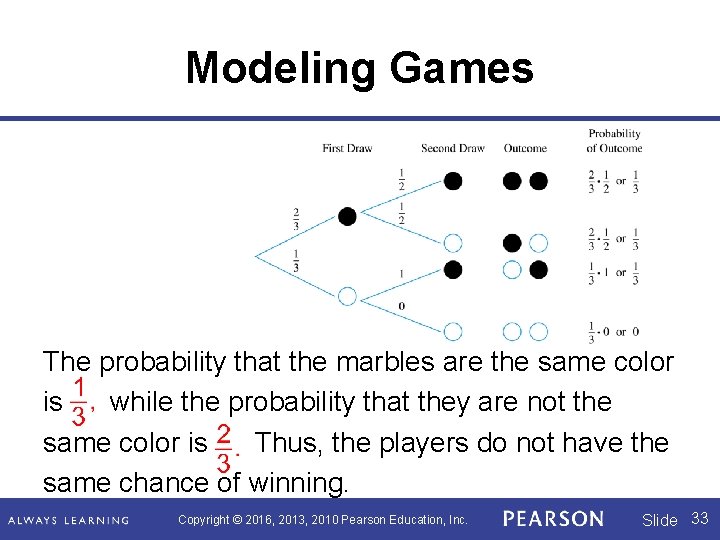
Modeling Games The probability that the marbles are the same color is while the probability that they are not the same color is Thus, the players do not have the same chance of winning. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 33