Chapter 9 Morphological Image Processing Preview Morphology denotes

Chapter 9 Morphological Image Processing

Preview Morphology: denotes a branch of biology that deals with the form and structure of animals and plants. Mathematical morphology: tool for extracting image components that are useful in the representation and description of region shapes. Filtering, thinning, pruning.

Scope Will focus on binary images. Applicable to other situations. (Higherdimensional space)

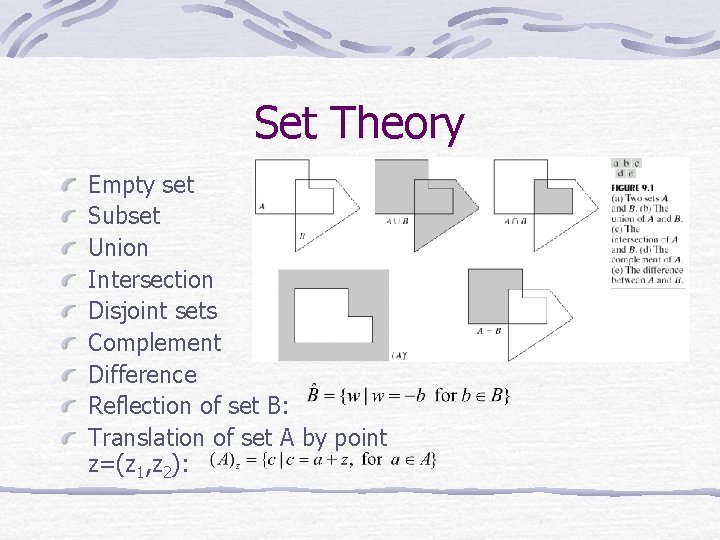
Set Theory Empty set Subset Union Intersection Disjoint sets Complement Difference Reflection of set B: Translation of set A by point z=(z 1, z 2):

Logic Operations AND OR NOT

Dilation With A and B as sets in Z 2, the dilation of A by B is defined as: Or, equivalently, B is commonly known as the structuring element.

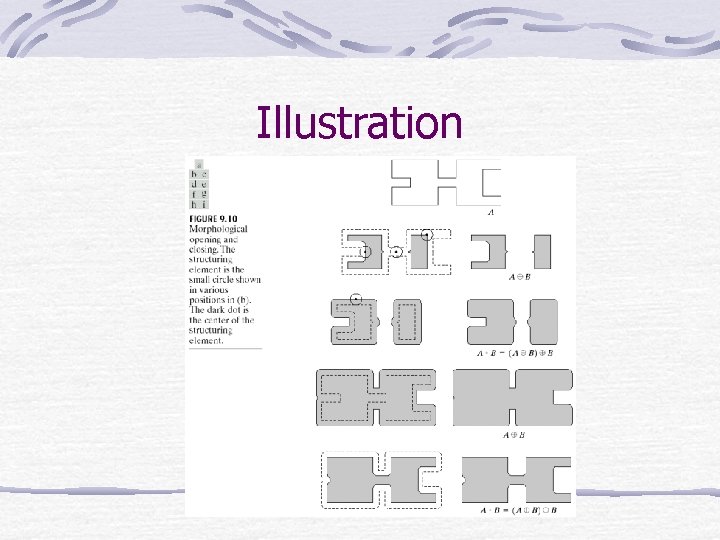
Illustration

Example

Erosion With A and B as sets in Z 2, the erosion of A by B is defined as: Dilation and erosion are duals:

Illustration

Example: Removing image components

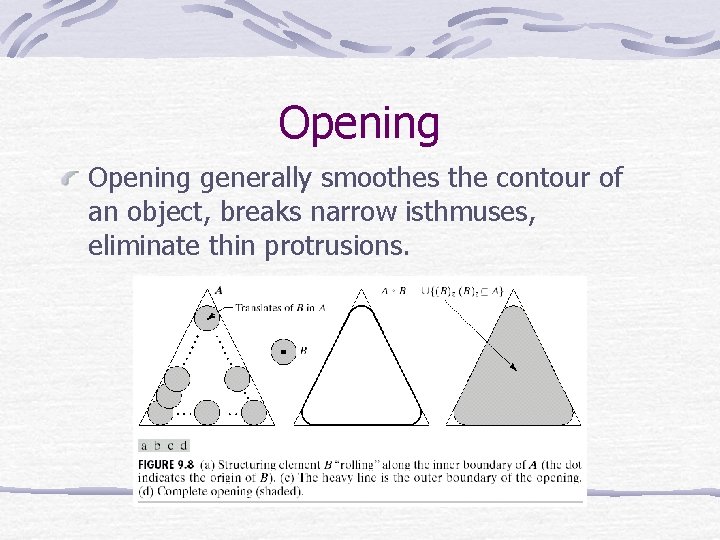
Opening and Closing Opening of set A by structuring element B: Erosion followed by dilation Closing of set A by structuring element B: Dilation followed by erosion

Opening generally smoothes the contour of an object, breaks narrow isthmuses, eliminate thin protrusions.

Closing tends to smooth contours, fuse narrow breaks and long thin gulfs, eliminate small holes, fill gaps in the contour.

Illustration

Example

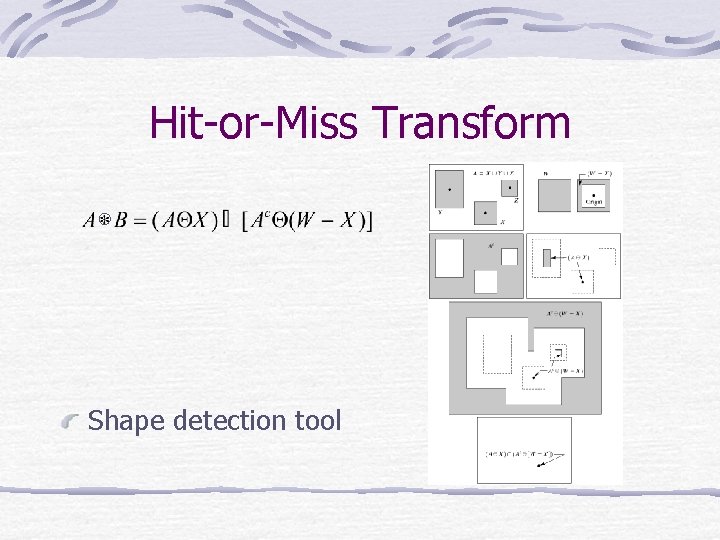
Hit-or-Miss Transform Shape detection tool

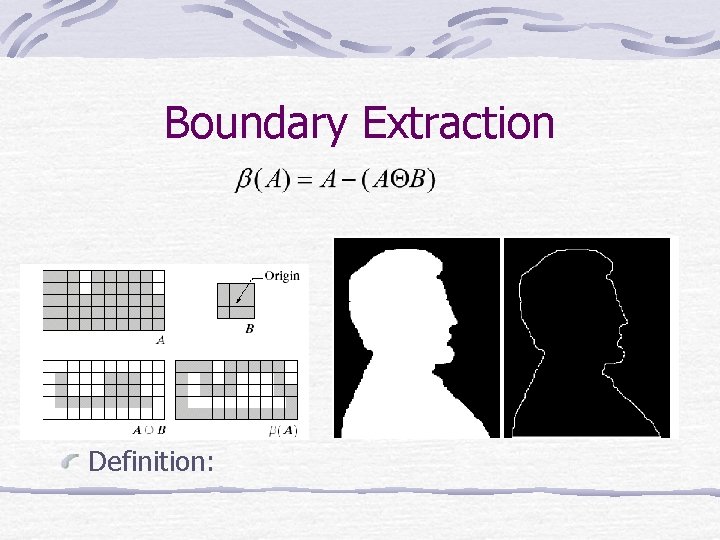
Boundary Extraction Definition:

Region Filling Beginning with a point p inside the boundary, repeat: with X 0=p Until Xk=Xk-1 Conditional dilation

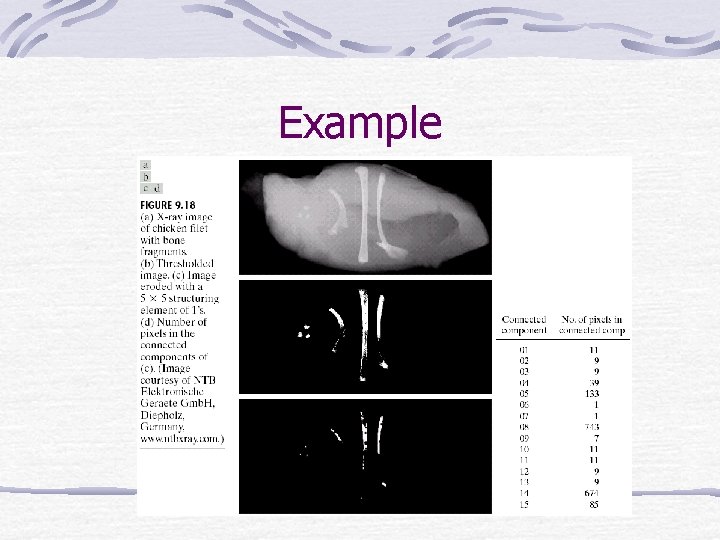
Example

Extraction of Connected Component Beginning with a point p of the connected component, repeat: with X 0=p Until Xk=Xk-1 The connected component Y=Xk

Illustration

Example

Convex Hull A set A is said to be convex if the straight line segment joining any two points in A lies entirely within A. The convex hull H of an arbitrary set S is the smallest convex set containing S. H-S is called the convex deficiency of S. C(A): convex hull of a set A.

Algorithm Four structuring elements: Bi, i=1, 2, 3, 4 Repeat with X 0 i =A until Xki=Xk-1 i to obtain Di The convex hull of A is:

Illustration

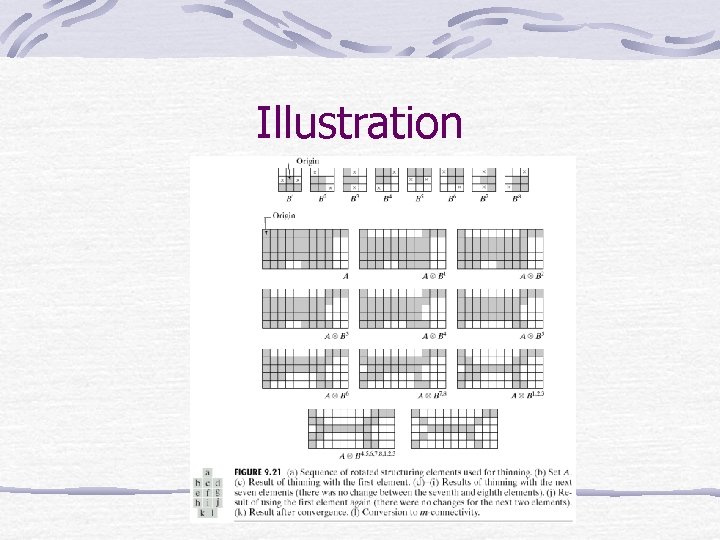
Thinning The thinning of a set A by a structuring element B is defined as:

Illustration

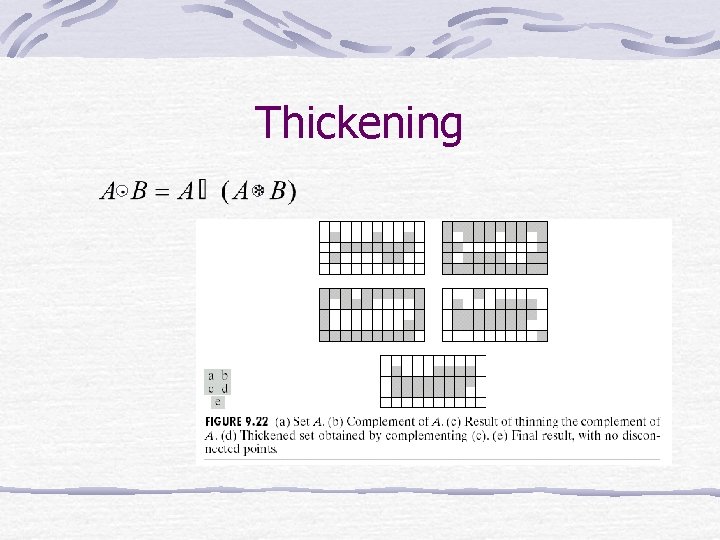
Thickening

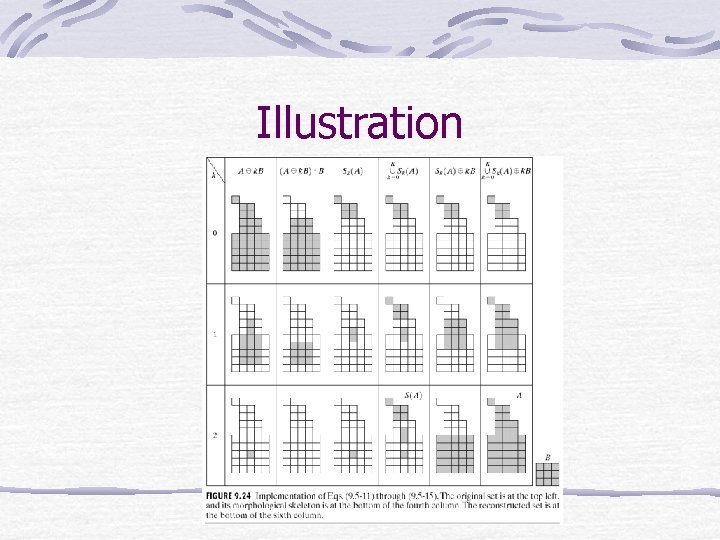
Skeleton

Skeleton: Definition

Illustration

Pruning

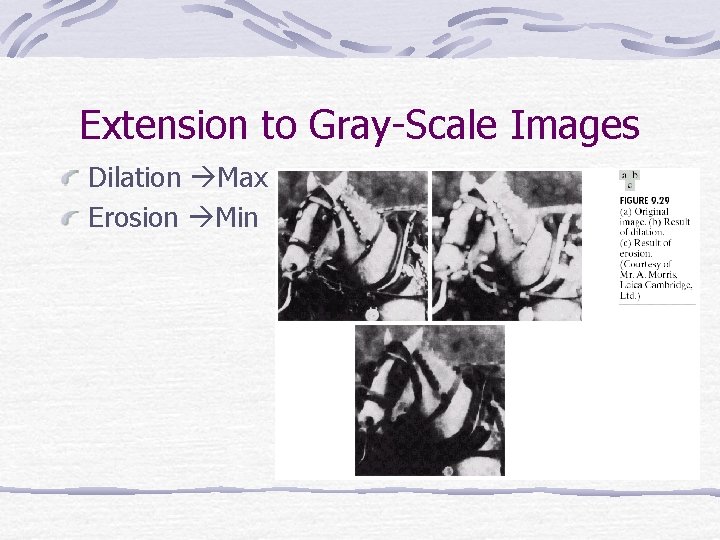
Extension to Gray-Scale Images Dilation Max Erosion Min

Illustration

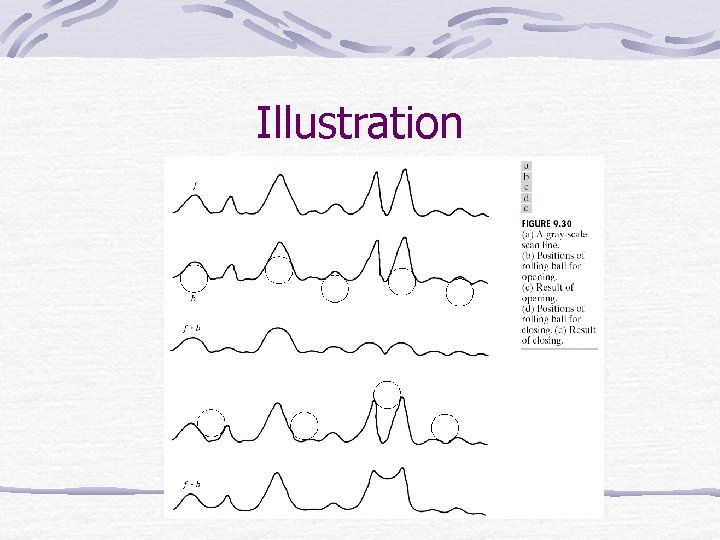
Opening and Closing

Smoothing and Gradient