Chapter 9 Molar phase diagrams molar phase diagram

Chapter 9 Molar phase diagrams

• molar phase diagram : what happens if the potentials in a phase diagram are replaced by their conjugate molar quantities? i. d. potential axis replaced by axis - a single phase field : the same general shape in a molar phase diagram - a two-phase region : phases in equil with each other will no longer fall on the same - the same pt same values of T, -P, mi in both phases, however the molar quantities are different between phases they are connected by a or konode (in Germany) in a molar phase diagram • why separated ? at equil in the T, -P, mi diagram, on the surface of G-D, Ta =Tb, -Pa =-Pb but Sma≠Smb, Vma≠Vmb in G-D,

In considering two phases, a and b in equil with each other, the system is then moved away from equil by changing the value of one potential, Yj supposing α is the phase favored by increased Yj value 곧 만큼의 차이 (difference) 가 나타난다 (shows up in the molar phase diagram). 에

• Fig. 9. 1 T Sm (const P, tie-line perpendicular to -P axis) -P Vm (const T, tie-line perpendicular to T axis) likewise, if m. B XB(=NB/NA) then the same happens one-phase fields separate and leave room for a field

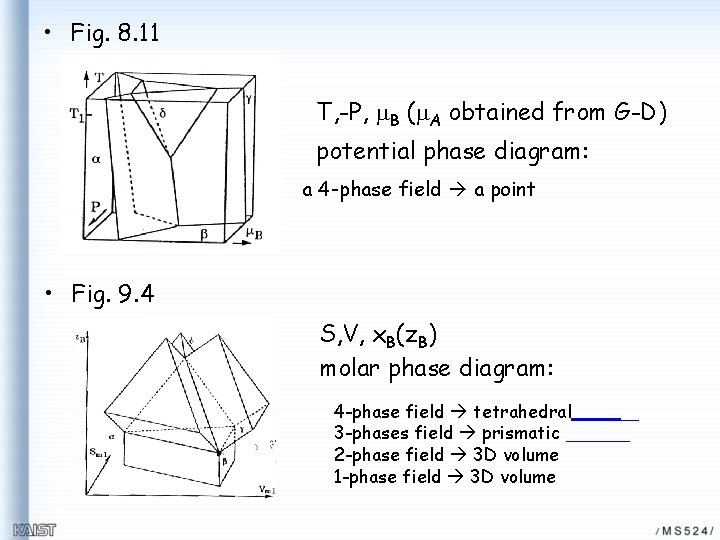
• Fig. 8. 11 T, -P, m. B (m. A obtained from G-D) potential phase diagram: a 4 -phase field a point • Fig. 9. 4 S, V, x. B(z. B) molar phase diagram: 4 -phase field tetrahedral 3 -phases field prismatic 2 -phase field 3 D volume 1 -phase field 3 D volume

The topology of potential phase diagrams is very simple and each geometrical element is a. A phase diagram with only molar axes have a relatively simple topology. All the phase fields have the same as the diagram itself. For the unary system all the phase fields have 2 D and for the binary system they have 3 D.

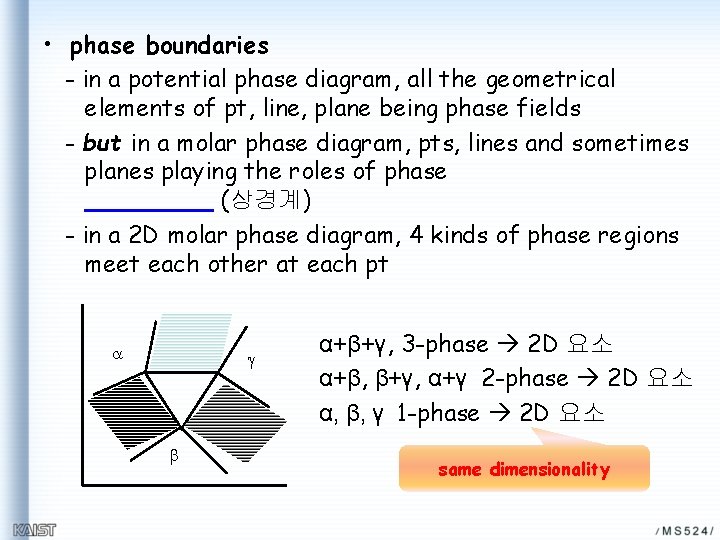
• phase boundaries - in a potential phase diagram, all the geometrical elements of pt, line, plane being phase fields - but in a molar phase diagram, pts, lines and sometimes planes playing the roles of phase (상경계) - in a 2 D molar phase diagram, 4 kinds of phase regions meet each other at each pt a g b α+β+γ, 3 -phase 2 D 요소 α+β, β+γ, α+γ 2 -phase 2 D 요소 α, β, γ 1 -phase 2 D 요소 same dimensionality

• in a 3 D molar diagram a four-phase region : a+b+g+z each corner of a tetrahedron being connected to a one-phase field for example, at the pt related with b single phase (Fig. 9. 4) 8 regions, 8 phase fields 4 -phase : 1 region → a+b+g+z 3 -phase : 3 regions → a+b+g, b+g+z, a+b+z 2 -phases : 3 regions → a+b, b+g, b+z 1 -phase : 1 region → b ∴ two molar axes insert Fig. 9. 8 Fig. 8. 5 (a) Elementary unit of a phase diagram with two molaraxes. (b) Topological equivalence. three molar axes insert Fig. 9. 9 Fig. 8. 6 Elemetary unit of a phase diagram with three molar axes.

• in a 2 D molar diagram, Masing (1949) → the # of phases in the phase fields changes by one unit in crossing a linear phase boundary • generalization by Palatnik and Landau (1964) D + + D- = r - b (MPL boundary rule) D+ : # of phase that appear D- : # of phase that disappear r : # of axes in the molar diagram b : dimensionality of the phase boundary crossed • special phase boundaries liquid / liquid + solid / solid 1+ solid 2

• sections of molar phase diagrams - for practical reasons one likes to reduce the # of axes in a complete molar phase diagram - sectioning at a constant value of a molar variable : isoplethal section or - MPL boundary rule applicable to the sections ∵ r – b not changing by sectioning (r – b : r and b decreases by 1, respectively, each sectioning, in the same way for ns sectioning) ex) 3 D (1 sectioning) → 2 D r=3→ 2 phase boundary : volume b=3→ 2 phase boundary : plane b=2→ 1 phase boundary : line b=1→ 0

• Fig. 9. 11 ⓐ ⓑ ⓒ in the elementary unit of a molar phase diagram sectioned a sufficient # of times to make it 2 D case of ⓐ, D+ + D- = r – b = 2 (2 D) - 1 (line) = 1 ∴ e-1 e or e-2 case of ⓑ, D+ + D- = r – b = 2 (2 D) - 1 (line) = 1 ∴ e e+1 or e-1 e-2 e-1 or e-3 case of ⓒ, D+ + D- = r – b = 2 (2 D) – 0 (pt) = 2 ∴ e+1 D+ = 2, D- = 0 e-1 D+ = 1, D- = 1 e-3 D+ = 0, D- = 2 which one is true in this case ? see the next slide!

• Schreinemakers’ rule (1912) - at const T & P, for isobarothermal sections of ternary diagrams, extrapolations of one-phase field boundaries must either both fall inside three-phase fields or one inside each of two-phase fields - Hillert (1985) generalized this in molar phase diagram Schreinemacher under const T & P ∴ Gibbs free energy (G) be used Hillert generalized molar diagram ∴ based upon U (internal energy)

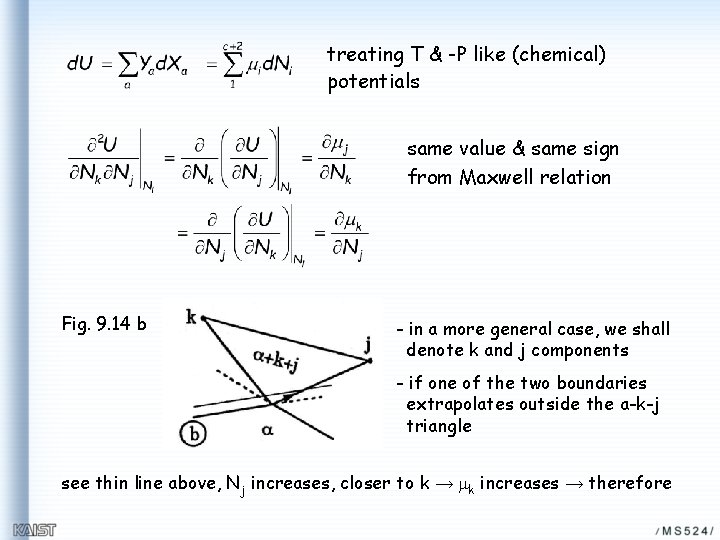
treating T & -P like (chemical) potentials same value & same sign from Maxwell relation Fig. 9. 14 b - in a more general case, we shall denote k and j components - if one of the two boundaries extrapolates outside the a-k-j triangle see thin line above, Nj increases, closer to k → mk increases → therefore

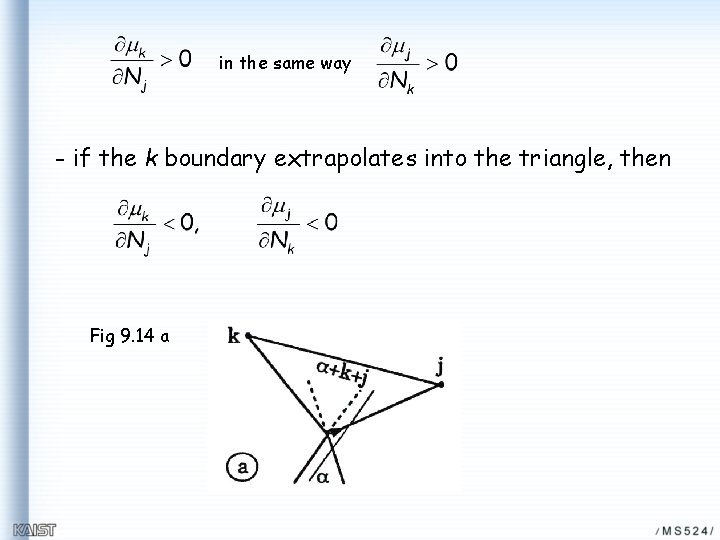
in the same way - if the k boundary extrapolates into the triangle, then Fig 9. 14 a

- this rule applicable to equipotential sections (at const T & P) as well as mixed phase diagram Fig. 9. 15 (the rule being satisfied at all the intersections in this diagram) - it may be used as a convenient guide when other information is lacking

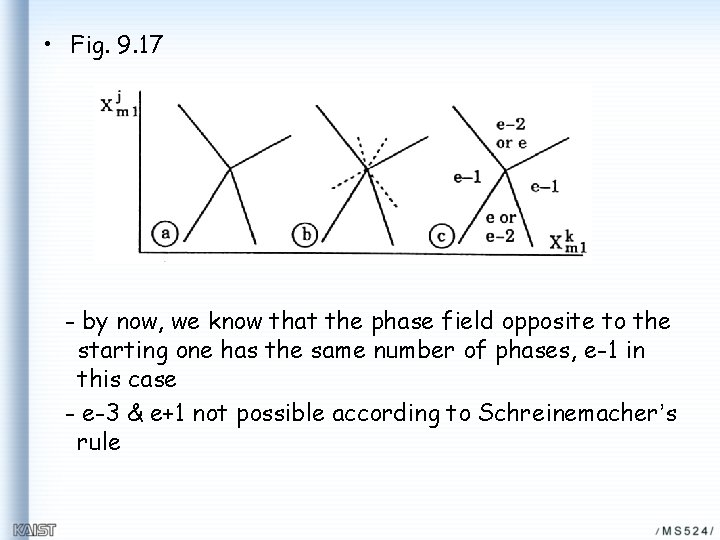
• Fig. 9. 17 - by now, we know that the phase field opposite to the starting one has the same number of phases, e-1 in this case - e-3 & e+1 not possible according to Schreinemacher’s rule