Chapter 9 Logistic Regression Learning Objectives How to

Chapter 9 Logistic Regression

Learning Objectives • How to use logistic regression to describe an interval-level independent relationship with a dichotomous dependent variable • How logit is similar and different from OLS regression • How maximum likelihood estimation (MLE) works • How to use logit with multiple independent variables • How to use probabilities to interpret logistic regression results

• If both the DV and the IV are interval OLS or linear regression is the appropriate model to use • If the DV is a dichotomous variable then we will need to use logistic regression • A binary variable or a dichotomous variable or a dummy variable- has two values 0/1. For example no war/ war, no peace/peace, did not vote/voted, not a smoker/smoker etc. These two categories must be mutually exclusive.

Logistic regression • When we perform OLS regression we can safely assume that there is a linear relationship between the DV and the IV • In logistic regression we cannot assume a linear relationship

• Suppose we are investigating whether education (x) has an effect on voter turnout (y) among a random sample of 500 respondents. • We can assume that education is an ordinal variable with four categories of education low-high and voter turnout is a binary variable with voting equal to 1 and not voting equal to 0.

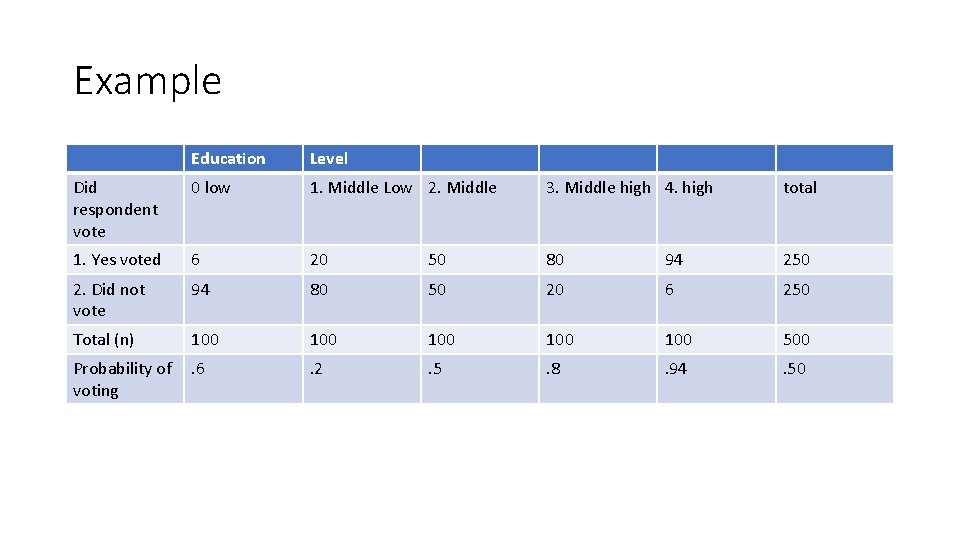
Example Education Level Did respondent vote 0 low 1. Middle Low 2. Middle 3. Middle high 4. high total 1. Yes voted 6 20 50 80 94 250 2. Did not vote 94 80 50 20 6 250 Total (n) 100 100 100 500 Probability of voting . 6 . 2 . 5 . 8 . 94 . 50

• When using logistic regression you need to think in terms of probabilities. The probability of something happening. • Suppose that you make $10, 000 per year and were trying to decide to buy a house or not. Only making 10, 000 per year you probably will not buy a house. No what if your salary increases to $20, 000 a year, the probability of purchasing a house may not increase much at all, but if your salary increased to $75000 per year, the probability will most likely increase drastically.

• Probabilities are based on the number of occurrences of outcomes divided by the total number of outcomes • Odds- based on the number of occurrences of one outcome divided by the number of occurrences of other outcomes • Odds=probability / (1 -probability)

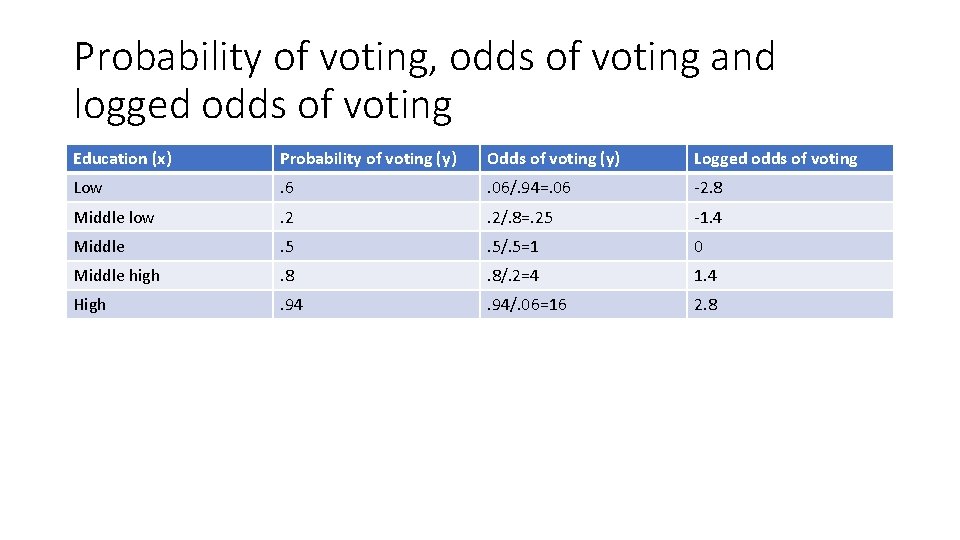
Probability of voting, odds of voting and logged odds of voting Education (x) Probability of voting (y) Odds of voting (y) Logged odds of voting Low . 6 . 06/. 94=. 06 -2. 8 Middle low . 2/. 8=. 25 -1. 4 Middle . 5/. 5=1 0 Middle high . 8/. 2=4 1. 4 High . 94/. 06=16 2. 8

• Percentage change in the odds- take the change between two categories and divided it by the probability of the lower category and that gives the percent of change in the odds • The odds move from. 6 to. 25 which is an increase of. 19 divided by. 06= 3. 17 = 317% increase

• Common logarithms are called base 10 logs and are used in electronics and experimental sciences • Base-e logs are called natural logarithms and are typically used by statisticians. Base-e logs are called natural and are typically abbreviated ln • The natural log of 100 for example is 4. 61 because 100 equals the base e raised to the power 4. 61 • Any number less than 1 has a negatively signed log so to express as a natural log we would raise the base e to a negative power -1. 4 • Natural logged odds transformations are often called logit transformations or logits

Maximum Likelihood estimation • Maximum likelihood estimation takes the sample wide probability of observing a specific value of a binary dependent variable and sees how well this probability predicts that outcome for each individual case in the sample • Likelihood function- is a number that summarizes how well a models prediction fits the observed data