Chapter 9 Linear Momentum Systems of Particles and

Chapter 9 Linear Momentum, Systems of Particles, and Collisions

Linear momentum (Ch. 4) • Linear momentum (or, simply momentum) point-like object (particle) is of a • SI unit of linear momentum is kg*m/s • Momentum is a vector, its direction coincides with the direction of velocity

Newton’s Second Law revisited (Ch. 4) • Originally, Newton formulated his Second Law in a more general form • The rate of change of the momentum of an object is equal to the net force acting on the object • For a constant mass

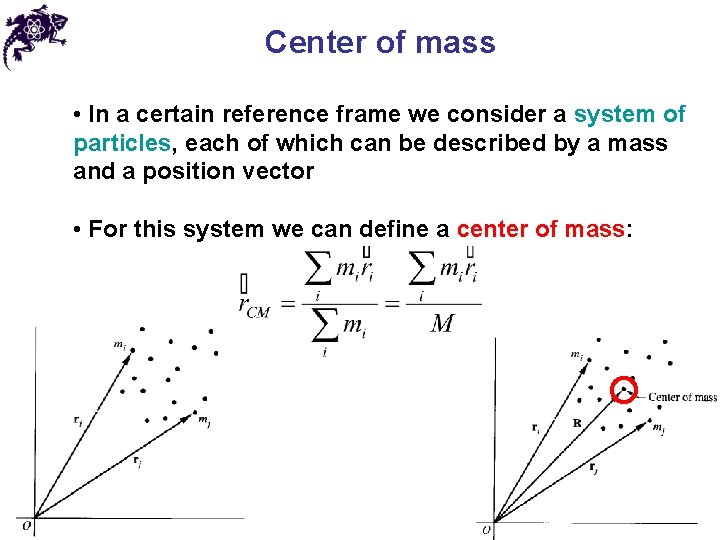
Center of mass • In a certain reference frame we consider a system of particles, each of which can be described by a mass and a position vector • For this system we can define a center of mass:

Center of mass of two particles • A system consists of two particles on the x axis • Then the center of mass is

Center of mass of a rigid body • For a system of individual particles we have • For a rigid body (continuous assembly of matter) with volume V and density ρ(V) we generalize a definition of a center of mass:

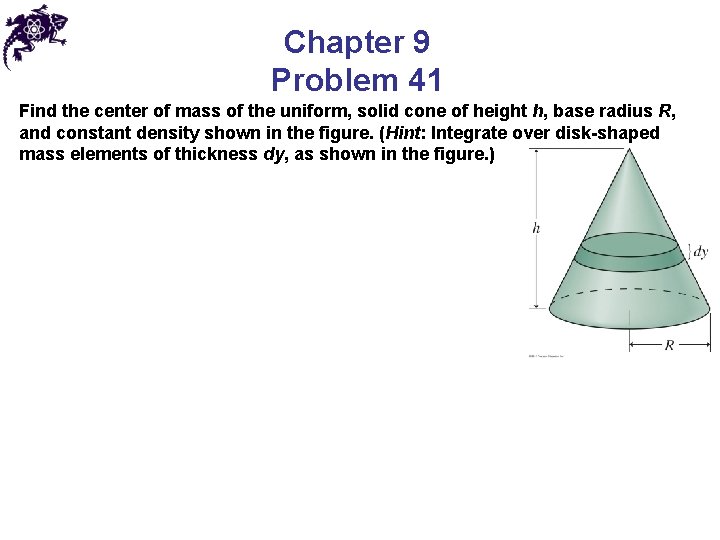
Chapter 9 Problem 41 Find the center of mass of the uniform, solid cone of height h, base radius R, and constant density shown in the figure. (Hint: Integrate over disk-shaped mass elements of thickness dy, as shown in the figure. )

Newton’s Second Law for a system of particles • For a system of particles, the center of mass is • Then

Newton’s Second Law for a system of particles • From the previous slide: • Here is a resultant force on particle i • According to the Newton’s Third Law, the forces that particles of the system exert on each other (internal forces) should cancel: • Here is the net force of all external forces that act on the system (assuming the mass of the system does not change)

Newton’s Second Law for a system of particles

Linear momentum for a system of particles • We define a total momentum of a system as: • Using the definition of the center of mass • The linear momentum of a system of particles is equal to the product of the total mass of the system and the velocity of the center of mass

Linear momentum for a system of particles • Total momentum of a system: • Taking a time derivative • Alternative form of the Newton’s Second Law for a system of particles

Conservation of linear momentum • From the Newton’s Second Law • If the net force acting on a system is zero, then • If no net external force acts on a system of particles, the total linear momentum of the system is conserved (constant) • This rule applies independently to all components

Chapter 9 Problem 17 A popcorn kernel at rest in a hot pan bursts into two pieces, with masses 91 mg and 64 mg. The more massive piece moves horizontally at 47 cm/s. Describe the motion of the second piece.

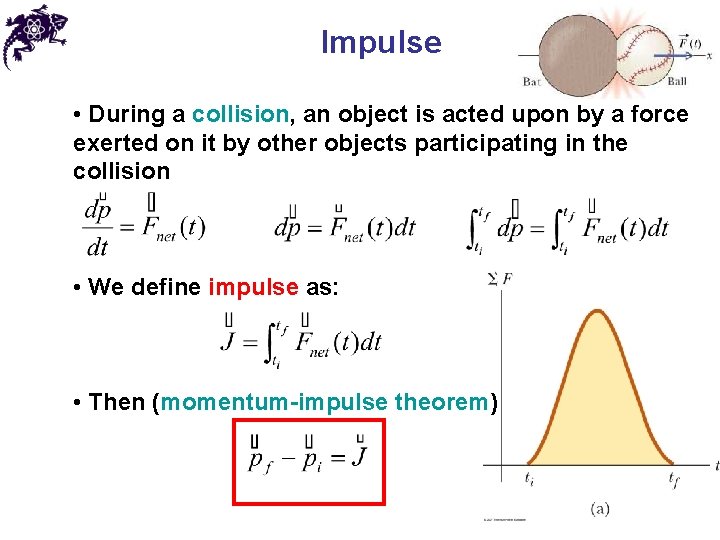
Impulse • During a collision, an object is acted upon by a force exerted on it by other objects participating in the collision • We define impulse as: • Then (momentum-impulse theorem)

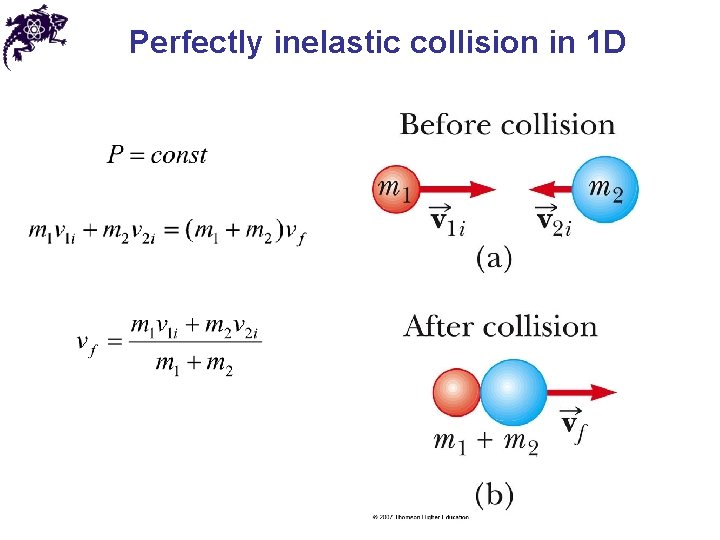
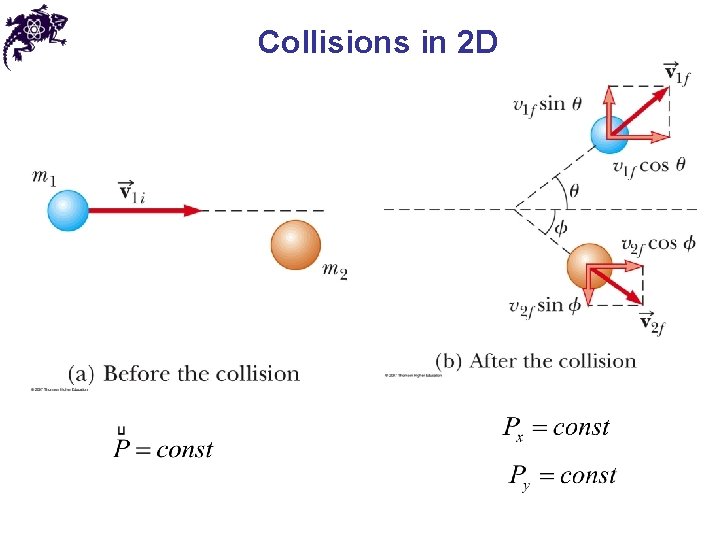
Elastic and inelastic collisions • During a collision, the total linear momentum is always conserved if the system is isolated (no external force) • It may not necessarily apply to the total kinetic energy • If the total kinetic energy is conserved during the collision, then such a collision is called elastic • If the total kinetic energy is not conserved during the collision, then such a collision is called inelastic • If the total kinetic energy loss during the collision is a maximum (the objects stick together), then such a collision is called perfectly inelastic

Elastic collision in 1 D

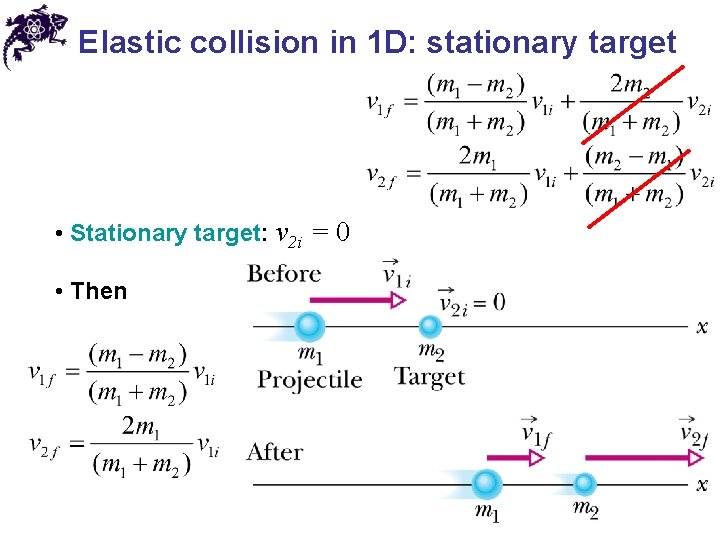
Elastic collision in 1 D: stationary target • Stationary target: v 2 i = 0 • Then

Perfectly inelastic collision in 1 D

Collisions in 2 D

Chapter 9 Problem 86 In a ballistic pendulum demonstration gone bad, a 0. 52 -g pellet, fired horizontally with kinetic energy 3. 25 J, passes straight through a 400 -g Styrofoam pendulum block. If the pendulum rises a maximum height of 0. 50 mm, how much kinetic energy did the pellet have after emerging from the Styrofoam?

Questions?

Answers to the even-numbered problems Chapter 9 Problem 12 2. 5 m

Answers to the even-numbered problems Chapter 9 Problem 16 4680 km

Answers to the even-numbered problems Chapter 9 Problem 18 – 10. 6 iˆ – 2. 8 jˆ m/s

Answers to the even-numbered problems Chapter 9 Problem 78 7. 95 s