Chapter 9 Jointly Distributed Random Variables Independence and

Chapter 9: Jointly Distributed Random Variables; Independence and Conditioning The most misleading assumptions are the ones you don’t even know you’re making. Douglas Adams and Mark Carwardine http: //math. stackexchange. com/questions/314072/joint-probability-mass-function 1

Joint PMF: Example Suppose that 15 percent of the 300 families in a certain community have no children, 20 percent have 1 child, 35 percent have 2 children, and 30 percent have 3 children. Further suppose that in each family, each child is equally likely (independent) to be a boy or a girl. Let B be the number of boys in a family chosen randomly from this community and G be the number of girls. The following is the table for this situation. 2
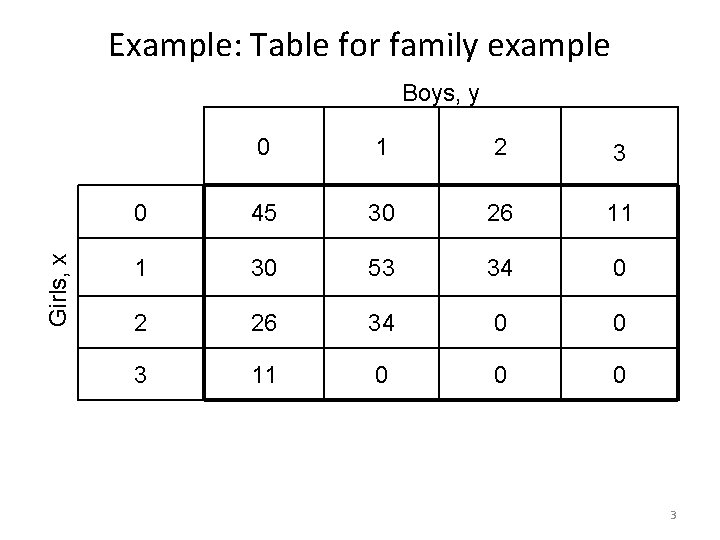
Example: Table for family example Girls, x Boys, y 0 1 2 3 0 45 30 26 11 1 30 53 34 0 2 26 34 0 0 3 11 0 0 0 3
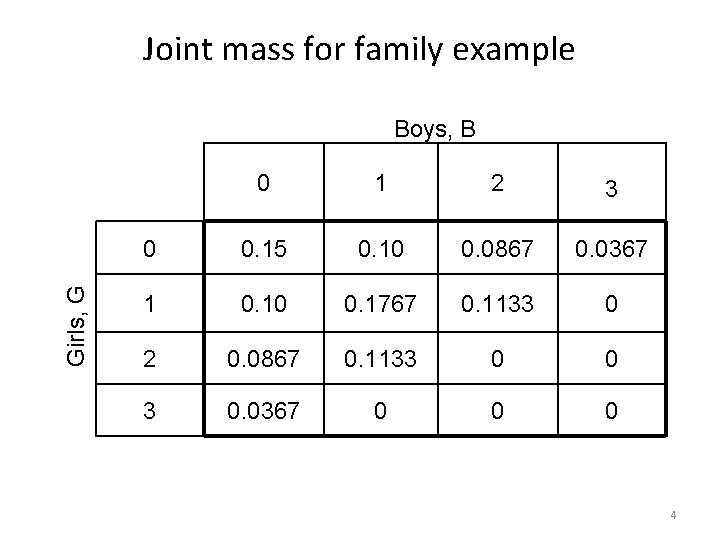
Joint mass for family example Girls, G Boys, B 0 1 2 3 0 0. 15 0. 10 0. 0867 0. 0367 1 0. 10 0. 1767 0. 1133 0 2 0. 0867 0. 1133 0 0 3 0. 0367 0 0 0 4
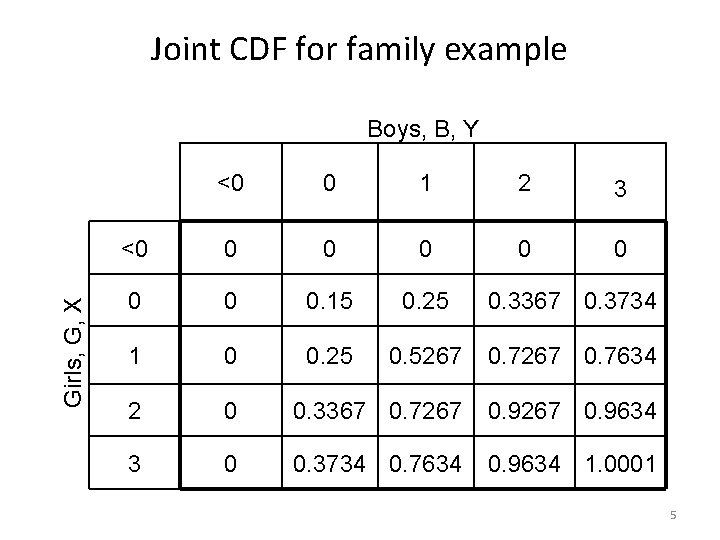
Joint CDF for family example Girls, G, X Boys, B, Y <0 0 1 2 3 <0 0 0 0 0. 15 0. 25 0. 3367 0. 3734 1 0 0. 25 0. 5267 0. 7634 2 0 0. 3367 0. 7267 0. 9634 3 0 0. 3734 0. 7634 0. 9634 1. 0001 5
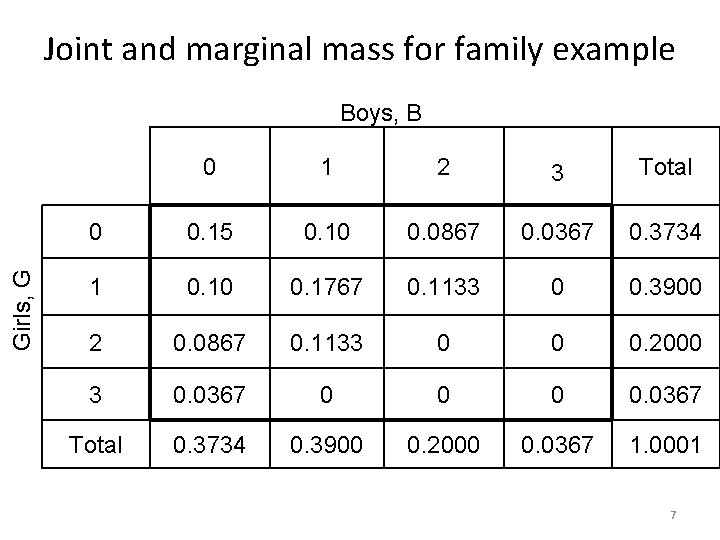
Joint and marginal mass for family example Girls, G Boys, B 0 1 2 3 Total 0 0. 15 0. 10 0. 0867 0. 0367 0. 3734 1 0. 10 0. 1767 0. 1133 0 0. 3900 2 0. 0867 0. 1133 0 0 0. 2000 3 0. 0367 0 0. 0367 Total 0. 3734 0. 3900 0. 2000 0. 0367 1. 0001 7
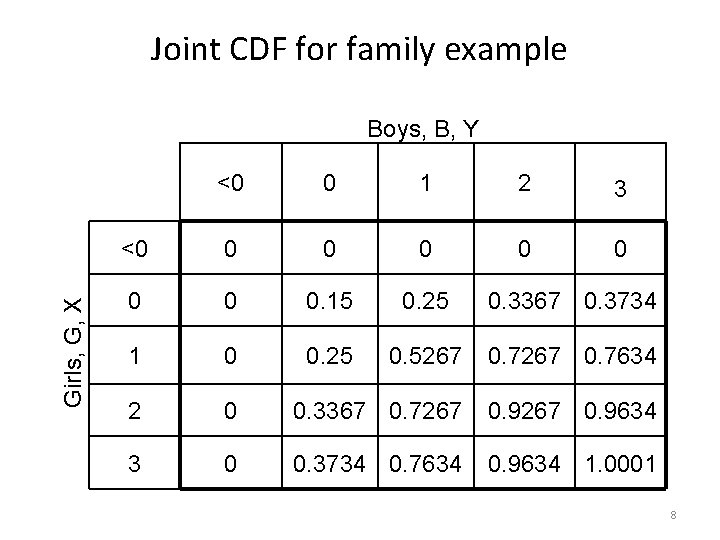
Joint CDF for family example Girls, G, X Boys, B, Y <0 0 1 2 3 <0 0 0 0 0. 15 0. 25 0. 3367 0. 3734 1 0 0. 25 0. 5267 0. 7634 2 0 0. 3367 0. 7267 0. 9634 3 0 0. 3734 0. 7634 0. 9634 1. 0001 8
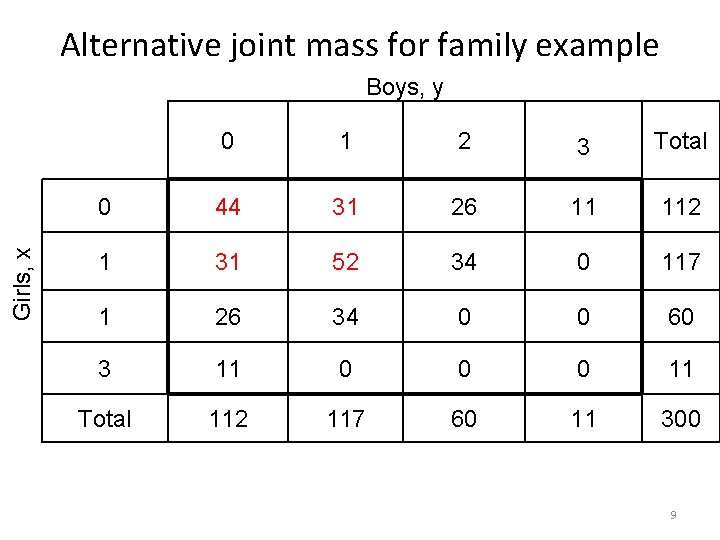
Alternative joint mass for family example Girls, x Boys, y 0 1 2 3 Total 0 44 31 26 11 112 1 31 52 34 0 117 1 26 34 0 0 60 3 11 0 0 0 11 Total 112 117 60 11 300 9
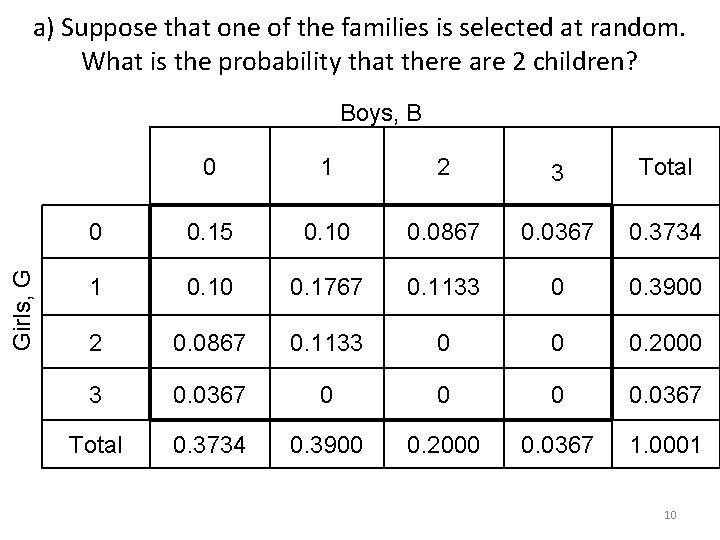
a) Suppose that one of the families is selected at random. What is the probability that there are 2 children? Girls, G Boys, B 0 1 2 3 Total 0 0. 15 0. 10 0. 0867 0. 0367 0. 3734 1 0. 10 0. 1767 0. 1133 0 0. 3900 2 0. 0867 0. 1133 0 0 0. 2000 3 0. 0367 0 0. 0367 Total 0. 3734 0. 3900 0. 2000 0. 0367 1. 0001 10
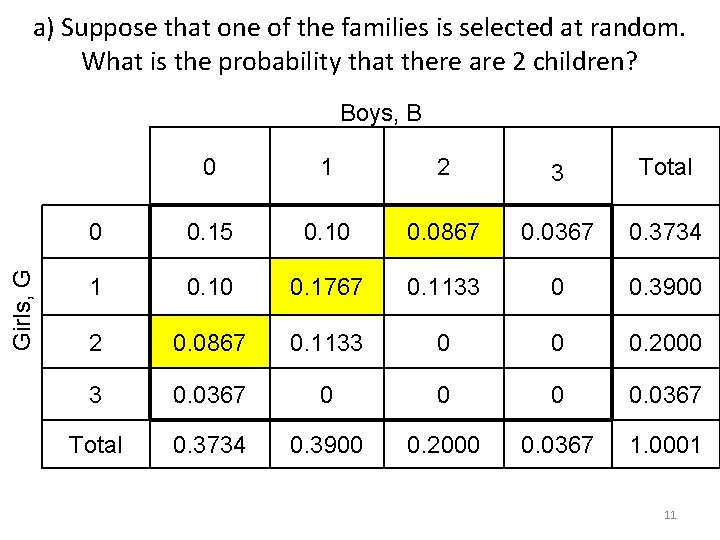
a) Suppose that one of the families is selected at random. What is the probability that there are 2 children? Girls, G Boys, B 0 1 2 3 Total 0 0. 15 0. 10 0. 0867 0. 0367 0. 3734 1 0. 10 0. 1767 0. 1133 0 0. 3900 2 0. 0867 0. 1133 0 0 0. 2000 3 0. 0367 0 0. 0367 Total 0. 3734 0. 3900 0. 2000 0. 0367 1. 0001 11
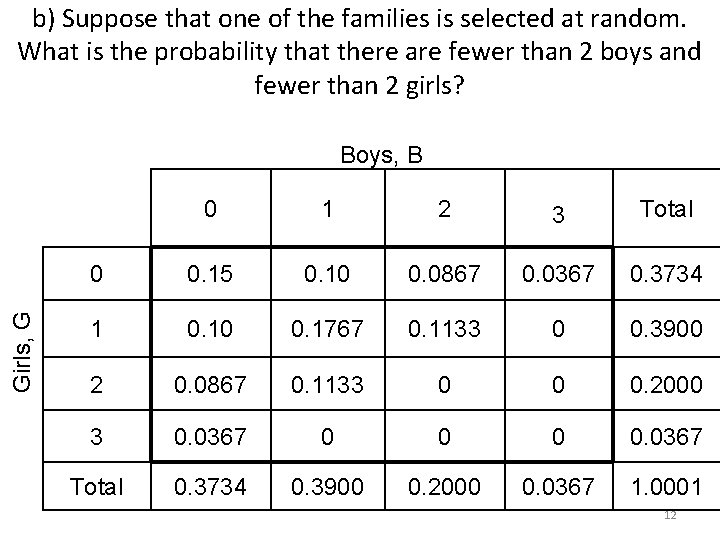
b) Suppose that one of the families is selected at random. What is the probability that there are fewer than 2 boys and fewer than 2 girls? Girls, G Boys, B 0 1 2 3 Total 0 0. 15 0. 10 0. 0867 0. 0367 0. 3734 1 0. 10 0. 1767 0. 1133 0 0. 3900 2 0. 0867 0. 1133 0 0 0. 2000 3 0. 0367 0 0. 0367 Total 0. 3734 0. 3900 0. 2000 0. 0367 1. 0001 12
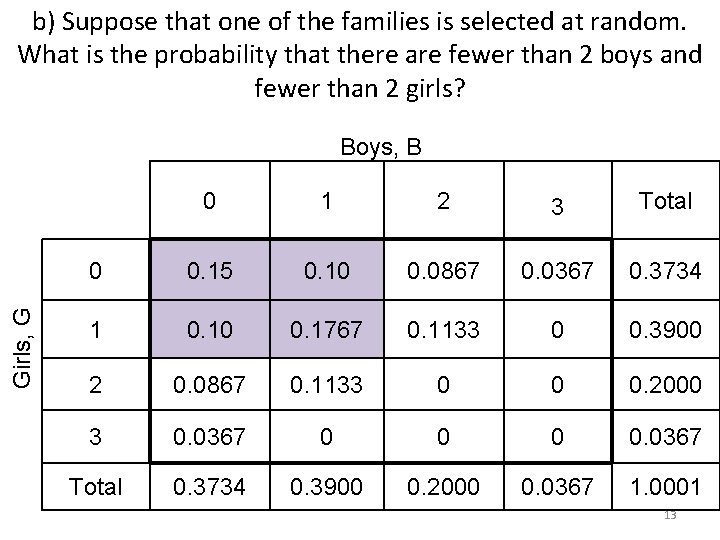
b) Suppose that one of the families is selected at random. What is the probability that there are fewer than 2 boys and fewer than 2 girls? Girls, G Boys, B 0 1 2 3 Total 0 0. 15 0. 10 0. 0867 0. 0367 0. 3734 1 0. 10 0. 1767 0. 1133 0 0. 3900 2 0. 0867 0. 1133 0 0 0. 2000 3 0. 0367 0 0. 0367 Total 0. 3734 0. 3900 0. 2000 0. 0367 1. 0001 13

Joint CDF for family example Girls, G, X Boys, B, Y <0 0 1 2 3 <0 0 0 0 0. 15 0. 25 0. 3367 0. 3734 1 0 0. 25 0. 5267 0. 7634 2 0 0. 3367 0. 7267 0. 9634 3 0 0. 3734 0. 7634 0. 9634 1. 0001 a) What is the probability that there are fewer than 2 boys and fewer than 2 girls? 14

Joint CDF for family example Girls, G, X Boys, B, Y <0 0 1 2 3 <0 0 0 0 0. 15 0. 25 0. 3367 0. 3734 1 0 0. 25 0. 5267 0. 7634 2 0 0. 3367 0. 7267 0. 9634 3 0 0. 3734 0. 7634 0. 9634 1. 0001 b) What is the probability that there are greater than 0 and at most 2 girls and greater than 0 and at most 2 boys? 15
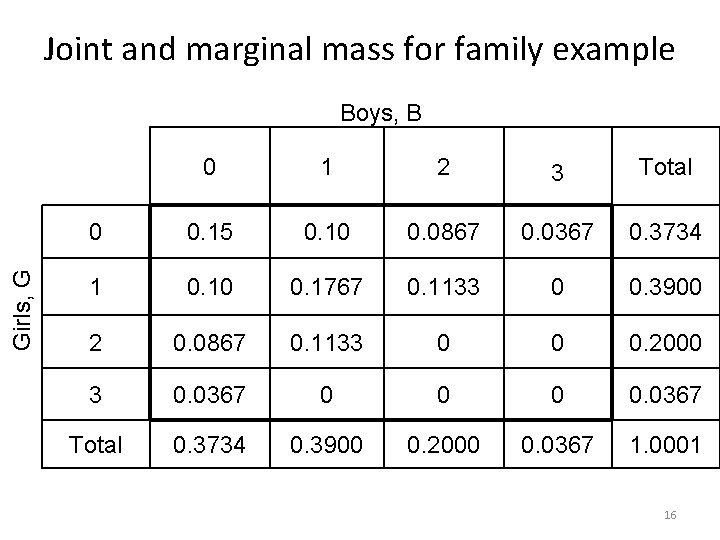
Joint and marginal mass for family example Girls, G Boys, B 0 1 2 3 Total 0 0. 15 0. 10 0. 0867 0. 0367 0. 3734 1 0. 10 0. 1767 0. 1133 0 0. 3900 2 0. 0867 0. 1133 0 0 0. 2000 3 0. 0367 0 0. 0367 Total 0. 3734 0. 3900 0. 2000 0. 0367 1. 0001 16
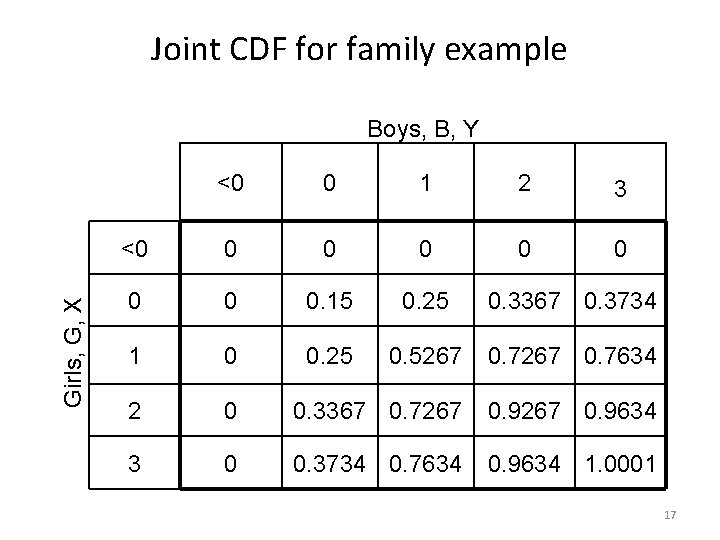
Joint CDF for family example Girls, G, X Boys, B, Y <0 0 1 2 3 <0 0 0 0 0. 15 0. 25 0. 3367 0. 3734 1 0 0. 25 0. 5267 0. 7634 2 0 0. 3367 0. 7267 0. 9634 3 0 0. 3734 0. 7634 0. 9634 1. 0001 17

Example 9. 12: Independence Roll a 4 -sided die and flip a fair coin. Let X be the result of the die roll. Let Y be 1 if the coin shows a “head” or 0 if the coin shows a “tails”. Are X and Y independent? 18

Independence of 3 or more random variables • 19

Example: Conditional mass: X (Boys) and Y (Girls) Girls, G Boys, B 0 1 2 3 p. X(x) 0 0. 15 0. 10 0. 0867 0. 0367 0. 3734 1 0. 10 0. 1767 0. 1133 0 0. 3900 2 0. 0867 0. 1133 0 0 0. 2000 3 0. 0367 0 0. 0367 p. Y(y) 0. 3734 0. 3900 0. 2000 0. 0367 1. 0001 20
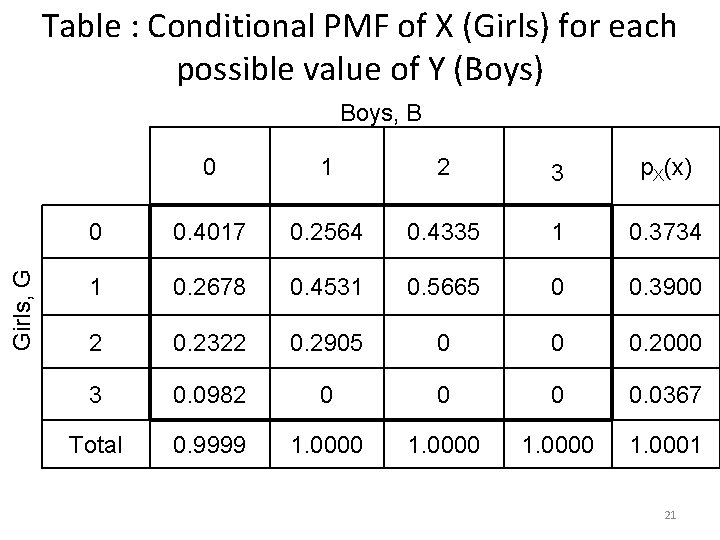
Table : Conditional PMF of X (Girls) for each possible value of Y (Boys) Girls, G Boys, B 0 1 2 3 p. X(x) 0 0. 4017 0. 2564 0. 4335 1 0. 3734 1 0. 2678 0. 4531 0. 5665 0 0. 3900 2 0. 2322 0. 2905 0 0 0. 2000 3 0. 0982 0 0. 0367 Total 0. 9999 1. 0000 1. 0001 21
- Slides: 20