Chapter 9 Inferences Based on Two Samples Confidence

Chapter 9 Inferences Based on Two Samples: Confidence Intervals and Tests of Hypothesis

Comparing Two Population Means: Independent Sampling Confidence Intervals and hypothesis testing can be done for both large and small samples Large sample cases use z-statistic, small sample cases use t-statistic When comparing two population means, we test the difference between the means

Comparing Two Population Means: Independent Sampling Large Sample Confidence Interval for 1 - 2 assuming independent sampling, which provides the following substitution

Comparing Two Population Means: Independent Sampling Properties of the Sampling Distribution of (x 1 -x 2) • Mean of Sampling distribution (x 1 -x 2) is ( 1 - 2) • Assuming two samples are independent, the standard deviation of the sampling distribution is • The sampling distribution of (x 1 -x 2) is approximately normal for large samples by the CLT

Comparing Two Population Means: Independent Sampling Large Sample Test of Hypothesis for 1 - 2

Comparing Two Population Means: Independent Sampling Required conditions for Valid Large-Sample Inferences about 1 - 2 1. Random, independent sample selection 2. Sample sizes are both at least 30 to guarantee that the CLT applies to the distribution of x 1 -x 2

Comparing Two Population Means: Independent Sampling Small Sample Confidence Interval for 1 - 2 where and t /2 is based on (n 1 +n 2 -2) degrees of freedom

Comparing Two Population Means: Independent Sampling Small Sample Test of Hypothesis for 1 - 2

Comparing Two Population Means: Independent Sampling Required conditions for Valid Small-Sample Inferences about 1 - 2 1. Random, independent sample selection 2. Approximate normal distribution of both sampled populations 3. Population variances are equal

Comparing Two Population Means: Independent Sampling Small Samples – what to do when When sample sizes are equal (n 1=n 2=n) Confidence interval: Test Statistic for H 0: where t is based on degrees of freedom

Comparing Two Population Means: Independent Sampling Small Samples – what to do when When sample sizes are not equal (n 1 n 2) Confidence interval: Test Statistic for H 0: where t is based on degrees of freedom

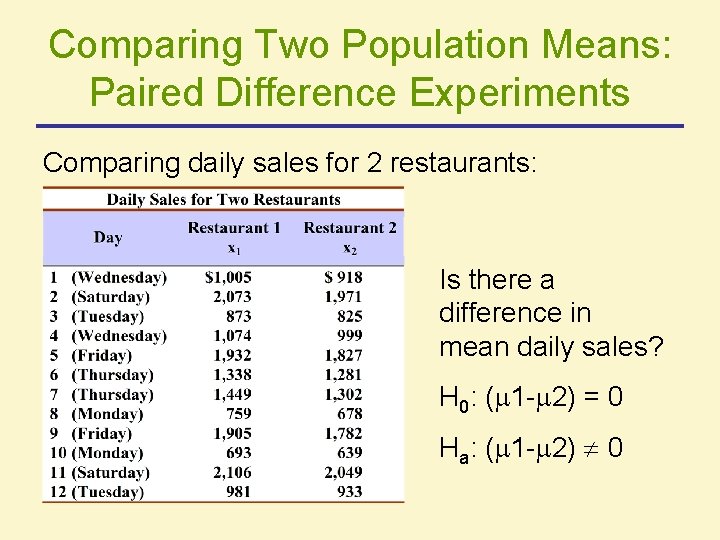
Comparing Two Population Means: Paired Difference Experiments Comparing daily sales for 2 restaurants: Is there a difference in mean daily sales? H 0: ( 1 - 2) = 0 Ha: ( 1 - 2) 0

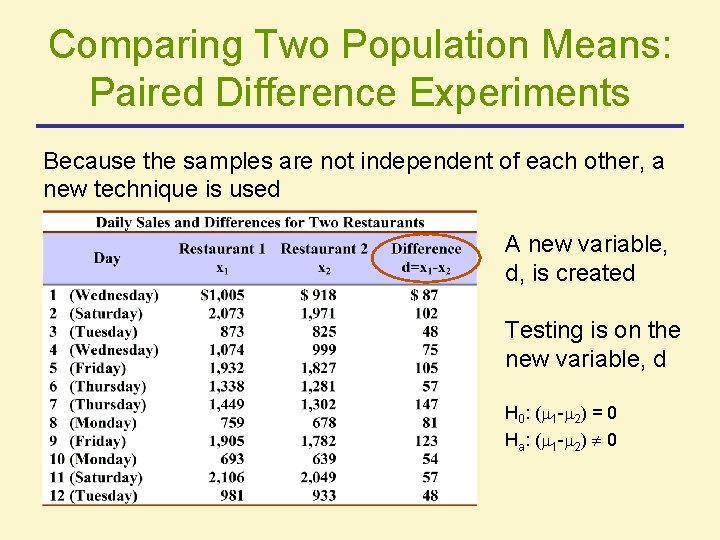
Comparing Two Population Means: Paired Difference Experiments Because the samples are not independent of each other, a new technique is used A new variable, d, is created Testing is on the new variable, d H 0: ( 1 - 2) = 0 Ha: ( 1 - 2) 0

Comparing Two Population Means: Paired Difference Experiments Testing is now based on a one sample tstatistic where = Sample mean difference sd = Sample standard deviation of differences nd = Number of differences (number of pairs)

Comparing Two Population Means: Paired Difference Experiments • This type of experiment (paired observations) is called a paired difference experiment • Pairing removes differences between pairs (days in this case), focuses on differences within pairs (sales) • Comparisons within groups is called blocking • Paired difference experiment is a randomized block experiment

Comparing Two Population Means: Paired Difference Experiments Paired Difference Confidence Interval for d= 1 - 2 Large Sample Small Sample where t /2 is based on (nd-1) degrees of freedom

Comparing Two Population Means: Paired Difference Experiments Paired Difference Test of Hypothesis for d= 1 - 2, Large Sample

Comparing Two Population Means: Paired Difference Experiments Paired Difference Test of Hypothesis for d= 1 - 2, Small Sample

Comparing Two Population Means: Paired Difference Experiments Conditions for Valid Large-Sample Inferences about d 1. Random sample of differences selected 2. Sample size is large (nd > 30) Conditions for Valid Small-Sample Inferences about d 1. Random sample of differences selected 2. Population of differences has a distribution that is approximately normal

Comparing Two Population Proportions: Independent Sampling Properties of the Sampling Distribution of • Mean of Sampling distribution • of ; is an unbiased estimator • Standard deviation of sampling distribution of • If n 1 and n 2 are large, the sampling distribution of is approximately normal is

Comparing Two Population Proportions: Independent Sampling Large-Sample 100(1 - )% Confidence Interval for (p 1 -p 2)

Comparing Two Population Proportions: Independent Sampling Conditions required for Valid Large-Sample Inferences about (p 1 -p 2) • Independent, randomly selected samples • Sample sizes n 1 and n 2 are sufficiently large so that the sampling distribution of will be approximately normal.

Comparing Two Population Proportions: Independent Sampling Large-Sample Test of Hypothesis about (p 1 -p 2)

Determining the Sample Size For estimating 1 - 2 (assuming n 1=n 2=n) Given , a margin of error ME and an estimate of , solve for

Determining the Sample Size For estimating p 1 -p 2 (assuming n 1=n 2=n) Given , a margin of error ME and an estimate of , solve for

Comparing Two Population Variances: Independent Sampling • Technique used when you want to compare the variability of two populations • Based on inference about the ratio of variances or • Test statistic used is • Sampling distribution of test statistic F follows the F-Distribution

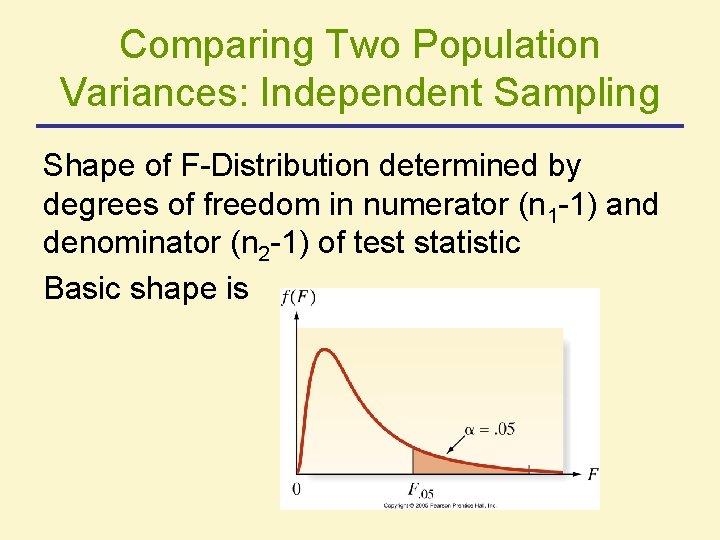
Comparing Two Population Variances: Independent Sampling Shape of F-Distribution determined by degrees of freedom in numerator (n 1 -1) and denominator (n 2 -1) of test statistic Basic shape is

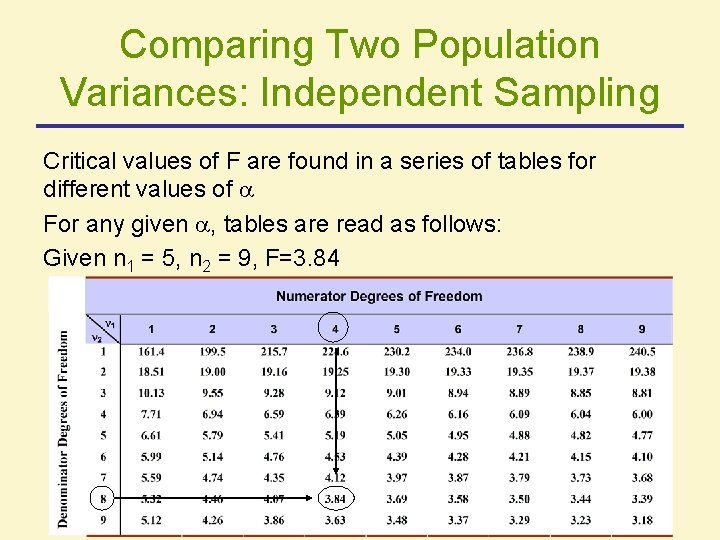
Comparing Two Population Variances: Independent Sampling Critical values of F are found in a series of tables for different values of For any given , tables are read as follows: Given n 1 = 5, n 2 = 9, F=3. 84

Comparing Two Population Variances: Independent Sampling F-Test for Equal Population Variances

Comparing Two Population Variances: Independent Sampling Required Conditions for a Valid F-Test for Equal Variances • Both sampled populations are normally distributed • Random, independent samples are drawn